Cho các điểm phân biệt \(A,B,C\). Đẳng thức nào sau đây đúng ?
\(\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {AC} \).
Cho 3 điểm$A,{\rm{ }}B,{\rm{ }}C$. Đẳng thức nào sau đây đúng.
Ta có: $\overrightarrow {AB} = \overrightarrow {CB} - \overrightarrow {CA} $ (qui tắc 3 điểm).
Cho hình bình hành \(ABCD\),với giao điểm hai đường chéo là \(I\). Khi đó:
Ta có: \(\overrightarrow {AB} + \overrightarrow {IA} = \overrightarrow {IB}\ne \overrightarrow {BI} \) nên A sai.
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}\ne \overrightarrow {BD}\) nên B sai.
\(\overrightarrow {AB} + \overrightarrow {CD} =\overrightarrow {AB} + \overrightarrow {BA}= \vec 0\) nên C đúng.
Cho $4$ điểm bất kì $A,B,C,O$. Đẳng thức nào sau đây đúng?
Theo qui tắc $3$ điểm ta có: $\overrightarrow {OA} = \overrightarrow {CA} - \overrightarrow {CO} $.
Chọn khẳng định đúng :
Nếu \(G\) là trọng tâm tam giác \(ABC\) thì \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0\).
Chọn khẳng định sai:
Ta có: $\overrightarrow {IA} - \overrightarrow {IB} = \overrightarrow {BA} \ne \overrightarrow 0 $ nên A sai.
Chọn khẳng định sai
Nếu \(I\) là trung điểm đoạn \(AB\) thì \(\overrightarrow {IA} + \overrightarrow {BI} = \vec 0\).
Vì \(\overrightarrow {IA} + \overrightarrow {BI} = \overrightarrow {BI} + \overrightarrow {IA} = \overrightarrow {BA} \ne \vec 0\) nên A sai.
Cho hình vuông $ABCD$ cạnh $a$, tâm $O$. Khi đó: $\left| {\overrightarrow {OA} - \overrightarrow {BO} } \right| = $
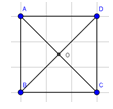
Ta có: $\left| {\overrightarrow {OA} - \overrightarrow {BO} } \right| = \left| {\overrightarrow {CO} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {CB} } \right| = a$.
Cho hình bình hành \(ABCD\) tâm \(O\). Khi đó \(\overrightarrow {OA} + \overrightarrow {BO} = \)
Ta có: \(\overrightarrow {OA} + \overrightarrow {BO} = \overrightarrow {BA} = \overrightarrow {CD} \).
Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác vectơ – không. Trong đó hai vectơ $\overrightarrow a ,\overrightarrow b $ cùng hướng, hai vectơ $\overrightarrow a \,,{\rm{ }}\overrightarrow c $ đối nhau. Khẳng định nào sau đây đúng ?
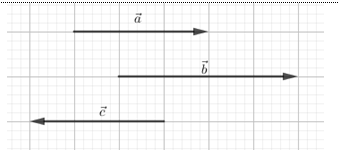
Quan sát hình vẽ trên ta thấy hai vectơ $\overrightarrow b ,\overrightarrow c $ ngược hướng.
Cho tam giác đều $ABC$ cạnh $a$. Khi đó $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = $

Dựng hình bình hành \(ABDC\) và gọi \(M\) là trung điểm của \(BC\).
Ta có: $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = 2AM$
Trong tam giác đều \(ABC\) có \(AM\) là trung tuyến cũng là đường cao nên \(AM \bot BC,MB = MC = \dfrac{a}{2}\)
Ta có:
\(A{M^2} + M{B^2} = A{B^2}\) \( \Leftrightarrow A{M^2} + {\left( {\dfrac{a}{2}} \right)^2} = {a^2}\) \( \Leftrightarrow A{M^2} = {a^2} - \dfrac{{{a^2}}}{4}\) \( \Leftrightarrow A{M^2} = \dfrac{{3{a^2}}}{4}\) \( \Leftrightarrow AM = \dfrac{{a\sqrt 3 }}{2}\)
Vậy \(AD = 2AM = 2.\dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \)
Cho hình chữ nhật $ABCD$ biết $AB = 4a$ và $AD = 3a$ thì độ dài \(\overrightarrow {AB} + \overrightarrow {AD} \) là:
Áp dụng quy tắc hình bình hành ta có:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) \( \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
\(A{C^2} = A{B^2} + B{C^2}\) \( = {\left( {4a} \right)^2} + {\left( {3a} \right)^2} = {\left( {5a} \right)^2}\) \( \Rightarrow AC = 5a\)
Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 5a\)

Gọi $G$ là trọng tâm tam giác vuông $ABC\;$ với cạnh huyền $BC = 12$. Vectơ $\overrightarrow {GB} - \overrightarrow {CG} $ có độ dài bằng bao nhiêu?

Ta có: $\overrightarrow {GB} - \overrightarrow {CG} = \overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GE} = \dfrac{2}{3}\overrightarrow {AE} $ (Vì \(\overrightarrow {GE} = \dfrac{1}{3}\overrightarrow {AE} \)).
$ \Rightarrow \left| {\overrightarrow {GB} - \overrightarrow {CG} } \right| = \dfrac{2}{3}\left| {\overrightarrow {AE} } \right| = \dfrac{2}{3}.\dfrac{{BC}}{2} = \dfrac{{BC}}{3} = 4$
Cho 6 điểm $A,B,C,D,E,F$. Đẳng thức nào sau đây đúng.
Ta có:
$\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FA} + \overrightarrow {BC} + \overrightarrow {EF} + \overrightarrow {DE} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DE} + \overrightarrow {EF} + \overrightarrow {FA} = \overrightarrow 0 $
Cho tam giác đều $ABC$ cạnh \(a\), gọi $G$ là trọng tâm. Khi đó giá trị $\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right|$ là:

Ta có:
$\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right| = \left| {\overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {CG} } \right| = \left| {\overrightarrow {AG} + \overrightarrow {CB} } \right| = \left| {2\overrightarrow {GH} + 2\overrightarrow {HB} } \right|$
$ = 2\left| {\overrightarrow {GH} + \overrightarrow {HB} } \right| = 2\left| {\overrightarrow {GB} } \right| = 2GB = 2GA = 2.\dfrac{2}{3}AH = \dfrac{4}{3} .\dfrac{a\sqrt 3}{2}= \dfrac{{2a\sqrt 3 }}{3}$.
Gọi \(G\) là trọng tâm tam giác vuông$ABC$với cạnh huyền $BC = 12$. Tổng hai vectơ $\overrightarrow {GB} + \overrightarrow {GC} $ có độ dài bằng bao nhiêu ?

Dựng hình bình hành \(GBDC\). Gọi \(M\) là trung điểm \(BC\).
Tam giác \(ABC\) có trung tuyến \(AM\) nên \(AM = \dfrac{1}{2}BC = \dfrac{1}{2}.12 = 6\)
\( \Rightarrow GM = \dfrac{1}{3}AM = \dfrac{1}{3}.6 = 2\) \( \Rightarrow GD = 2GM = 2.2 = 4\)
Vậy \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {\overrightarrow {GD} } \right| = GD = 4\)
Chỉ ra vectơ tổng \(\overrightarrow {MN} - \overrightarrow {QP} + \overrightarrow {RN} - \overrightarrow {PN} + \overrightarrow {QR} \) trong các vectơ sau:
Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PQ} + \overrightarrow {QR} + \overrightarrow {RN} = \overrightarrow {MN} \).
Cho hình thoi $ABCD$ tâm $O$, cạnh bằng \(a\) và góc \(A\) bằng \({60^0}\). Kết luận nào sau đây đúng:

Do \(AB = AD\) và \(\widehat A = {60^0}\) nên tam giác \(ABD\) đều.
Do đó $\left| {\overrightarrow {OA} } \right| = OA = \sqrt {A{B^2} - B{O^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}$
Cho bốn điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D$ phân biệt. Khi đó vectơ \(\overrightarrow u = \overrightarrow {AD} - \overrightarrow {CD} + \overrightarrow {CB} - \overrightarrow {AB} \) bằng:
Ta có: \(\overrightarrow u = \overrightarrow {AD} - \overrightarrow {CD} + \overrightarrow {CB} - \overrightarrow {AB} = \overrightarrow {AD} - \overrightarrow {AB} + \overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {BD} + \overrightarrow {DB} = \overrightarrow 0 \)
Cho tam giác $ABC$. Gọi $M,N,P$ lần lượt là trung điểm các cạnh $AB,AC,BC$. Hỏi $\overrightarrow {MP} + \overrightarrow {NP} $ bằng vec tơ nào?

Vì $ANPM$ là hình bình hành nên theo quy tắc hình bình hành ta có: $\overrightarrow {MP} + \overrightarrow {NP} = \overrightarrow {AN} + \overrightarrow {AM} = \overrightarrow {AP} $

