Gọi $B$ là trung điểm của đoạn thẳng $AC$. Đẳng thức nào sau đây là đúng?

Ta có: \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow 0 \).
Cho hình vuông $ABCD$ cạnh $a$, tâm $O$. Khi đó: $\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = $

Dựng hình bình hành \(OAEB\) và gọi \(M\) là giao điểm của \(AB\) và \(OE\).
Ta có: $\left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {OE} } \right| = OE = 2OM = a$
Cho tam giác \(ABC\), trọng tâm là \(G\). Phát biểu nào là đúng?
Ta có: $\left| {\overrightarrow {GA} - \overrightarrow {BG} - \overrightarrow {CG} } \right| = \left| {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {\overrightarrow 0 } \right| = 0$.
Cho lục giác đều$ABCDEF$ và \(O\) là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
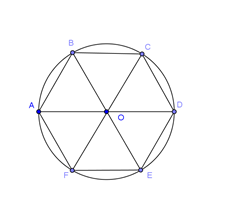
$\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FE} = \overrightarrow {AB} + \overrightarrow {BO} + \overrightarrow {FE} = \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {AD} \ne \overrightarrow 0 $.
Cho tam giác \(ABC\). Để điểm \(M\) thoả mãn điều kiện \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) thì \(M\) phải thỏa mãn mệnh đề nào?
Ta có: \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
Vậy: \(M\) là điểm sao cho tứ giác \(BAMC\)là hình bình hành.
Cho \(\Delta ABC\) vuông tại \(A\) và \(AB = 3\), \(AC = 4\). Véctơ \(\overrightarrow {CB} + \overrightarrow {AB} \) có độ dài bằng
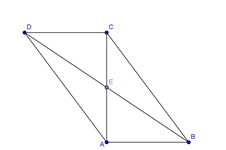
Dựng hình bình hành \(ABCD\) tâm \(E\)
Ta có: \(\overrightarrow {CB} + \overrightarrow {AB} = \overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow {CB} + \overrightarrow {AB} } \right| = \left| {\overrightarrow {DB} } \right| = DB = 2EB = 2\sqrt {A{E^2} + A{B^2}} = 2\sqrt {13} \)
Cho tam giác \(ABC\). Để điểm \(M\) thoả mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow 0 \) thì \(M\) phải thỏa mãn mệnh đề nào?
$\overrightarrow {MA} + \overrightarrow {BM} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MA} + \overrightarrow {BC} = \vec 0 \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AM} $
Vậy \(M\) là điểm sao cho tứ giác \(BAMC\)là hình bình hành.
Cho hình thang $ABCD$ có \(AB\) song song với \(CD\). Cho $AB = 2a;CD = a$. Gọi \(O\) là trung điểm của \(AD\). Khi đó :
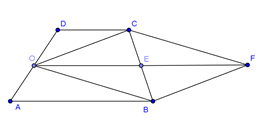
Dựng hình bình hành \(OBFC\) tâm \(E\). Khi đó
$\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = \left| {\overrightarrow {OF} } \right| = OF = 2OE = AB + CD = 3a$.
Cho tam giác $ABC$. Tập hợp những điểm \(M\) sao cho: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MB} } \right|\) là:
Gọi\(I,J\) lần lượt là trung điểm của \(AB\) và\(BC\). Khi đó:
\(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC} + \overrightarrow {MB} } \right| \Leftrightarrow 2\left| {\overrightarrow {MI} } \right| = 2\left| {\overrightarrow {MJ} } \right| \Leftrightarrow MI = MJ\)
Vậy \(M\) nằm trên đường trung trực của \(IJ\).
Chú ý khi giải:
Một số em có thể sẽ chọn nhầm đáp án A sau khi có đẳng thức độ dài \(MI = MJ\) là sai.

