Trả lời bởi giáo viên
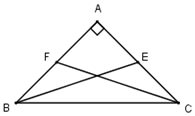
Gọi a là góc tạo bởi hai trung tuyến BE,CF.
Khi đó $\cos a = \dfrac{{\left| {\overrightarrow {BE} .\overrightarrow {CF} } \right|}}{{\left| {\overrightarrow {BE} } \right|\left| {\overrightarrow {CF} } \right|}}$
Sử dụng phân tích
$\begin{array}{l}\overrightarrow {BE} .\overrightarrow {CF} = \left( {\overrightarrow {BA} + \overrightarrow {AE} } \right)\left( {\overrightarrow {CA} + \overrightarrow {AF} } \right)\\ = \overrightarrow {BA} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AF} + \overrightarrow {AE} .\overrightarrow {CA} + \overrightarrow {AE} .\overrightarrow {AF} \\ = 0 - \overrightarrow {AB} .\dfrac{{\overrightarrow {AB} }}{2} - \overrightarrow {AC} \dfrac{{\overrightarrow {AC} }}{2} + 0\\ = - \dfrac{{A{B^2}}}{2} - \dfrac{{A{C^2}}}{2} = - \dfrac{{A{B^2}}}{2} - \dfrac{{A{B^2}}}{2} = - A{B^2}.\end{array}$
$BE = CF = \sqrt {A{B^2} + A{E^2}} = \sqrt {A{B^2} + \dfrac{{A{B^2}}}{4}} = AB\sqrt {\dfrac{5}{4}} $
Từ đó suy ra $\cos a = \dfrac{{A{B^2}}}{{A{B^2}\dfrac{5}{4}}} = \dfrac{4}{5}.$
Hướng dẫn giải:
Sử dụng công thức tính góc giữa hai vector:$\cos a = \dfrac{{\left| {\overrightarrow {BE} .\overrightarrow {CF} } \right|}}{{\left| {\overrightarrow {BE} } \right|\left| {\overrightarrow {CF} } \right|}}$ , phân tích biểu thức tích vô hướng về dạng đặc biệt.

