Cho sơ đồ mạch điện như sau. Biết rằng R = R1 = R2 = 5 Ω. Hãy tính các cường độ dòng điện I, I1 và I2.

Trả lời bởi giáo viên
A. \(I = \dfrac{8}{{15}},{I_2} = \dfrac{4}{{15}},{I_3} = \dfrac{4}{{15}}.\)
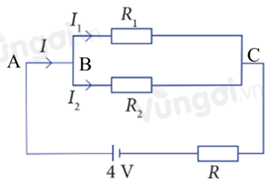
Tổng cường độ dòng điện ra vào vào tại điểm B bằng nhau nên ta có I = I1 + I2 (1).
Hiệu điện thế giữa hai điểm A và C được tính bởi:
UAC = IR + I1R1 = 5I + 5I1 suy ra 5I + 5I1 = 4 (2).
Hiệu điện thế giữa hai điểm B và C được tính bởi:
UBC = I1R1 = I2R2 suy ra 5I1 = 5I2 hay I1 = I2 (3).
Từ (1), (2) và (3) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{I - {I_1} - {I_2} = 0,5}\\{5I + 5{I_1} = 4}\\{{I_1} - {I_2} = 0}\end{array}} \right.\)
Giải hệ này ta được \(I = \dfrac{8}{{15}},{I_2} = \dfrac{4}{{15}},{I_3} = \dfrac{4}{{15}}.\)
Hướng dẫn giải:
Tổng cường độ dòng điện ra vào vào tại điểm B bằng nhau.
UAC = IR + I1R1
UBC = I1R1 = I2R2
=>Từ đó lập hệ phương trình bậc nhất ba ẩn.



