Trong mặt phẳng với hệ tọa độ \(Oxy\), cho các điểm \(A,B,C,M,N,P\) như hình vẽ.
Điểm nào dưới đây thuộc đường tròn ngoại tiếp tam giác \(ABC\)?
Từ hình vẽ ta thấy \(A\left( { - 1;4} \right),B\left( {3; - 4} \right),C\left( {6;5} \right),\)\(M\left( { - 2;2} \right),N\left( {8;0} \right),P\left( {6; - 3} \right)\)
Gọi đường tròn ngoại tiếp tam giác ABC có dạng: \({x^2} + {y^2} + ax + by + c = 0\)
Ta có hệ: \(\left\{ \begin{array}{l}1 + 16 - a + 4b + c = 0\\9 + 16 + 3a - 4b + c = 0\\36 + 25 + 6a + 5b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - a + 4b + c = - 17\\3a - 4b + c = - 25\\6a + 5b + c = - 61\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 6\\b = - 2\\c = - 15\end{array} \right.\)
\( \Rightarrow \left( C \right):{x^2} + {y^2} - 6x - 2y - 15 = 0\)
Ta có: \(36 + 9 - 6.6 + 2.3 - 15 = 0\). Vậy \(P\left( {6; - 3} \right) \in \left( C \right)\)
Cho tam giác \(ABC\) có diện tích bằng \(S = \dfrac{3}{2}\), hai đỉnh \(A\left( {2;\; - 3} \right)\) và \(B\left( {3;\; - 2} \right)\). Trọng tâm \(G\) nằm trên đường thẳng \(3x - y - 8 = 0\). Tìm tọa độ đỉnh \(C\)?
Gọi \(G\left( {a;\;3a - 8} \right)\). Do \({S_{ABC}} = \dfrac{3}{2} \Rightarrow {S_{GAB}} = \dfrac{1}{2}\).
Đường thẳng \(AB\) nhận \(\overrightarrow {AB} = \left( {1;\;1} \right)\) là véc tơ chỉ phương nên có phương trình \(x - y - 5 = 0\).
\(AB = \sqrt 2 \), \(d\left( {G;AB} \right) = \dfrac{{\left| {a - \left( {3a - 8} \right) - 5} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{\left| {3 - 2a} \right|}}{{\sqrt 2 }}\).
Do \({S_{GAB}} = \dfrac{1}{2} \Rightarrow \dfrac{1}{2}.AB.d\left( {G;AB} \right) = \dfrac{1}{2}\)\( \Leftrightarrow \sqrt 2 .\dfrac{{\left| {3 - 2a} \right|}}{{\sqrt 2 }} = 1\)\( \Leftrightarrow \left| {3 - 2a} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}a = 1\\a = 2\end{array} \right.\).
Với \(a = 1 \Rightarrow G\left( {1;\; - 5} \right) \Rightarrow C\left( { - 2;\; - 10} \right)\).
Với \(a = 2 \Rightarrow G\left( {2;\; - 2} \right) \Rightarrow C\left( {1;\; - 1} \right)\).
Vậy $C\left( { - 2;\; - 10} \right)$ hoặc \(C\left( {1;\; - 1} \right)\) thỏa mãn yêu cầu bài toán.
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {3\,;\,4} \right)\), \(B\left( {2\,;\,1} \right)\), \(C\left( { - 1\,;\, - 2} \right)\). Gọi \(M\left( {x\,;\,y} \right)\) là điểm trên đường thẳng \(BC\) sao cho \({S_{\Delta ABC}} = 4{S_{\Delta ABM}}\). Tính \(P = x.y\).
Dễ thấy \(\dfrac{{{S_{\Delta ABC}}}}{{{S_{\Delta ABM}}}} = 4\) \( \Leftrightarrow \dfrac{{BC}}{{BM}} = 4\) \( \Leftrightarrow \left[ \begin{array}{l}\overrightarrow {BC} = 4\overrightarrow {BM} \\\overrightarrow {BC} = - 4\overrightarrow {BM} \end{array} \right.\).
TH1: \(\overrightarrow {BC} = 4\overrightarrow {BM} \) thì: \(\left\{ \begin{array}{l}x - 2 = - \dfrac{3}{4}\\y - 1 = - \dfrac{3}{4}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{5}{4}\\y = \dfrac{1}{4}\end{array} \right.\) \( \Rightarrow x.y = \dfrac{5}{{16}}\).
TH2: \(\overrightarrow {BC} = - 4\overrightarrow {BM} \) thì: \(\left\{ \begin{array}{l}x - 2 = \dfrac{3}{4}\\y - 1 = \dfrac{3}{4}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{4}\\y = \dfrac{7}{4}\end{array} \right.\) \( \Rightarrow x.y = \dfrac{{77}}{{16}}\).
Cho hai điểm \(P\left( {1;6} \right)\) và \(Q\left( { - 3; - 4} \right)\) và đường thẳng \(\Delta \): \(2x - y - 1 = 0\). Tọa độ điểm \(N\) thuộc \(\Delta \) sao cho \(\left| {NP - NQ} \right|\) lớn nhất.
Ta có: $\left( {2.1 - 6 - 1} \right).\left( { - 2.3 - 4 - 1} \right) = 55 > 0$ \( \Rightarrow P\) và \(Q\) cùng phía so với \(\Delta \).
Phương trình đường thẳng \(PQ\): \(5x - 2y + 7 = 0\).
Gọi $H = \Delta \cap PQ$, tọa độ \(H\) là nghiệm của hệ phương trình: $\left\{ \begin{array}{l}2x - y - 1 = 0\\5x - 2y + 7 = 0\end{array} \right.$ \( \Leftrightarrow \left\{ \begin{array}{l}x = - 9\\y = - 19\end{array} \right.\).
Hay \(H\left( { - 9; - 19} \right)\).
Với mọi điểm \(N \in \Delta \) thì: \(\left| {NP - NQ} \right|\) \( \le \left| {HP - HQ} \right| = \left| {PQ} \right|\) \( \Rightarrow {\left| {NP - NQ} \right|_{\max }} = \left| {PQ} \right|\).
Dấu bằng xảy ra khi \(N\) trùng \(H\).
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(I\left( {2;\;1} \right)\), trọng tâm \(G\left( {\dfrac{7}{3};\;\dfrac{4}{3}} \right)\), phương trình đường thẳng \(AB:x - y + 1 = 0\). Giả sử điểm \(C\left( {{x_0};\;{y_0}} \right)\), tính \(2{x_0} + {y_0}\).
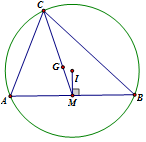
Gọi \(M\left( {a;\;a + 1} \right)\) là trung điểm \(AB\).
Ta có \(\overrightarrow {IM} = \left( {a - 2;\;a} \right)\), $1$ VTCP của $AB$ là \(\overrightarrow {{u_{AB}}} = \left( {1;\;1} \right)\).
Mà $\overrightarrow {IM} \bot \overrightarrow {{u_{AB}}} $ $ \Leftrightarrow \overrightarrow {IM} .\overrightarrow {{u_{AB}}} = 0$ \( \Leftrightarrow a - 2 + a = 0\) \( \Leftrightarrow a = 1\). Vậy \(M\left( {1;\;2} \right)\).
Nhận xét \(\overrightarrow {CG} = 2\overrightarrow {GM} \) \( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{7}{3} - {x_0} = 2\left( {1 - \dfrac{7}{3}} \right)\\\dfrac{4}{3} - {y_0} = 2\left( {2 - \dfrac{4}{3}} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_0} = 5\\{y_0} = 0\end{array} \right.\).
Vậy \(2{x_0} + {y_0} = 10\).
Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(M\left( {4;{\rm{ 1}}} \right)\), đường thẳng \(d\) qua \(M\), \(d\)cắt tia \(Ox\), \(Oy\) lần lượt tại \(A\left( {a;{\rm{ 0}}} \right)\), \(B\left( {0;{\rm{ }}b} \right)\) sao cho tam giác \(ABO\) (\(O\) là gốc tọa độ) có diện tích nhỏ nhất. Giá trị \(a - 4b\) bằng
Ta có phương trình đường thẳng \(d\) có dạng: \(\dfrac{x}{a} + \dfrac{y}{b} = 1\) (theo giả thiết ta có \(a > 0,{\mkern 1mu} b > 0\))
Do \(d\) đi qua \(M\left( {4;{\rm{ 1}}} \right)\) nên ta có \(\dfrac{4}{a} + \dfrac{1}{b} = 1\)
Mặt khác diện tích của tam giác vuông \(ABO\) là \({S_{ABO}} = \dfrac{1}{2}ab\)
Áp dụng BĐT Cô si ta có \(1 = \dfrac{4}{a} + \dfrac{1}{b} \ge 2\sqrt {\dfrac{4}{a}.\dfrac{1}{b}} = \dfrac{4}{{\sqrt {ab} }}\) \( \Leftrightarrow \sqrt {ab} \ge 4 \Leftrightarrow \dfrac{1}{2}ab \ge 8\)
Vậy diện tích của tam giác vuông \(ABO\) nhỏ nhất bằng \(8\) khi $a$, $b$ thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\dfrac{4}{a} = \dfrac{1}{b}\\\dfrac{4}{a} + \dfrac{1}{b} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 8\\b = 2\end{array} \right.\) \( \Rightarrow a - 4b = 8 - 4.2 = 0\).
Trong mặt phẳng tọa độ $Oxy$, tam giác $ABC$ có đỉnh \(A\left( { - 1;2} \right)\), trực tâm \(H\left( { - 3; - 12} \right)\), trung điểm của cạnh $BC$ là \(M\left( {4;3} \right)\). Gọi $I$, $R$ lần lượt là tâm, bán kính đường tròn ngoại tiếp tam giác $ABC$. Chọn khẳng định đúng trong các khẳng định sau
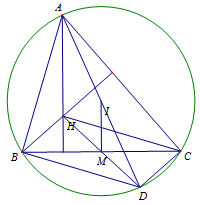
Kẻ đường kính \(AD\) của đường tròn \(\left( I \right)\) khi đó ta có \(BHCD\) là hình bình hành
\( \Rightarrow \)\(M\) là trung điểm của cạnh \(HD\).
Xét tam giác \(AHD\) có \(IM\) là đường trung bình \( \Rightarrow IM = \dfrac{1}{2}AH\) \( \Rightarrow \overrightarrow {IM} = \dfrac{1}{2}\overrightarrow {AH} \).
Gọi \(I\left( {x;y} \right)\) ta có \(\overrightarrow {IM} = \left( {4 - x;3 - y} \right)\); \(\overrightarrow {AH} = \left( { - 2; - 14} \right)\) \( \Rightarrow I\left( {5;10} \right)\).
Bán kính \(R = IA = \sqrt {{{\left( {5 + 1} \right)}^2} + {{\left( {10 - 2} \right)}^2}} = 10\)
Trong mặt phẳng với hệ trục $Oxy$, cho hình vuông \(ABCD\) có tâm là điểm \(I\). Gọi \(G\left( {1; - 2} \right)\) và \(K\left( {3;1} \right)\) lần lượt là trọng tâm các tam giác \(ACD\) và $ABI$. Biết $A\left( {a;b} \right)$ với \(b > 0\). Khi đó \({a^2} + {b^2}\) bằng
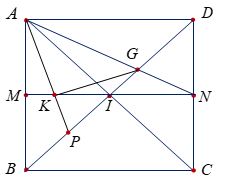
Gọi $M$, $N$ và $P$ lần lượt là các trung điểm của $AB$, $CD$ và $BI$. Ta có
\(\overrightarrow {AK} = \dfrac{2}{3}\overrightarrow {AP} \)\( = \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AI} } \right)\)\( = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{6}\overrightarrow {AD} \)
\(\overrightarrow {AG} = \dfrac{2}{3}\overrightarrow {AN} \)\( = \dfrac{1}{3}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right)\)\( = \dfrac{2}{3}\overrightarrow {AD} + \dfrac{1}{3}\overrightarrow {AB} \)
\(\overrightarrow {KG} = \overrightarrow {AG} - \overrightarrow {AK} \)\( = \dfrac{1}{2}\overrightarrow {AD} - \dfrac{1}{6}\overrightarrow {AB} \).
Suy ra: \(\overrightarrow {AK} .\overrightarrow {KG} = \dfrac{1}{{12}}A{D^2} - \dfrac{1}{{12}}A{B^2} = 0\) vì \(AB = AD\) và \(\overrightarrow {AB} .\overrightarrow {AD} = 0\)
Đồng thời
\(A{K^2} = \dfrac{5}{{18}}A{B^2}\)\( = K{G^2} = \dfrac{5}{{18}}A{B^2}\). Do đó tam giác \(AKG\) vuông cân tại \(K\) nên:
\(\left\{ \begin{array}{l}\overrightarrow {AK} .\overrightarrow {KG} = 0\\A{K^2} = G{K^2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + 3b = 9\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = 13\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{9 - 2a}}{3}\\13{a^2} - 78a = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = \dfrac{{9 - 2a}}{3}\\\left[ \begin{array}{l}a = 0\\a = 6\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 0\\b = 3\left( {tm} \right)\end{array} \right.\\\left\{ \begin{array}{l}a = 6\\b = - 1\left( {loai} \right)\end{array} \right.\end{array} \right.\) \( \Rightarrow {a^2} + {b^2} = 9\).
Trong mặt phẳng tọa độ $Oxy$, cho ba điểm \(A\left( {1;0} \right)\), \(B\left( {0;5} \right)\) và \(C\left( { - 3; - 5} \right)\). Tìm tọa độ điểm \(M\) thuộc trục \(Oy\) sao cho \(\left| {3\overrightarrow {MA} - 2\overrightarrow {MB} + 4\overrightarrow {MC} } \right|\) đạt giá trị nhỏ nhất?
Gọi \(I\left( {a;b} \right)\) là điểm thỏa mãn: \(3\overrightarrow {IA} - 2\overrightarrow {IB} + 4\overrightarrow {IC} = \overrightarrow 0 \)
ta có: \(3\overrightarrow {IA} - 2\overrightarrow {IB} + 4\overrightarrow {IC} = \overrightarrow 0 \) \( \Leftrightarrow 5\overrightarrow {IA} = 2\overrightarrow {AB} - 4\overrightarrow {AC} \) \( \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{9}{5}\\b = - 6\end{array} \right.\) \( \Rightarrow I\left( { - \dfrac{9}{5}; - 6} \right)\)
Khi đó \(\left| {3\overrightarrow {MA} - 2\overrightarrow {MB} + 4\overrightarrow {MC} } \right|\) \( = \left| {3\overrightarrow {IA} - 2\overrightarrow {IB} + 4\overrightarrow {IC} - 5\overrightarrow {IM} } \right|\) \( = \left| {\overrightarrow 0 - 5\overrightarrow {IM} } \right|\) \( = 5IM\)
Do đó: \(\left| {3\overrightarrow {MA} - 2\overrightarrow {MB} + 4\overrightarrow {MC} } \right|\) nhỏ nhất khi \(IM\) ngắn nhất. Suy ra \(M\) là hình chiếu vuông góc của \(I\left( { - \dfrac{9}{5}; - 6} \right)\) trên \(Oy\) \( \Rightarrow M\left( {0; - 6} \right)\).
Trong mặt phẳng với hệ tọa độ \(Oxy\) cho đường thẳng \(\Delta :\,x - 2y - 5 = 0\) và các điểm \(A\left( {1;\,2} \right)\), \(B\left( { - 2;\,3} \right)\), \(C\left( { - 2;\,1} \right)\). Viết phương trình đường thẳng \(d\), biết đường thẳng \(d\) đi qua gốc tọa độ và cắt đường thẳng \(\Delta \) tại điểm \(M\) sao cho: \(\left| {\overrightarrow {MA\,} + \overrightarrow {MB\,} + \overrightarrow {MC\,} } \right|\) nhỏ nhất.
Gọi \(M\left( {2m + 5;m} \right) \in \Delta \).
\(G\left( { - 1;2} \right)\) là trọng tâm \(\Delta ABC\).
$\left| {\overrightarrow {MA\,} + \overrightarrow {MB\,} + \overrightarrow {MC\,} } \right| = \left| {3\overrightarrow {MG} } \right| = 3MG$.
\(\left| {\overrightarrow {MA\,} + \overrightarrow {MB\,} + \overrightarrow {MC\,} } \right|\) nhỏ nhất \( \Leftrightarrow MG\) nhỏ nhất \( \Leftrightarrow G\) là hình chiếu vuông góc của \(G\) trên \(\Delta \).
\(\overrightarrow {GM} = \left( {2m + 6;m - 2} \right)\); VTCP của \(\Delta \) là \(\overrightarrow u = \left( {2;1} \right)\).
\(G\) là hình chiếu vuông góc của \(G\) trên \(\Delta \) \( \Leftrightarrow \overrightarrow {GM} .\overrightarrow u = 0 \Leftrightarrow 2\left( {2m + 6} \right) + m - 2 = 0 \Leftrightarrow 5m + 10 = 0 \Leftrightarrow m = - 2 \Rightarrow M\left( {1; - 2} \right)\).
Đường thẳng \(d\) qua gốc tọa độ \(d:y = ax\).
\(M\left( {1; - 2} \right) \in d \Rightarrow a = - 2\).
Vậy phương trình đường thẳng \(d:2x + y = 0\)
Trong mặt phẳng với hệ tọa độ \(Oxy\) cho hình chữ nhật \(ABCD\) biết \(AD = 2AB\), đường thẳng \(AC\) có phương trình \(x + 2y + 2 = 0\), \(D\left( {1;\,1} \right)\) và \(A\left( {a;\,b} \right)\,\,\,\,\,\,\left( {a,\,b \in \mathbb{R},\,a > 0} \right)\). Tính \(a + b\).
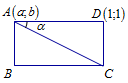
Cách 1: Gọi \(A\left( {a;b} \right)\). Vì \(A \in AC:x + 2y + 2 = 0\) nên \(a + 2b + 2 = 0 \Rightarrow a = - 2b - 2\)
Do \(a > 0\) nên \( - 2b - 2 > 0 \Rightarrow b < - 1\) \(\,\left( * \right)\)
Khi đó \(A\left( { - 2b - 2;b} \right)\).
Ta có \(\overrightarrow {AD} = \left( {2b + 3;1 - b} \right)\) là véctơ chỉ phương của đường thẳng \(AD\).
\(\vec u = \left( {2; - 1} \right)\) là véctơ chỉ phương của đường thẳng \(AC\).
Trên hình vẽ, \(\tan \alpha = \dfrac{{DC}}{{AD}} = \dfrac{1}{2} \Rightarrow \cos \alpha = \dfrac{2}{{\sqrt 5 }}\) \(\left( 1 \right)\)
Lại có \(\cos \alpha = \dfrac{{\left| {\overrightarrow {AD} .\vec u} \right|}}{{\left| {\overrightarrow {AD} } \right|.\left| {.\vec u} \right|}} = \dfrac{{5\left| {b + 1} \right|}}{{\sqrt 5 \sqrt {{b^2} + 2b + 2} }}\) \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\dfrac{{5\left| {b + 1} \right|}}{{\sqrt 5 \sqrt {{b^2} + 2b + 2} }} = \dfrac{2}{{\sqrt 5 }} \Leftrightarrow {b^2} + 2b - 3 = 0 \Rightarrow b = - 3\) (do \(\left( * \right)\)) \( \Rightarrow a = 4\).
Khi đó \(A\left( {4; - 3} \right)\), suy ra \(a + b = 1\).
Cách 2: Gọi \(A\left( {a;b} \right)\). Vì \(A \in AC:x + 2y + 2 = 0\) nên \(a + 2b + 2 = 0 \Rightarrow a = - 2b - 2\)
Do \(a > 0\) nên \( - 2b - 2 > 0 \Rightarrow b < - 1\)\(\,\left( * \right)\), khi đó \(A\left( { - 2b - 2;b} \right)\).
Vì \(C \in AC:x + 2y + 2 = 0\) nên \(C\left( { - 2c - 2;c} \right)\)
Ta có: \(\overrightarrow {AD} = \left( {3 + 2b; - 1 - b} \right)\); \(\overrightarrow {CD} = \left( {3 + 2c;1 - c} \right)\).
Chọn \(\left\{ \begin{array}{l}\vec u \bot \overrightarrow {CD} \\\left| {\vec u} \right| = \left| {\overrightarrow {CD} } \right|\end{array} \right. \Rightarrow \vec u = \left( {c - 1;3 + 2c} \right)\)
Ta có: \(\left\{ \begin{array}{l}AD \bot CD\\AB = 2CD\end{array} \right. \Rightarrow \left[ \begin{array}{l}\overrightarrow {AD} = 2\vec u\\\overrightarrow {AD} = - 2\vec u\end{array} \right.\)
* Với \(\overrightarrow {AD} = 2\vec u\) \( \Rightarrow \left\{ \begin{array}{l}3 + 2b = 2c - 2\\1 - b = 6 + 4c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 3\\c = - \dfrac{1}{2}\end{array} \right.\) (t/m)
* Với \(\overrightarrow {AD} = - 2\vec u\) \( \Rightarrow \left\{ \begin{array}{l}3 + 2b = - 2c + 2\\1 - b = - 6 - 4c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 1\\c = - \dfrac{3}{2}\end{array} \right.\) (không t/m)
Vậy \(A\left( {4; - 3} \right)\), suy ra \(a + b = 1\).
Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) có \(A\left( { - 4; - 1} \right)\), hai đường cao \(BH\) và \(CK\) có phương trình lần lượt là \(2x - y + 3 = 0\) và \(3x + 2y - 6 = 0\). Viết phương trình đường thẳng \(BC\) và tính diện tích tam giác \(ABC\).
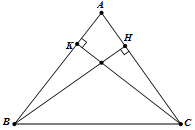
+ \(BH\) có véctơ pháp tuyến ${\overrightarrow n _{_{BH}}}\left( {2; - 1} \right)$. \(CK\) có véctơ pháp tuyến ${\overrightarrow n _{_{CK}}}\left( {3;2} \right)$.
+ Đường thẳng \(AB\) vuông góc \(CK\) nên nhận ${\overrightarrow n _{_{CK}}}\left( {3;2} \right)$ làm véctơ chỉ phương, vì thế \(AB\) có véctơ pháp tuyến ${\overrightarrow n _{_{AB}}}\left( {2; - 3} \right)$. Mặt khác \(AB\) đi qua \(A\left( { - 4; - 1} \right)\) nên có phương trình:
\(2\left( {x + 4} \right) - 3\left( {y + 1} \right) = 0\) \( \Leftrightarrow 2x - 3y + 5 = 0\).
+ Đường thẳng \(AC\) vuông góc \(BH\) nên nhận ${\overrightarrow n _{_{BH}}}\left( {2; - 1} \right)$ làm véctơ chỉ phương, vì thế \(AC\) có véctơ pháp tuyến ${\overrightarrow n _{_{AC}}}\left( {1;2} \right)$. Mặt khác \(AC\) đi qua \(A\left( { - 4; - 1} \right)\) nên có phương trình:
\(1\left( {x + 4} \right) + 2\left( {y + 1} \right) = 0\) \( \Leftrightarrow x + 2y + 6 = 0\).
+ \(B\) là giao điểm của \(AB\) và \(BH\). Xét hệ: \(\left\{ \begin{array}{l}2x - 3y + 5 = 0\\2x - y + 3 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = 1\end{array} \right.\) \( \Rightarrow B\left( { - 1;1} \right)\).
+ \(C\) là giao điểm của \(AC\) và \(CK\). Xét hệ: \(\left\{ \begin{array}{l}x + 2y + 6 = 0\\3x + 2y - 6 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y = - 6\end{array} \right.\) \( \Rightarrow C\left( {6; - 6} \right)\).
+ Đường thẳng \(BC\) có véctơ chỉ phương là \(\overrightarrow {BC} = \left( {7; - 7} \right)\) nên có véctơ pháp tuyến là \(\overrightarrow n = \left( {7;7} \right)\). Vậy \(BC\) có phương trình: \(7\left( {x + 1} \right) + 7\left( {y - 1} \right) = 0\) \( \Leftrightarrow x + y = 0\).
+ \(BC = \sqrt {{7^2} + {{\left( { - 7} \right)}^2}} = 7\sqrt 2 \).
+ Chiều cao kẻ từ \(A\) của tam giác \(ABC\) là \(d\left( {A,BC} \right) = \dfrac{{\left| { - 4 - 1} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \dfrac{5}{{\sqrt 2 }}\).
+ Diện tích tam giác \(ABC\) là: \(S = \dfrac{1}{2}.7\sqrt 2 .\dfrac{5}{{\sqrt 2 }}\)\( = \dfrac{{35}}{2}\).
Cho\(A\left( {1;\, - 1} \right)\), \(B\left( {3;\,2} \right)\). Tìm \(M\) trên trục $Oy$ sao cho $M{A^2} + M{B^2}$ nhỏ nhất.
\(M\) trên trục $Oy$ \( \Rightarrow M\left( {0;\,y} \right)\).
$\overrightarrow {MA} = \left( {1;\, - 1 - y} \right);$ $\overrightarrow {MB} = \left( {3;2 - y} \right)$
$M{A^2} + M{B^2} = 10 - 2y + 2{y^2} = 2\left( {{y^2} - y + \dfrac{1}{4}} \right) + \dfrac{{19}}{2}$ $ = 2{\left( {y - \dfrac{1}{2}} \right)^2} + \dfrac{{19}}{2}$ \( \ge \dfrac{{19}}{2}\)
Giá trị nhỏ nhất của \(\left( {M{A^2} + M{B^2}} \right)\) bằng \(\dfrac{{19}}{2}\)
Dấu bằng xảy ra khi \(y = \dfrac{1}{2}\).
Cho tam giác $ABC$ có $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và hai trong ba đường phân giác trong có phương trình lần lượt là $x - 2y - 1 = 0$, $x + 3y - 1 = 0$. Viết phương trình đường thẳng chứa cạnh $BC$.
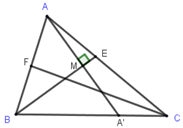
Dễ thấy điểm $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ không thuộc hai đường phân giác $x - 2y - 1 = 0$ và $x + 3y - 1 = 0$.
Gọi $CF: x - 2y - 1 = 0$, $BE: x + 3y - 1 = 0$ lần lượt là phương trình đường phân giác xuất phát từ đỉnh $C$, $B$ (như hình vẽ trên).
Gọi $d$ là đường thẳng qua $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và vuông góc với $BE$ thì $d$ có VTPT là $\overrightarrow {{n_d}} = \left( {3; - 1} \right)$ nên có phương trình $3\left( {x - \dfrac{4}{5}} \right) - \left( {y - \dfrac{7}{5}} \right) = 0 \Leftrightarrow $ $3x - y - 1 = 0$.
Tọa độ điểm $M = d \cap BE$ thỏa mãn hệ $\left\{ \begin{array}{l}3x - y - 1 = 0\\x + 3y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{5}\\y = \dfrac{1}{5}\end{array} \right. \Rightarrow $ $M\left( {\dfrac{2}{5};\dfrac{1}{5}} \right)$.
Suy ra tọa độ điểm đối xứng với $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ qua $M\left( {\dfrac{2}{5};\dfrac{1}{5}} \right)$ là $A'\left( {0; - 1} \right)$ thì $A' \in BC$ $\left( 1 \right)$.
Gọi $d'$ là đường thẳng qua $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và vuông góc với $CF$ thì $d'$ có VTPT là $\overrightarrow {{n_{d'}}} = \left( {2;1} \right)$ nên có phương trình $2\left( {x - \dfrac{4}{5}} \right) + \left( {y - \dfrac{7}{5}} \right) = 0 \Leftrightarrow $ $2x + y - 3 = 0$.
Tọa độ điểm $N = d' \cap CF$ thỏa mãn hệ $\left\{ \begin{array}{l}2x + y - 3 = 0\\x - 2y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{5}\\y = \dfrac{1}{5}\end{array} \right. \Rightarrow $ $N\left( {\dfrac{7}{5};\dfrac{1}{5}} \right)$.
Suy ra tọa độ điểm đối xứng với $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ qua $N\left( {\dfrac{7}{5};\dfrac{1}{5}} \right)$ là $A''\left( {2; - 1} \right)$ thì $A'' \in BC$ $\left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có $\overrightarrow {A'A''} = \left( {2;0} \right)$ là một VTCP của $BC$ suy ra VTPT của $BC$ là $\overrightarrow n = \left( {0;1} \right)$. Do đó phương trình cạnh $BC: 0\left( {x - 0} \right) + 1\left( {y + 1} \right) = 0 \Leftrightarrow $ $y + 1 = 0$.
Cho đường tròn \(\left( C \right):\,{x^2} + {y^2} - 2x + 2y - 7 = 0\) và đường thẳng \(d:\,x + y + 1 = 0\). Tìm tất cả các đường thẳng song song với đường thẳng \(d\) và cắt đường tròn \(\left( C \right)\) theo dây cung có độ dài bằng \(2\).
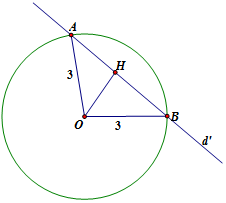
Tâm \(O\left( {1;\, - 1} \right)\), bán kính \(R = \sqrt {{1^2} + {{\left( { - 1} \right)}^2} - \left( { - 7} \right)} = 3\)
Gọi đường thẳng cần tìm là \(\left( {d'} \right):x + y + c = 0\).
Gọi \(A,\,B\) lần lượt là giao điểm của \(\left( {d'} \right)\) và \(\left( C \right)\).
Xét \(\Delta OHB\) vuông tại \(H\) (\(H\) là chân đường cao kẻ từ \(O\) trong tam giác \(OAB\)).
Ta có: \(d\left( {O,\,AB} \right) = \dfrac{{\left| {1 + \left( { - 1} \right) + c} \right|}}{{\sqrt 2 }}\) \( = OH\) \( = \sqrt {O{B^2} - B{H^2}} \) \( = \sqrt {{3^2} - {1^2}} = 2\sqrt 2 \).
\( \Leftrightarrow \dfrac{{\left| c \right|}}{{\sqrt 2 }} = 2\sqrt 2 \) \( \Leftrightarrow \left| c \right| = 4 \Leftrightarrow c = \pm 4\).
Vậy đường thẳng cần tìm có dạng \(x + y + 4 = 0\) hoặc \(x + y - 4 = 0\).
Đường thẳng nào dưới đây tiếp xúc với đường tròn \({\left( {x - 2} \right)^2} + {{y}^2} = 4\), tại $M$ có hoành độ ${x_M} = 3$?
Thế ${x_M} = 3$ vào phương trình đường tròn, ta được: ${y^2} = 3 \Leftrightarrow \left[ \begin{array}{l}y = \sqrt 3 \\y = - \sqrt 3 \end{array} \right.$
$ \Rightarrow {M_1}\left( {3;\sqrt 3 } \right)$, ${M_2}\left( {3; - \sqrt 3 } \right)$.
Đường tròn $\left( C \right)$ có tâm $I\left( {2;0} \right)$.
- Với $I\left( {2;0} \right)$, ${M_1}\left( {3;\sqrt 3 } \right)$ ta có $\overrightarrow {I{M_1}} = \left( {1;\sqrt 3 } \right)$.
Đường thẳng qua ${M_1}\left( {3;\sqrt 3 } \right)$ và nhận $\overrightarrow {I{M_1}} = \left( {1;\sqrt 3 } \right)$ làm véctơ pháp tuyến có phương trình là $\left( {x - 3} \right) + \sqrt 3 \left( {y - \sqrt 3 } \right) = 0$ $ \Leftrightarrow x + \sqrt 3 y - 6 = 0$.
- Với $I\left( {2;0} \right)$, ${M_2}\left( {3; - \sqrt 3 } \right)$ ta có $\overrightarrow {I{M_2}} = \left( {1; - \sqrt 3 } \right)$.
Đường thẳng qua ${M_2}\left( {3; - \sqrt 3 } \right)$ và nhận $\overrightarrow {I{M_2}} = \left( {1; - \sqrt 3 } \right)$ làm véctơ pháp tuyến có phương trình là $\left( {x - 3} \right) - \sqrt 3 \left( {y + \sqrt 3 } \right) = 0$ $ \Leftrightarrow x - \sqrt 3 y - 6 = 0$.
Vậy đường thẳng tiếp xúc với đường tròn \({\left( {x - 2} \right)^2} + {{y}^2} = 4\) tại $M$ có hoành độ ${x_M} = 3$ là $x + \sqrt 3 y - 6 = 0$ hoặc $x - \sqrt 3 y - 6 = 0$.
Đường tròn đi qua \(A\left( {2;\,4} \right)\), tiếp xúc với các trục tọa độ có phương trình là
Đường tròn \(\left( C \right)\) có tâm \(I\left( {a;\,b} \right)\), bán kính \(R\) có phương trình là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)
Ta có đường tròn \(\left( C \right)\) đi qua \(A\left( {2;\,4} \right)\) nên ta có: \({\left( {2 - a} \right)^2} + {\left( {4 - b} \right)^2} = {R^2}\) \(\left( 1 \right)\)
Đường tròn \(\left( C \right)\)tiếp xúc với các trục tọa độ, ta phải có \(\left| a \right| = \left| b \right| = R\) \(\left( 2 \right)\)
- Trường hợp 1: Nếu \(a = b\), thay vào \(\left( 1 \right)\) ta có
\({\left( {2 - a} \right)^2} + {\left( {4 - a} \right)^2} = {a^2} \Leftrightarrow {a^2} - 12a + 20 = 0 \Leftrightarrow \left[ \begin{array}{l}a = 2\\a = 10\end{array} \right.\)
Với \(a = 2\) ta có phương trình đường tròn \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\)
Với \(a = 10\) ta có phương trình đường tròn \({\left( {x - 10} \right)^2} + {\left( {y - 10} \right)^2} = 100\)
- Trường hợp 2: Nếu \(a = - b\), thay vào \(\left( 1 \right)\) ta có phương trình
\({\left( {2 - a} \right)^2} + {\left( {4 + a} \right)^2} = {a^2} \Leftrightarrow {a^2} + 4a + 20 = 0\): phương trình này vô nghiệm.
Vậy các đường tròn có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\), \({\left( {x - 10} \right)^2} + {\left( {y - 10} \right)^2} = 100\) thỏa mãn yêu cầu bài toán.
Cho đường tròn \(\left( C \right):{x^2} + {y^2} + 6x - 2y + 5 = 0\) và điểm \(A\left( { - 4;2} \right)\). Đường thẳng \(d\) qua \(A\) cắt \(\left( C \right)\) tại \(2\) điểm \(M\), \(N\) sao cho \(A\) là trung điểm của \(MN\) có phương trình là
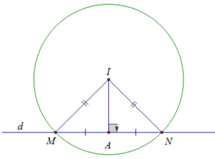
\(\left( C \right)\) có tâm \(I\left( { - 3;1} \right)\), bán kính \(R = \sqrt 5 \).
Đường thẳng qua \(A\left( { - 4;2} \right)\) có véc tơ pháp tuyến \(\overrightarrow {\,n\,} = \left( {a;b} \right)\) \(\left( {{a^2} + {b^2} \ne 0} \right)\) có phương trình dạng \(d:ax + by + 4a - 2b = 0\).
Tam giác \(IMN\) cân tại \(I\) có \(A\) là trung điểm \(MN\) nên $IA \bot MN$.
\( \Rightarrow d\left( {I;d} \right) = IA \Leftrightarrow \dfrac{{\left| {a - b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \sqrt 2 \Leftrightarrow {\left( {a - b} \right)^2} = 2\left( {{a^2} + {b^2}} \right) \Leftrightarrow a = - b\).
Chọn \(a = 1 \Rightarrow b = - 1\). Vậy phương trình đường thẳng \(d:x - y + 6 = 0\).
Một miếng giấy hình tam giác $ABC$ vuông tại \(A\) có diện tích $S$, gọi $I$ là trung điểm $BC$ và $O$ là trung điểm của $AI$. Cắt miếng giấy theo một đường thẳng qua $O$, đường thẳng này đi qua $M$, $N$ lần lượt trên các cạnh $AB$, $AC$. Khi đó diện tích miếng giấy chứa điểm$A$ có diện tích thuộc đoạn:
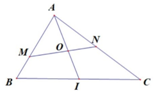
Đặt \(A\left( {0;\,0} \right)\), \(B\left( {4b;\,0} \right)\), \(C\left( {0;\,4c} \right)\) \( \Rightarrow \)\(I\left( {2b;2c} \right)\), \(O\left( {b,\,c} \right)\).
Đặt \(M\left( {t,\,0} \right)\) \( \Rightarrow \) \(N\left( {0,\,\dfrac{{ - ct}}{{b - t}}} \right)\).
Khi đó: \({S_{\Delta ABC}} = 8bc\), \({S_{\Delta AMN}} = \dfrac{{c{t^2}}}{{2\left( {t - b} \right)}} = \dfrac{c}{2}.f\left( t \right)\) với \(\dfrac{{4b}}{3} \le t \le 4b\).
Xét \(f\left( t \right) = \dfrac{{{t^2}}}{{t - b}}\) trong \(\left[ {\dfrac{{4b}}{3};4b} \right]\) ta có:
\(f\left( t \right) = \dfrac{{{t^2}}}{{t - b}}\)\( = t + b + \dfrac{{{b^2}}}{{t - b}}\)\( = t - b + \dfrac{{{b^2}}}{{t - b}} + 2b\) \( \ge 2\sqrt {\left( {t - b} \right).\dfrac{{{b^2}}}{{t - b}}} + 2b\) \( = 2b + 2b = 4b\)
Do đó \(f\left( t \right) \ge 4b,\forall t \in \left[ {\dfrac{{4b}}{3};4b} \right]\).
Dấu \('' = ''\) xảy ra khi \(t - b = \dfrac{{{b^2}}}{{t - b}} \Leftrightarrow t = 2b\).
Vậy \(\mathop {\min }\limits_{\left[ {\dfrac{{4b}}{3};4b} \right]} f\left( t \right) = 4b\) hay \(\min {S_{AMN}} = \dfrac{c}{2}.4b = 2bc\) khi \(t = 2b\).
\({f_{\max }} = \dfrac{{8bc}}{3}\) khi \(t = \dfrac{{4b}}{3} \vee t = 4b\)
\( \Rightarrow \)\(\dfrac{{{S_{ABC}}}}{4} \le {S_{AMN}} \le \dfrac{{{S_{ABC}}}}{3}\).
Cho \(\left( E \right)\) có hai tiêu điểm \({F_1}\left( { - \sqrt 7 ;0} \right)\), \({F_2}\left( {\sqrt 7 ;0} \right)\) và điểm \(M\left( { - \sqrt 7 ;\dfrac{9}{4}} \right)\) thuộc \(\left( E \right)\). Gọi \(N\) là điểm đối xứng với \(M\) qua gốc tọa độ \(O.\) Khi đó
\(N\) đối xứng với \(M\) qua gốc tọa độ \(O\) nên \(N\left( {\sqrt 7 ; - \dfrac{9}{4}} \right)\).
Ta có: \(M{F_1} = \dfrac{9}{4}; M{F_2} = \dfrac{{23}}{4}; N{F_1} = \dfrac{{23}}{4}; N{F_2} = \dfrac{9}{4}\).
Do đó \(N{F_2} + M{F_1} = \dfrac{9}{2}.\)

