Các định nghĩa về véc tơ

Véc tơ là một đoạn thẳng có hướng.

Hai vectơ cùng phương thì hoặc cùng hướng hoặc ngược hướng nên hai véc tơ ngược hướng chắc chắn cùng phương.

Hai véc tơ được gọi là bằng nhau nếu chúng cùng hướng và cùng độ dài.

Ba điểm \(A,B,C\) thẳng hàng nếu và chỉ nếu véc tơ \(\overrightarrow {AB} \) cùng phương véc tơ \(\overrightarrow {AC} \).

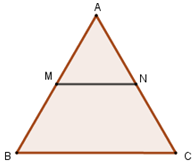
Quan sát hình vẽ ta thấy hai véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {MB} \) là cùng hướng.

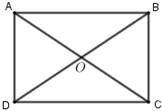
Hai véc tơ \(\overrightarrow {OA} \) và \(\overrightarrow {OC} \) đối nhau nên A sai.

Hai véc tơ \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \) ngược hướng nên B sai.

Hai véc tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \) không cùng phương nên C sai.

\(\left| {\overrightarrow {AC} } \right| = \left| {\overrightarrow {BD} } \right|\) đúng vì đều là độ dài đường chéo hình chữ nhật.

Ta có : \(\left| {\overrightarrow {AA} } \right| = \left| {\overrightarrow 0 } \right| = 0\) nên A sai.

\(\overrightarrow {BB}  = \overrightarrow 0 \) nên B sai.

\(\left| {\overrightarrow {AB} } \right| = AB > 0\) vì hai điểm \(A,B\) phân biệt hay \(C\) đúng.

\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BA} } \right| = AB\) nên D sai.

Tam giác đều \(ABC \Rightarrow \overrightarrow {AB} ,\overrightarrow {BC} \) không cùng hướng \( \Rightarrow \overrightarrow {AB}  \ne \overrightarrow {BC} \) nên A sai.

Hai véc tơ \(\overrightarrow {AC} \) và \(\overrightarrow {BC} \) không cùng phương nên chúng không cùng hướng và không bằng nhau. B và D sai.

\(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {BC} } \right|\) đúng vì đều là độ dài cạnh của tam giác đều. C đúng.

Ta có các vectơ đó là: \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {CB} \).

Xét các vectơ có điểm \(A\) là điểm đầu thì có các vectơ thỏa mãn bài toán là \(\overrightarrow {AB}, \overrightarrow {AC}, \overrightarrow {AD} \) \( \Rightarrow \) có 3 vectơ.

Tương tự cho các điểm còn lại \(B,C,D.\)

Ta có \(C\) là trung điểm của đoạn \(AB\) nên \(\overrightarrow {AC}  = \overrightarrow {CB} \).

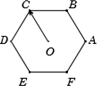
Có \(6\) véc tơ thỏa mãn bài toán, đó là các vectơ: \(\overrightarrow {AB} ,\;\overrightarrow {BA} ,\;\overrightarrow {DE} ,\;\overrightarrow {ED} ,\;\overrightarrow {FC} ,\;\overrightarrow {CF} \).

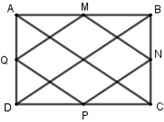
Ta thấy, \(MN//QP//AC\) và \(MN = QP = \dfrac{1}{2}AC\). Hơn nữa \(\overrightarrow {MN} \) và \(\overrightarrow {QP} \) cùng hướng nên \(\overrightarrow {MN}  = \overrightarrow {QP} \) nên A đúng.

\(\left| {\overrightarrow {QP} } \right| = \left| {\overrightarrow {MN} } \right| = \dfrac{1}{2}AC\) nên B đúng.

\(MQ//NP//BD\) và \(MQ = NP = \dfrac{1}{2}BD\). Hơn nữa \(\overrightarrow {MQ} \) và \(\overrightarrow {NP} \) cùng hướng nên \(\overrightarrow {MQ}  = \overrightarrow {NP} \) nên C đúng.

\(\left| {\overrightarrow {MN} } \right| = MN = \dfrac{1}{2}AC\) nên D sai.

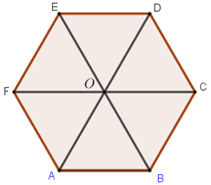
Đáp án A: \(\overrightarrow {AB}  = \overrightarrow {ED} \) đúng.

Đáp án B: \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AF} } \right|\) đúng vì đều là cạnh của lục giác đều.

Đáp án C: \(\overrightarrow {OD}  = \overrightarrow {BC} \) đúng vì cùng hướng và cùng độ dài.

Đáp án D: \(\overrightarrow {OB}  = \overrightarrow {OE} \) sai vì hai véctơ ngược hướng.

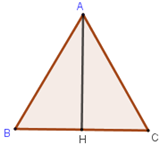
Tam giác \(ABC\) đều cạnh \(a\), trung điểm \(H\) của \(BC\) nên \(AC = AB = BC = a\) và \(BH = HC = \dfrac{a}{2}\).

Tam giác \(ABH\) vuông tại \(H\) nên \(A{H^2} + B{H^2} = A{B^2}\) \( \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} \)\( = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\).

Do đó \(\left| {\overrightarrow {HB} } \right| = HB = \dfrac{a}{2}\) nên A đúng.

\(\left| {\overrightarrow {AH} } \right| = AH = \dfrac{{a\sqrt 3 }}{2}\) nên B đúng.

\(\left| {\overrightarrow {CH} } \right| = CH = \dfrac{a}{2}\) nên C sai.

\(\left| {\overrightarrow {BH} } \right| = \left| {\overrightarrow {HC} } \right| = \dfrac{a}{2}\) nên D đúng.

Tam giác \(ABD\) có \(AB = AD = a\) và \(\widehat {BAD} = 60^\circ \) nên là tam giác đều cạnh \(a\).

Do đó \(BD = AB = AD = a\) \( \Rightarrow \left| {\overrightarrow {BD} } \right| = BD = a\).

Ngoài ra các đáp án A, C sai vì mỗi cặp véc tơ đều không cùng phương.

Đáp án D sai vì \(\overrightarrow {BC}  = \overrightarrow {AD} \) chứ không phải \(\overrightarrow {BC}  = \overrightarrow {DA} \).

Ta có \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {CD} } \right| \Leftrightarrow AB = CD\). Suy ra tập hợp các điểm \(D\) thỏa mãn yêu cầu bài toán là đường tròn tâm \(C,\) bán kính \(AB\).

Véc tơ là một đoạn thẳng có hướng.

Định nghĩa hai véc tơ đối nhau:

Hai vecto đối nhau nếu chúng ngược hướng và cùng độ dài.

Hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài.