Dấu của nhị thức bậc nhất

TH1: $x \ge \dfrac{4}{3}$

$\left| {2x + 3} \right| - \left| {3x - 4} \right| \ge  - 5$

$\begin{array}{l} \Leftrightarrow 2x + 3 - 3x + 4 \ge  - 5\\ \Leftrightarrow x \le 12\end{array}$

$\Rightarrow \dfrac{4}{3} \le x \le 12$

TH2: $- \dfrac{3}{2} \le x \le \dfrac{4}{3}$

$\left| {2x + 3} \right| - \left| {3x - 4} \right| \ge  - 5$

$\begin{array}{l} \Leftrightarrow 2x + 3 + 3x - 4 \ge  - 5\\ \Leftrightarrow x \ge  - \dfrac{4}{5}\end{array}$

$\Rightarrow  - \dfrac{4}{5} \le x \le \dfrac{4}{3}$

TH3: $x \le  - \dfrac{3}{2}$

$\left| {2x + 3} \right| - \left| {3x - 4} \right| \ge  - 5$

$\begin{array}{l} \Leftrightarrow  - 2x - 3 + 3x - 4 \ge  - 5\\ \Leftrightarrow x \ge 2\end{array}$ (Loại)

 $\Rightarrow x \in \left[ { - \dfrac{4}{5};12} \right] \Rightarrow$Đoạn có độ dài bằng $\dfrac{{64}}{5}$.

Nhị thức $f\left( x \right) = 3x + 2$ nhận giá trị âm khi $x <  - \dfrac{2}{3}$  

Ta có với $x \in \left( { - \dfrac{b}{a}; + \infty } \right)$ thì hàm số cùng dấu với hệ số $a > 0$

Vậy D đúng.

ĐKXĐ: $x \ne 0$

$\dfrac{2}{x} >  - 1 \Leftrightarrow \dfrac{2}{x} + 1 > 0 \Leftrightarrow \dfrac{{2 + x}}{x} > 0 \Leftrightarrow \left[ \begin{array}{l}x <  - 2\\x > 0\end{array} \right.$ 

Kết hợp với ĐKXĐ ta được tập nghiệm của BPT là $\left( { - \infty ; - 2} \right) \cup \left( {0; + \infty } \right).$

Ta có $x = 0;\,\,x - 2 = 0 \Leftrightarrow x = 2$ và $3 - x = 0 \Leftrightarrow x = 3.$Bảng xét dấu

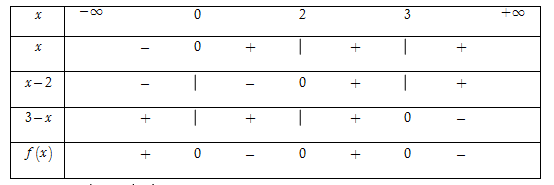
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow x \in \left( {0;2} \right) \cup \left( {3; + \,\infty } \right).$

Ta có $f\left( x \right) = 0 \Leftrightarrow 9{x^2} - 1 = 0 \Leftrightarrow \left( {3x - 1} \right)\left( {3x + 1} \right) = 0.$

Phương trình $3x - 1 = 0 \Leftrightarrow x = \dfrac{1}{3}$ và $3x + 1 = 0 \Leftrightarrow x =  - \dfrac{1}{3}.$

Bảng xét dấu

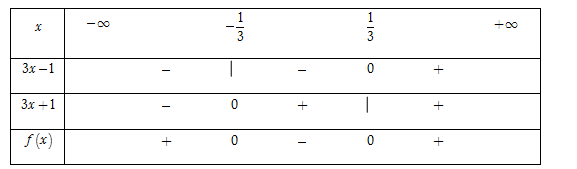
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \dfrac{1}{3};\dfrac{1}{3}} \right).$

Ta có $\left( {2x - 1} \right)\left( {{x^3} - 1} \right) = 0 \Leftrightarrow \left( {2x - 1} \right)\left( {x - 1} \right)\left( {{x^2} + x + 1} \right) = 0.$

Phương trình $2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2};\,\,x - 1 = 0 \Leftrightarrow x = 1$ và ${x^2} + x + 1 = {\left( {x + \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} > 0.$

Bảng xét dấu

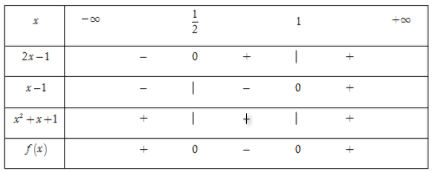
Dựa vào bảng xét dấu, suy ra $f\left( x \right) \ge 0 \Leftrightarrow x \in \left( { - \,\infty ;\dfrac{1}{2}} \right] \cup \left[ {1; + \,\infty } \right).$

Ta có $f\left( x \right) \ge 0 \Leftrightarrow 2x - 4 \ge 0 \Leftrightarrow x \ge 2 \Leftrightarrow x \in \left[ {2; + \,\infty } \right).$

$\sqrt {x + 2}  < 2x + 1 \Leftrightarrow \left\{ \begin{array}{l}x + 2 \ge 0\\2x + 1 > 0\\x + 2 < 4{x^2} + 4x + 1\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x \ge  - 2\\x >  - \dfrac{1}{2}\\4{x^2} + 3x - 1 > 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}x >  - \dfrac{1}{2}\\\left[ \begin{array}{l}x <  - 1\\x > \dfrac{1}{4}\end{array} \right.\end{array} \right.$$\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x >  - \dfrac{1}{2}\\x <  - 1\end{array} \right.\left( {VN} \right)\\\left\{ \begin{array}{l}x >  - \dfrac{1}{2}\\x > \dfrac{1}{4}\end{array} \right. \Leftrightarrow x > \dfrac{1}{4}\end{array} \right.$

Vậy BPT có tập nghiệm là $\left( {\dfrac{1}{4}; + \infty } \right).$ 

Phương trình $4x - 8 = 0 \Leftrightarrow x = 2;\,\,2 + x = 0 \Leftrightarrow x =  - \,2$ và $4 - x = 0 \Leftrightarrow x = 4.$

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \ge 0 \Leftrightarrow x \in x \in \left( { - \,\infty ; - 2} \right] \cup \left[ {2;4} \right).$

Phương trình $x = 0;\,\,x - 3 = 0 \Leftrightarrow x = 3;\,\,x - 5 = 0 \Leftrightarrow x = 5$ và $1 - x = 0 \Leftrightarrow x = 1.$

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \ge 0 \Leftrightarrow x \in \left[ {0;1} \right) \cup \left[ {3;5} \right).$

Ta có $f\left( x \right) = \dfrac{{4x - 12}}{{{x^2} - 4x}} = \dfrac{{4x - 12}}{{x\left( {x - 4} \right)}}.$

Phương trình $4x - 12 = 0 \Leftrightarrow x = 3;\,\,x = 0$ và $x - 4 = 0 \Leftrightarrow x = 4.$

Bảng xét dấu

Dựa vào bảng xét dấu, suy ra $f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left[ {3;4} \right).$

Ta có $f\left( x \right) = 1 - \dfrac{{2 - x}}{{3x - 2}} = \dfrac{{3x - 2 - 2 + x}}{{3x - 2}} = \dfrac{{4x - 4}}{{3x - 2}}.$

Phương trình $4x - 4 = 0 \Leftrightarrow x = 1$ và $3x - 2 = 0 \Leftrightarrow x = \dfrac{2}{3}.$

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \le 0 \Leftrightarrow x \in \left( {\dfrac{2}{3};1} \right].$

Ta có $f\left( x \right) =  - \dfrac{4}{{3x + 1}} - \dfrac{3}{{2 - x}} = \dfrac{3}{{x - 2}} - \dfrac{4}{{3x + 1}} = \dfrac{{5x + 11}}{{\left( {x - 2} \right)\left( {3x + 1} \right)}}.$

Phương trình $5x + 11 = 0 \Leftrightarrow x =  - \dfrac{{11}}{5};\,\,x - 2 = 0 \Leftrightarrow x = 2$

và $3x + 1 = 0 \Leftrightarrow x =  - \dfrac{1}{3}.$

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \dfrac{{11}}{5}; - \dfrac{1}{3}} \right) \cup \left( {2; + \,\infty } \right).$

ĐKXĐ: $x \ne  - 1$

$\begin{array}{l}\left| {\dfrac{{3x - 9}}{{x + 1}}} \right| \ge 1 \Leftrightarrow \dfrac{{9{x^2} - 54x + 81}}{{{x^2} + 2x + 1}} \ge 1 \Leftrightarrow \dfrac{{8{x^2} - 56x + 80}}{{{{\left( {x + 1} \right)}^2}}} \ge 0\\ \Leftrightarrow 8{x^2} - 56x + 80 \ge 0\;\;\left( {do\;\;{{\left( {x + 1} \right)}^2} > 0\;\;\forall x \ne 1} \right)\\ \Leftrightarrow 8\left( {x - 5} \right)\left( {x - 2} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 5\\x \le 2\end{array} \right..\end{array}$            

Vậy tập nghiệm của bất phương trình là: $\left( { - \infty ;2} \right] \cup \left[ {5; + \infty } \right)\backslash \left\{ { - 1} \right\}.$

Ta có $f\left( x \right) = \dfrac{1}{x} + \dfrac{2}{{x + 4}} - \dfrac{3}{{x + 3}} < 0 \Leftrightarrow \dfrac{{x + 12}}{{x\left( {x + 3} \right)\left( {x + 4} \right)}} < 0.$

Phương trình $x + 12 = 0 \Leftrightarrow x =  - 12;$

$\,x + 3 = 0 \Leftrightarrow x =  - \,3$ và $x + 4 = 0 \Leftrightarrow x =  - \,4.$

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow x \in \left( { - 12; - \,4} \right) \cup \left( { - \,3;0} \right).$

Ta có $1 - f\left( x \right) = 1 - \dfrac{{\left( {x - 3} \right)\left( {x + 2} \right)}}{{{x^2} - 1}} = 1 - \dfrac{{{x^2} - x - 6}}{{{x^2} - 1}} = \dfrac{{x + 5}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.$

Phương trình $x + 5 = 0 \Leftrightarrow x =  - \,5;\,\,x - 1 = 0 \Leftrightarrow x = 1$ và $x + 1 = 0 \Leftrightarrow x =  - \,1.$

Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $1 - f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \,5; - \,1} \right) \cup \left( {1; + \,\infty } \right).$

Vậy có tất cả $3$ giá trị nguyên âm của $m$ thỏa mãn yêu cầu bài toán.

Phương trình $x + 4 = 0 \Leftrightarrow x =  - \,4$ và $x + 5 = 0 \Leftrightarrow x =  - \,5.$

Phương trình $x - 4 = 0 \Leftrightarrow x = 4$ và $5x - 25 = 0 \Leftrightarrow x - 5 = 0 \Leftrightarrow x = 5.$

Đáp án A: Bảng xét dấu :

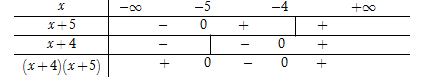
Từ bảng biến thiên ta thấy: $\left( {x + 4} \right)\left( {x + 5} \right) < 0$ $\Leftrightarrow  - 5 < x <  - 4$ hay tập nghiệm của bất phương trình là $S = \left( { - 5; - 4} \right)$ (loại).

Đáp án B: Bảng xét dấu :

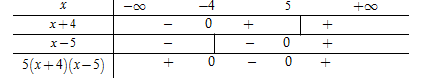
Từ bảng biến thiên ta thấy: $\left( {x + 4} \right)\left( {5x - 25} \right) < 0$ $\Leftrightarrow  - 4 < x < 5$ hay tập nghiệm của bất phương trình là $S = \left( { - 4;5} \right)$ (thỏa mãn).

Dễ dàng kiểm tra các đáp án C, D đều sai

Đặt $f\left( x \right) = \left( {x + 3} \right)\left( {x - 1} \right)$

Phương trình $x + 3 = 0 \Leftrightarrow x =  - \,3$ và $x - 1 = 0 \Leftrightarrow x = 1.$

Ta có bảng xét dấu

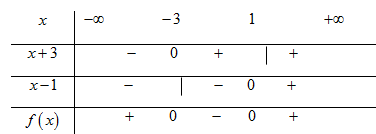
Từ bảng xét dấu ta có $\left( {x + 3} \right)\left( {x - 1} \right) \le 0 \Leftrightarrow  - \,3 \le x \le 1 \Leftrightarrow x \in \left[ { - 3;\,1} \right].$

Suy ra các nghiệm nguyên của bất phương trình là $- 3,\, - 2,\, - 1,\,0,\,1.$

Suy ra tổng các nghiệm nguyên của bất phương trình bằng $- \,5.$

Phương trình $x + 3 = 0 \Leftrightarrow x =  - \,3;\,\,$$x - 3 = 0 \Leftrightarrow x = 3.$

Và $x - 5 = 0 \Leftrightarrow x = 5;\,\,$$14 - 2x = 0 \Leftrightarrow x = 7.$

Ta có bảng xét dấu:

Đáp án A

Từ bảng xét dấu ta thấy, tập nghiệm của bất phương trình $\left( {x + 3} \right)\left( {x - 5} \right)\left( {14 - 2x} \right) \le 0$ là $S = \left[ { - 3;5} \right] \cup \left[ {7; + \infty } \right)$ (loại).

Đáp án B:

Từ bảng xét dấu ta thấy tập nghiệm $S = \left( { - \infty ;3} \right) \cup \left( {5;7} \right)$ là tập nghiệm của bất phương trình $\left( {x - 3} \right)\left( {x - 5} \right)\left( {14 - 2x} \right) > 0.$