Góc lượng giác và cung lượng giác

Trên đường tròn lượng giác gốc A, bốn điểm chính giữa bốn cung phần tư thứ $\left( I \right),\left( {II} \right),\left( {III} \right),\left( {IV} \right)$ biểu diễn các cung lượng giác có số đo $\dfrac{\pi }{4} + k\dfrac{\pi }{2}$. 

Ta có: $0 \le \dfrac{\pi }{6} + k\dfrac{\pi }{5} \le 2\pi$$\Leftrightarrow  - \dfrac{5}{6} \le k \le \dfrac{{55}}{6}$$\Rightarrow k \in \left\{ {0;1;2;...;9} \right\}$.

=>Có 10 giá trị nguyên của $k.$

Vậy có 10 điểm M trên đường tròn lượng giác.

$\sin \alpha  = 1 \Rightarrow \alpha  = \dfrac{\pi }{2} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right).$ 

Trên đường tròn lượng giác (gốc $A$), cung lượng giác có số đo $\alpha  =  - {90^0} + k{360^0}\,\,\,(k \in Z)$ có điểm cuối trùng với điểm $B'$

Ta có điểm đầu là A $\left( {{0^o}} \right)$ và cứ ${90^o} = \dfrac{\pi }{2}$ là góc đó lại quét đến điểm B, A’ ,B’.

$\Rightarrow$ Số đo của cung lượng giác đó là $\dfrac{{k\pi }}{2},\,\,k \in \mathbb{Z}.$ 

Nếu một cung lượng giác có số đo ${a^0}$ (hay $\alpha \,rad$) thì mọi cung lượng giác có cùng điểm đầu và điểm cuối với cung lượng giác đã cho đều có số đo dạng ${a^0} + k{360^0}$ hoặc $\alpha  + k2\pi$.

Do đó số đo của một cung lượng giác có thể âm, có thể dương, có thể nằm trong đoạn $\left[ {0;2\pi } \right]$ cũng có thể không.

 Nói chung số đo của một cung lượng giác là một số thực.

Cung lượng giác có đầu mút trùng với $B$ hoặc $B'$ nghĩa là có hai điểm biểu diễn, do đó số đo có dạng $\alpha  + \dfrac{{k2\pi }}{2} = \alpha  + k\pi$ hoặc $a + k{180^0}$. Loại A, B, C.

Ngoài ra số đo cung $AB'$ bằng $- {90^0}$ nên ta được $a =  - {90^0} + k{180^0}$.

*$\dfrac{{6\pi }}{5} = \dfrac{\pi }{5} + \pi$ nên loại A.

*$- \dfrac{{11\pi }}{5} =  - \dfrac{\pi }{5} - 2\pi$ nên loại B.

*$\dfrac{{9\pi }}{5} = \dfrac{{4\pi }}{5} + \pi$ nên loại C.

*$\dfrac{{31\pi }}{5} = \dfrac{\pi }{5} + 6\pi$ nên chọn D

Ta có: $19 < a < 27$ $\Leftrightarrow 19 < \dfrac{\pi }{3} + k2\pi  < 27$ $\Leftrightarrow 19 - \dfrac{\pi }{3} < k2\pi  < 27 - \dfrac{\pi }{3}$ $\Leftrightarrow \dfrac{{57 - \pi }}{{6\pi }} < k < \dfrac{{81 - \pi }}{{6\pi }}$ $\Rightarrow 2,85 < k < 4,13$.

Mà $k \in \mathbb{Z}$ nên $k \in \left\{ {3;4} \right\}$.

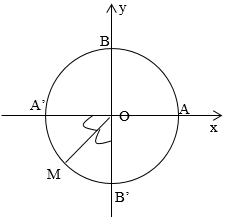
Cung $\alpha$ có mút đầu là $A$ và mút cuối là $M$ theo chiều dương có số đo là $\dfrac{{5\pi }}{4} + k2\pi$ nên loại A,C.

Cung $\alpha$ có mút đầu là $A$ và mút cuối là $M$ theo chiều âm có số đo là $- \dfrac{{3\pi }}{4}$ và chỉ có duy nhất một điểm $M$ trên đường tròn lượng giác nên loại B.

Ta có: $sd\left( {Ox,Ov} \right) - sd\left( {Ox,Ou} \right)$ $=  - \dfrac{\pi }{2} + n2\pi  - \left( { - \dfrac{{5\pi }}{2} + m2\pi } \right)$

$= 2\pi  + \left( {n - m} \right)2\pi  = \left( {n - m + 1} \right)2\pi  = k2\pi$

Do đó $Ou$ và $Ov$ trùng nhau.

Ta có $sd\left( {Ox,Oz} \right) = - \dfrac{{63\pi }}{2} = \dfrac{\pi }{2} - \dfrac{{64\pi }}{2}$ $= \dfrac{\pi }{2} - 32\pi$ nên hai tia $Ox$ và $Oz$ vuông góc.

Ta có: $sd\left( {Ox,Ou} \right) - sd\left( {Ox,Ov} \right)$ $= {45^0} + m{360^0} - \left( { - {{135}^0} + n{{360}^0}} \right)$ $= {180^0} + \left( {m - n} \right){360^0} = {180^0} + k{360^0}$

$\left( {Ox,Ov} \right) =  - {135^{\rm{o}}} + n{360^{\rm{o}}} = {225^{\rm{o}}} + k{360^{\rm{o}}} = {45^{\rm{o}}} + {180^{\rm{o}}} + k{360^{\rm{o}}}$$\left( {n \in \mathbb{Z}} \right)$.

Vậy, Ta có hai tia $Ou$ và $Ov$ đối nhau

Ta có: $- \dfrac{{7\pi }}{4} = \dfrac{\pi }{4} - 2\pi$; $\dfrac{{13\pi }}{4} = \dfrac{{5\pi }}{4} + 2\pi$; $- \dfrac{{5\pi }}{4} = \dfrac{{3\pi }}{4} - 2\pi$.

Suy ra chỉ có hai cung $\dfrac{\pi }{4}$ và $- \dfrac{{7\pi }}{4}$có điểm cuối trùng nhau.

Theo giả thiết ta có số đo cung $AM$ bằng $\dfrac{{25\pi }}{4} = \dfrac{\pi }{4} + 6\pi$, suy ra điểm $M$ trùng với điểm cuối của góc lượng giác $\dfrac{\pi }{4}$ hay nó là điểm chính giữa của cung phần tư thứ ${\rm{I}}$.

Do $sdAM = \dfrac{\pi }{3} + \dfrac{{k\pi }}{3} = \dfrac{{k2\pi }}{6}$ nên có $6$ điểm biểu diễn cung lượng giác $\dfrac{\pi }{3} + \dfrac{{k\pi }}{3}$.

Cụ thể:

$k = 0,sdAM = \dfrac{\pi }{3}$; $k = 1,sdAM = \dfrac{{2\pi }}{3}$; $k = 2,sdAM = \dfrac{{3\pi }}{3}$; $k = 3,sdAM = \dfrac{{4\pi }}{3}$; $k = 4,sdAM = \dfrac{{5\pi }}{3}$;$k = 5,sdAM = 2\pi$; $k = 6,sdAM = \dfrac{{7\pi }}{3}$.

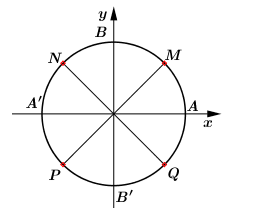
Số đo cung $AM = {45^0} = \dfrac{\pi }{4}$. Ngoài ra có bốn điểm biểu diễn tạo thành một hình vuông nên $\alpha  = \dfrac{\pi }{4} + \dfrac{{k2\pi }}{4} = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}$.

Đường tròn định hướng là đường tròn trên đó ta đã chọn một chiều chuyển động gọi là chiều dương và chiều ngược lại được gọi là chiều âm là một đường tròn định hướng.

Chiều dương của đường tròn định hướng được quy ước là ngược chiều kim đồng hồ.

Với hai điểm $A,B$ trên đường tròn định hướng xác định vô số góc lượng giác tia đầu $OA$, tia cuối $OB$.