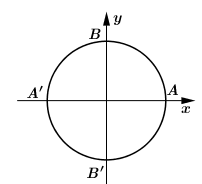
Chọn điểm $A\left( {1;0} \right)$ làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối $M$ của cung lượng giác có số đo \(\dfrac{{25\pi }}{4}\).

Trên đường tròn lượng giác gốc \(A,\)  bốn điểm chính giữa bốn cung phần tư thứ \(\left( I \right),\left( {II} \right),\left( {III} \right),\left( {IV} \right)\) biểu diễn các cung lượng giác có số đo nào sau đây?

Trên đường tròn lượng giác gốc \(A,\)  có bao nhiêu điểm \(M\)  thỏa mãn số đo cung lượng giác  bằng \(\dfrac{\pi }{6} + k\dfrac{\pi }{5},\) với \(k\) là số nguyên.

Trên đường tròn lượng giác (gốc \(A\)), cung lượng giác có số đo \(\alpha  =  - {90^0} + k{360^0}\,\,\,(k \in Z)\) có điểm cuối trùng với điểm nào sau đây ?

Trên đường tròn lượng giác gốc \(A\), số đo của cung lượng giác nào sau đây có các điểm biểu diễn là cả bốn điểm \(A,{\rm{ }}A',{\rm{ }}B,{\rm{ }}B'\) như hình dưới đây ? 

Tìm mệnh đề đúng trong các mệnh đề sau:

Cung lượng giác nào sau đây có mút trùng với \(B\) hoặc \(B'\)