Trả lời bởi giáo viên
Đáp án đúng: d
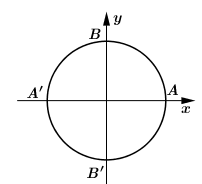
Cung lượng giác có đầu mút trùng với \(B\) hoặc \(B'\) nghĩa là có hai điểm biểu diễn, do đó số đo có dạng \(\alpha + \dfrac{{k2\pi }}{2} = \alpha + k\pi \) hoặc \(a + k{180^0}\). Loại A, B, C.
Ngoài ra số đo cung \(AB'\) bằng \( - {90^0}\) nên ta được \(a = - {90^0} + k{180^0}\).
Hướng dẫn giải:
Sử dụng lý thuyết: Cung lượng giác có số đo \(\alpha + \dfrac{{k2\pi }}{n}\) (hoặc \(a + \dfrac{{k{{360}^0}}}{n}\)) thì có \(n\) điểm biểu diễn.