Cho \(f\left( x \right) = a{x^2} + bx + c\,{\rm{ }}\left( {a \ne 0} \right).\) Điều kiện để \(f\left( x \right) > 0\,,{\rm{ }}\forall x \in \mathbb{R}\) là
Ta có:
\(f\left( x \right) > 0\,,{\rm{ }}\forall x \in \mathbb{R}\) khi \(a > 0\) và \(\Delta < 0\).
Tìm m để bất phương trình \(2m{x^2} - 2\left( {m + 1} \right)x + m + 1 \le 0\) có nghiệm
Ta tìm m để bất phương trình vô nghiệm.
Bất phương trình \(2m{x^2} - 2\left( {m + 1} \right)x + m + 1 \le 0\) vô nghiệm
\(\begin{array}{l} \Leftrightarrow 2m{x^2} - 2\left( {m + 1} \right)x + m + 1 > 0\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta ' < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\{\left( {m + 1} \right)^2} - 2m\left( {m + 1} \right) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\left( {m + 1} \right)\left( {1 - m} \right) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m > 1\\m < - 1\end{array} \right.\end{array} \right. \Leftrightarrow m > 1\end{array}\)
Vậy bất phương trình đã cho có nghiệm khi \(m \le 1\)
Tam thức \(f\left( x \right) = - {x^2} - 2x + 3\) nhận giá trị dương khi và chỉ khi:
\(\begin{array}{l}f\left( x \right) = - {x^2} - 2x + 3 > 0 \Leftrightarrow {x^2} + 2x - 3 < 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 3} \right) < 0 \Leftrightarrow - 3 < x < 1.\end{array}\)
Với giá trị nào của m để phương trình \(\left( {m - 1} \right){x^2} + \left( {2m + 1} \right)x + m - 5 = 0\) có 2 nghiệm trái dấu:
Phương trình \(\left( {m - 1} \right){x^2} + \left( {2m + 1} \right)x + m - 5 = 0\) có hai nghiệm trái dấu
\( \Leftrightarrow \left( {m - 1} \right)\left( {m - 5} \right) < 0 \Leftrightarrow 1 < m < 5.\)
Phương trình \(\left( {m - 1} \right){x^2} + \left( {2m + 1} \right)x + m - 5 = 0\) có hai nghiệm trái dấu
\( \Leftrightarrow \left( {m - 1} \right)\left( {m - 5} \right) < 0 \Leftrightarrow 1 < m < 5.\)
Cho phương trình \({x^2} + 2x - {m^2} = 0.\) Biết rằng có hai giá trị \({m_1},\,\,{m_2}\) của tham số m để phương trình có hai nghiệm \({x_1},\,\,{x_2}\) thỏa mãn \(x_1^3 + x_2^3 + 10 = 0.\) Tính \({m_1}.{m_2}.\)
Phương trình đã cho có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)
\( \Leftrightarrow 1 + {m^2} > 0\,\,\,\forall m\)
\( \Rightarrow \) Phương trình đã cho luôn có hai nghiệm phân biệt \({x_1},\,{x_2}\) với mọi m.
Áp dụng định lý Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\\{x_1}{x_2} = - {m^2}\end{array} \right..\)
Theo đề bài ta có: \(x_1^3 + x_2^3 + 10 = 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right) + 10 = 0\\ \Leftrightarrow {\left( { - 2} \right)^3} - 3\left( { - {m^2}} \right)\left( { - 2} \right) + 10 = 0\\ \Leftrightarrow - 8 - 6{m^2} + 10 = 0\\ \Leftrightarrow 6{m^2} = 2 \Leftrightarrow {m^2} = \dfrac{1}{3}\\ \Leftrightarrow \left[ \begin{array}{l}{m_1} = - \dfrac{1}{{\sqrt 3 }}\\{m_2} = \dfrac{1}{{\sqrt 3 }}\end{array} \right. \Rightarrow {m_1}{m_2} = - \dfrac{1}{{\sqrt 3 }}.\dfrac{1}{{\sqrt 3 }} = - \dfrac{1}{3}.\end{array}\)
\(f\left( x \right) < 0 \Leftrightarrow -2{x^2} + \left( {m + 2} \right)x + m-4\)
Ta có: \(\Delta = {\left( {m + 2} \right)^2} + 8\left( {m - 4} \right) = {m^2} + 12m - 28.\)
\(\begin{array}{l} \Rightarrow f\left( x \right) < 0\,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 < 0\,\,\forall m\\{m^2} + 12m - 28 < 0\end{array} \right.\\ \Leftrightarrow \left( {m - 2} \right)\left( {m + 14} \right) < 0 \Leftrightarrow - 14 < m < 2.\end{array}\)
Vậy với \(m \in \left( { - 14;2} \right)\) thỏa mãn yêu cầu đề bài.
Phương trình \({x^2} + mx + 2m - 3 = 0\) có hai nghiệm phân biệt
\( \Leftrightarrow \Delta > 0 \Leftrightarrow {m^2} - 4\left( {2m - 3} \right) > 0 \Leftrightarrow {m^2} - 8m + 12 > 0 \Leftrightarrow \left( {m - 2} \right)\left( {m - 6} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}m < 2\\m > 6\end{array} \right.\)
Bất phương trình:\(\left( {2m + 1} \right){x^2} - 3\left( {m + 1} \right)x + m + 1 > 0\) vô nghiệm
\( \Leftrightarrow \left( {2m + 1} \right){x^2} - 3\left( {m + 1} \right)x + m + 1 \le 0\) có nghiệm với mọi \(m\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}2m + 1 < 0\\\Delta = 9{\left( {m + 1} \right)^2} - 4\left( {2m + 1} \right)\left( {m + 1} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < - \dfrac{1}{2}\\9{m^2} + 18m + 9 - 8{m^2} - 12m - 4 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < - \dfrac{1}{2}\\{m^2} + 6m + 5 \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < - \dfrac{1}{2}\\\left( {m + 1} \right)\left( {m + 5} \right) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < - \dfrac{1}{2}\\ - 5 \le m \le - 1\end{array} \right. \Leftrightarrow - 5 \le m \le - 1.\end{array}\)
Bất phương trình: \({x^2} - 2mx + 2m + 3 \ge 0\) có nghiệm đúng \(\forall x \in \mathbb{R}\)
\( \Leftrightarrow \Delta ' = {m^2} - 2m - 3 \le 0 \Leftrightarrow - 1 \le m \le 3\)
Hàm số \(f\left( x \right) = {x^2} - 2x - 3\) nhận giá trị dương khi và chỉ khi
Hàm số \(f\left( x \right)\) nhận giá trị dương \( \Leftrightarrow f\left( x \right) > 0\).
Giải: \(f\left( x \right) = {x^2} - 2x - 3 = 0\)\( \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right.\)
Ta có bảng xét dấu:
![]()
\( \Rightarrow f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 3\end{array} \right.\)
Vậy \(x \in \left( { - \infty ;\,\, - 1} \right) \cup \left( {3;\,\, + \infty } \right)\) thì hàm số \(f\left( x \right)\) nhận giá trị dương.
Tập xác định của hàm số \(y = x + \sqrt {{x^2} + 4x - 5} \) là
Hàm số \(y = x + \sqrt {{x^2} + 4x - 5} \)
ĐKXĐ: \({x^2} + 4x - 5 \ge 0\)
\( \Leftrightarrow \left( {x - 1} \right)\left( {x + 5} \right) \ge 0\) \( \Leftrightarrow \left[ \begin{array}{l}x \le - 5\\x \ge 1\end{array} \right.\)
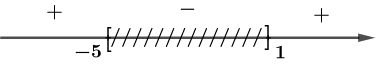
Vậy tập xác định của hàm số \(y = x + \sqrt {{x^2} + 4x - 5} \) là \(D = \left( { - \infty ;\,\, - 5} \right] \cup \left[ {1;\,\, + \infty } \right)\).
Giá trị của tham số \(m\) để phương trình \({x^2} - \left( {m - 1} \right)x + m + 2 = 0\) có nghiệm là
Vì \(a = 1 \ne 0\) nên phương trình \({x^2} - \left( {m - 1} \right)x + m + 2 = 0\) có nghiệm khi và chỉ khi \(\Delta \ge 0 \Leftrightarrow {\left( {m - 1} \right)^2} - 4\left( {m + 2} \right) \ge 0\)\( \Leftrightarrow {m^2} - 6m - 7 \ge 0\)\( \Leftrightarrow \left[ \begin{array}{l}m \le - 1\\m \ge 7\end{array} \right.\)\( \Rightarrow m \in \left( { - \infty ;\,\, - 1} \right] \cup \left[ {7;\,\, + \infty } \right)\)
Vậy \(m \in \left( { - \infty ;\,\, - 1} \right] \cup \left[ {7;\,\, + \infty } \right)\)
Cho phương trình: \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 4m + 3 = 0\,\,\,\,\,\left( * \right)\). Tìm \(m\) để phương trình \(\left( * \right)\) có hai nghiệm trái dấu.
Phương trình \(\left( * \right)\) có hai nghiệm trái dấu \( \Leftrightarrow P < 0\)\( \Leftrightarrow {m^2} - 4m + 3 < 0\)\( \Leftrightarrow 1 < m < 3\)
Tìm tất cả các giá trị thực của \(m\) để phương trình \(m{x^2} + 2\left( {m + 3} \right)x + m = 0\) có hai nghiệm phân biệt cùng dấu.
Phương trình \(m{x^2} + 2\left( {m + 3} \right)x + m = 0\) có hai nghiệm phân biệt cùng dấu khi và chỉ khi
\(\left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\\P > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{\left( {m + 3} \right)^2} - {m^2} > 0\\\dfrac{m}{m} > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\6m + 9 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m > - \dfrac{3}{2}\end{array} \right.\)
Vậy \(m > - \dfrac{3}{2}\) và \(m \ne 0\).
Phương trình \(\left( {m - 1} \right){x^2} - 3mx + m - 2 = 0\) vô nghiệm khi
\(\left( {m - 1} \right){x^2} - 3mx + m - 2 = 0\,\,\,\left( * \right)\)
+) Với \(m - 1 = 0 \Leftrightarrow m = 1\), phương trình \(\left( * \right)\) trở thành: \( - 3x - 1 = 0 \Leftrightarrow x = - \dfrac{1}{3}\)
\( \Rightarrow m = 1\) thì phương trình \(\left( * \right)\) có nghiệm \(x = - \dfrac{1}{3}\) \(\left( 1 \right)\)
+) Với \(m - 1 \ne 0 \Leftrightarrow m \ne 1\), phương trình \(\left( * \right)\) vô nghiệm
\( \Leftrightarrow \Delta < 0\)
\(\begin{array}{l} \Leftrightarrow 9{m^2} - 4\left( {m - 1} \right)\left( {m - 2} \right) < 0\\ \Leftrightarrow 9{m^2} - 4{m^2} + 12m - 8 < 0\\ \Leftrightarrow 5{m^2} + 12m - 8 < 0\\ \Leftrightarrow \dfrac{{ - 6 - 2\sqrt {19} }}{5} < m < \dfrac{{ - 6 + 2\sqrt {19} }}{5}\,\,\,\left( 2 \right)\end{array}\)
Kết hợp \(\left( 1 \right)\) và \(\left( 2 \right)\), bất phương trình \(\left( * \right)\) vô nghiệm khi và chỉ khi \(\dfrac{{ - 6 - 2\sqrt {19} }}{5} < m < \dfrac{{ - 6 + 2\sqrt {19} }}{5}\).
Phương trình \(\left( {m - 1} \right){x^2} - 2x + m + 1 = 0\) có hai nghiệm phân biệt khi
Phương trình \(\left( {m - 1} \right){x^2} - 2x + m + 1 = 0\) có hai nghiệm phân biệt khi và chỉ khi
\(\left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ne 0\\{\left( { - 1} \right)^2} - \left( {m - 1} \right)\left( {m + 1} \right) > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\ - {m^2} + 2 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\ - \sqrt 2 < m < \sqrt 2 \end{array} \right.\)
\( \Rightarrow m \in \left( { - \sqrt 2 ;\,\,\sqrt 2 } \right)\backslash \left\{ 1 \right\}\)
Tìm m để phương trình \(\left( {m - 3} \right){x^2} + 2mx + 3 - m = 0\) có 2 nghiệm trái dấu.
Để phương trình \(\left( {m - 3} \right){x^2} + 2mx + 3 - m = 0\) có 2 nghiệm trái dấu
\( \Leftrightarrow \left( {m - 3} \right)\left( {3 - m} \right) < 0 \Leftrightarrow - \left( {m - 3} \right) < 0 \Leftrightarrow m - 3 \ne 0 \Leftrightarrow m \ne 3.\)
Điều kiện của \(m\) để phương trình \({x^2} - mx + 1 = 0\) có hai nghiệm âm phân biệt là
Phương trình \({x^2} - mx + 1 = 0\) có hai nghiệm âm phân biệt khi và chỉ khi
\(\left\{ \begin{array}{l}\Delta > 0\\P > 0\\S < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4 > 0\\1 > 0\\m < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m < - 2\\m > 2\end{array} \right.\\m < 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m < - 2\\m < 0\end{array} \right.\\\left\{ \begin{array}{l}m > 2\\m < 0\end{array} \right.\end{array} \right.\)\( \Leftrightarrow m < - 2\)
Có bao nhiêu giá trị nguyên của \(m\) thuộc đoạn \(\left[ { - 10;\,\,10} \right]\) để phương trình \({x^2} - mx + 3m = 0\) vô nghiệm?
Phương trình \({x^2} - mx + 3m = 0\) vô nghiệm khi và chỉ khi \(\Delta < 0\).
\( \Leftrightarrow {m^2} - 12m < 0\)\( \Rightarrow 0 < m < 12\)
Kết hợp với điều kiện \(\left\{ \begin{array}{l}m \in Z\\m \in \left[ { - 10;\,\,10} \right]\end{array} \right.\)\( \Rightarrow m \in \left\{ {1;\,\,2;\,\, \ldots \,\,;\,\,9;\,\,10} \right\}\)
Vậy có \(10\) giá trị nguyên của \(m\) thỏa mãn.
Có bao giá trị nguyên của m trong đoạn \(\left[ { - 2020;2020} \right]\) để tam thức bậc hai \(( - {m^2} + 4){x^2} + 2(m + 2)x -2\) luôn âm?
Ta có
\(\begin{array}{l}( - {m^2} + 4){x^2} + 2(m + 2)x - 2 < 0\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l} - {m^2} + 4 < 0\\\Delta ' < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\\{\left( {m + 2} \right)^2} + 2\left( { - {m^2} + 4} \right) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\\{m^2} - 4m - 12 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < - 2\end{array} \right.\\\left[ \begin{array}{l}m > 6\\m < - 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m > 6\\m < - 2\end{array} \right.\end{array}\)
Ta có \( - 2020 \le m \le 2020\) nên \(\left[ \begin{array}{l} - 2020 \le m < - 2\\6 < m \le 2020\end{array} \right.\)
Vì m nguyên nên \(m \in \left\{ { - 2020; - 2019;...; - 3} \right\} \cup \left\{ {7;8;...;2020} \right\}\)
Do đó có \(\left[ { - 3 - ( - 2020) + 1} \right] = 2018\) số nguyên từ \( - 2020\) đến -3 và có \(2020 - 7 + 1 = 2014\) số nguyên từ 7 đến 2020.
Vậy có 4032 số nguyên thỏa mãn.

