Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}\left( {x - 2} \right)\left( {{x^2} + 5x + 4} \right) < 0\\{x^2} - 2x - 15 > 0\end{array} \right.\) là
\(\begin{array}{l}\left\{ \begin{array}{l}\left( {x - 2} \right)\left( {{x^2} + 5x + 4} \right) < 0\\{x^2} - 2x - 15 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 2} \right)\left( {x + 1} \right)\left( {x + 4} \right) < 0(1)\\\left( {x + 3} \right)\left( {x - 5} \right) > 0(2)\end{array} \right.\end{array}\)
Đặt \(f\left( x \right) = \left( {x + 4} \right)\left( {x + 1} \right)\left( {x - 2} \right)\)
Bảng xét dấu của (1)

Từ bảng biến thiên ta có tập nghiệm của (1) là \({S_1} = \left( { - \infty ; - 4} \right) \cup \left( { - 1;2} \right)\)
Tập nghiệm của bất phương trình (2) là \({S_2} = \left( { - \infty ; - 3} \right) \cup \left( {5; + \infty } \right)\)
Ta biểu diễn các tập nghiệm trên trục số ( phần gạch chéo màu đen là phần bù của \({S_1}\), phần gạch chéo màu xanh là phần bù của \({S_2}\))

Phần không bị gạch chéo là \(S = {S_1} \cap {S_2}\)
Vậy tập nghiệm của hệ là \(S = \left( { - \infty ; - 4} \right)\).
Cho \(f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) \le 0\,,\forall x \in \mathbb{R}\) là
Ta có:
\(f\left( x \right) \le 0\,,{\rm{ }}\forall x \in \mathbb{R}\) khi \(a < 0\) và \(\Delta \le 0\).
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). Biết rằng \(a < 0\,\,;\,\,\Delta = {b^2} - 4ac < 0\). Mệnh đề nào sau đây đúng ?
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\). Biết rằng \(a < 0\,\,;\,\,\Delta = {b^2} - 4ac < 0\)
\( \Rightarrow f\left( x \right) < 0,\,\,\forall x \in \mathbb{R}\)
Phương trình \({x^2} - 2mx + 3m - 2 = 0\) có nghiệm
\( \Leftrightarrow \Delta ' = {\left( { - m} \right)^2} - \left( {3m - 2} \right) \ge 0\) \( \Leftrightarrow {m^2} - 3m + 2 \ge 0 \Leftrightarrow \left[ \begin{array}{l}m \ge 2\\m \le 1\end{array} \right.\)
Biết rằng tập xác định của hàm số \(y = \sqrt {{x^2} + x - 2} + \dfrac{1}{{\sqrt x }}\) là \(D = \left[ {a; + \infty } \right)\). Khẳng định nào sau đây đúng?
\(y = \sqrt {{x^2} + x - 2} + \dfrac{1}{{\sqrt x }}\)
ĐKXĐ: \(\left\{ \begin{array}{l}{x^2} + x - 2 \ge 0\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le - 2\\x \ge 1\end{array} \right.\\x > 0\end{array} \right. \Leftrightarrow x \ge 1\)
Vậy \(a = 1 > 0.\)
Để bất phương trình \(m{x^2} - 4x + m < 0\) vô nghiệm
\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\Delta ' = {2^2} - {m^2} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\{m^2} \ge 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m \ge 2\\m \le - 2\end{array} \right.\end{array} \right. \Leftrightarrow m \ge 2\)
Mà \(m \in \left[ { - 10;10} \right] \Rightarrow m \in \left[ {2;10} \right]\)
Vậy có 9 giá trị nguyên của m thỏa mãn yêu cầu đề bài.
test 2
sdgasdg
Hàm số xác định \( \Leftrightarrow \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 3\left( {m - 2} \right) \ge 0\)
TH1 : Với \(m = 1 \Rightarrow y = \sqrt { - 4x - 3} \) xác định khi \(x \le - \dfrac{3}{4} \ne \mathbb{R} \Rightarrow \) Loại
TH2 : Với \(m \ne 1\).
Hàm số \(y = \sqrt {\left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 3\left( {m - 2} \right)} \) có tập xác định là \(D = \mathbb{R}\)
\(\begin{array}{l} \Leftrightarrow \left( {m - 1} \right){x^2} - 2\left( {m + 1} \right)x + 3\left( {m - 2} \right) \ge 0\;\;\forall x\\ \Leftrightarrow \left\{ \begin{array}{l}m - 1 > 0\\\Delta ' = {\left( {m + 1} \right)^2} - 3\left( {m - 1} \right)\left( {m - 2} \right) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 1\\{m^2} + 2m + 1 - 3{m^2} + 9m - 6 \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 1\\ - 2{m^2} + 11m - 5 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 1\\\left( {m - 5} \right)\left( {2m - 1} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 1\\\left[ \begin{array}{l}m \ge 5\\m \le \dfrac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m \ge 5.\end{array}\)
Vậy với \(m \ge 5\) thỏa mãn yêu cầu đề bài.
Hàm số có kết quả xét dấu

là hàm số:
Dễ thấy hàm số có dạng \(f\left( x \right) = a{x^2} + bx + c\) có hai nghiệm \({x_1} = - 2,\;{x_2} = 3\)
Ta thấy trong khoảng hai nghiệm \(\left( { - 2;\;3} \right)\) thì \(f\left( x \right) > 0 \Rightarrow \) hệ số \(a < 0\) \( \Rightarrow \) Loại A, B
Mặt khác với \(a{x^2} + bx + c = 0\) có hai nghiệm \(x = - 2\) và \(x = 3\) \( \Rightarrow \) Chọn D
Tìm tham số \(m\) để hàm số \(y = \sqrt {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right) + 4} \) có tập xác định là \(D = \mathbb{R}\)?
Hàm số \(y = \sqrt {\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4} \) có tập xác định là \(D = \mathbb{R}\) khi và chỉ khi \(\left( {m + 1} \right){x^2} - 2\left( {m + 1} \right)x + 4 \ge 0\) với mọi \(x \in \mathbb{R}\).
TH1: $m\ne -1$
\(\begin{array}{l} \left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 1 > 0\\4{\left( {m + 1} \right)^2} - 16\left( {m + 1} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\4{m^2} - 8m - 12 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 1\\ - 1 \le m \le 3\end{array} \right.\\ \Leftrightarrow - 1 < m \le 3\end{array}\)
TH2: $m=-1$
Khi đó $y=\sqrt{4}=2$
=> Tập xác định của hàm số là $D=\mathbb{R}$
Vậy $- 1 \le m \le 3$
Tập xác định của hàm số \(y = \sqrt {5 - 4x - {x^2}} \) là
Hàm số \(y = \sqrt {5 - 4x - {x^2}} \) xác định khi và chỉ khi \(5 - 4x - {x^2} \ge 0\).
$\Leftrightarrow x^2+4x-5 \le 0\Leftrightarrow (x+5)(x-1) \le 0$$\Leftrightarrow -5 \le x \le 1$
Vậy tập xác định của hàm số \(y = \sqrt {5 - 4x - {x^2}} \) là \(\left[ { - 5;\,\,1} \right]\).
ĐKXĐ: \({x^2} + 4x - 5 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne - 5\end{array} \right.\)
\(\dfrac{{{x^2} - 9}}{{{x^2} + 4x - 5}} \le 0 \Leftrightarrow \dfrac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{\left( {x - 1} \right)\left( {x + 5} \right)}} \le 0\)
Đặt \(f\left( x \right) = \dfrac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{{\left( {x - 1} \right)\left( {x + 5} \right)}}.\) Ta có bảng:

Vậy \(f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - 5; - 3} \right] \cup \left( {1;3} \right].\)
Phương trình \(m\left( {m + 2} \right){x^2} - 2mx + 2 = 0\) có hai nghiệm dương phân biệt
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m\left( {m + 2} \right) \ne 0\\\Delta ' = {m^2} - 2m\left( {m + 2} \right) > 0\\S = \dfrac{{2m}}{{m\left( {m + 2} \right)}} > 0\\P = \dfrac{2}{{m\left( {m + 2} \right)}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - {m^2} - 4m > 0\\\dfrac{{2m}}{{m\left( {m + 2} \right)}} > 0\\m\left( {m + 2} \right) > 0\;\;\left( {do\;2 > 0} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\m\left( {m + 4} \right) < 0\\m > 0\\m + 2 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 2\\ - 4 < m < 0\\m > - 2\\m > 0\end{array} \right. \Rightarrow m \in \emptyset .\end{array}\)
Vậy \(m \in \emptyset .\)
Cho \(f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) \ge 0\,,\,\forall x \in \mathbb{R}\) là
Ta có: \(f\left( x \right) \ge 0\,,{\rm{ }}\forall x \in \mathbb{R}\) khi \(a > 0\) và \(\Delta \le 0\).
Cho \(f\left( x \right) = a{x^2} + bx + c\,\left( {a \ne 0} \right)\). Điều kiện để \(f\left( x \right) < 0\,,\,\forall x \in \mathbb{R}\) là
Ta có: \(f\left( x \right) < 0\,,{\rm{ }}\forall x \in \mathbb{R}\) khi \(a < 0\) và \(\Delta < 0\).
Cho \(f\left( x \right) = a{x^2} + bx + c\left( {a > 0} \right)\) có $\Delta = {b^2} - 4ac \le 0$. Khi đó mệnh đề nào đúng?
Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a > 0} \right)\) có $\Delta = {b^2} - 4ac \le 0$ thì \(f\left( x \right) \ge 0,\forall x \in \mathbb{R}\).
Tam thức bậc hai $f\left( x \right) = - {x^2} + 5x - 6$ nhận giá trị dương khi và chỉ khi
Ta có $f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 3\end{array} \right.$.
Bảng xét dấu
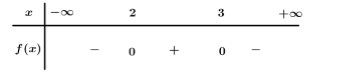
Dựa vào bảng xét dấu $f\left( x \right) > 0 \Leftrightarrow x \in \left( {2;3} \right).$
Tam thức bậc hai $f\left( x \right) = {x^2} + \left( {\sqrt 5 - 1} \right)x - \sqrt 5 $ nhận giá trị dương khi và chỉ khi
Ta có $f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \sqrt 5 \end{array} \right.$.
Bảng xét dấu:
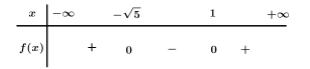
Dựa vào bảng xét dấu $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; - \sqrt 5 } \right) \cup \left( {1; + \infty } \right).$
Tam thức bậc hai \(f\left( x \right) = - {x^2} + 3x - 2\) nhận giá trị không âm khi và chỉ khi
Ta có \(f\left( x \right) = 0\, \Leftrightarrow \,\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\) .
Bảng xét dấu
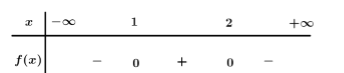
Dựa vào bảng xét dấu \(f\left( x \right) \ge 0\, \Leftrightarrow \,1 \le x \le 2\).
Số giá trị nguyên của \(x\) để tam thức \(f\left( x \right) = 2{x^2} - 7x - 9\) nhận giá trị âm là
Ta có \(f\left( x \right) = 0\, \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \dfrac{9}{2}\end{array} \right.\) . Bảng xét dấu
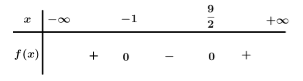
Dựa vào bảng xét dấu \(f\left( x \right) < 0\, \Leftrightarrow \, - 1 < x < \dfrac{9}{2}.\)
Mà \(x\) nguyên nên \(x \in \left\{ {0;1;2;3;4} \right\}\).

