Câu hỏi:
2 năm trước
Biết rằng tập xác định của hàm số \(y = \sqrt {{x^2} + x - 2} + \dfrac{1}{{\sqrt x }}\) là \(D = \left[ {a; + \infty } \right)\). Khẳng định nào sau đây đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
\(y = \sqrt {{x^2} + x - 2} + \dfrac{1}{{\sqrt x }}\)
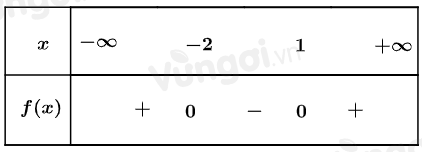
ĐKXĐ: \(\left\{ \begin{array}{l}{x^2} + x - 2 \ge 0\\x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le - 2\\x \ge 1\end{array} \right.\\x > 0\end{array} \right. \Leftrightarrow x \ge 1\)
Vậy \(a = 1 > 0.\)
Hướng dẫn giải:
\(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0\)
\(\dfrac{1}{{g\left( x \right)}}\) xác định \( \Leftrightarrow g\left( x \right) \ne 0\)
Giải thích thêm:
Bảng xét dấu của $f(x)=x^2+x-2$ là