Bất phương trình và hệ bất phương trình bậc nhất hai ẩn

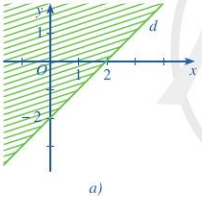
Đường thẳng qua điểm (2;0) và (0;-2) nên phương trình đường thẳng là

x-y-2=0

Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0

=> Bất phương trình cần tìm là \(x - y - 2 \ge 0\)

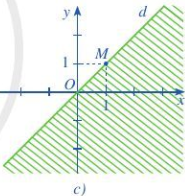
Đường thẳng qua điểm (0;0) và (1;1) nên phương trình đường thẳng là

x-y=0

Lấy điểm (0;1) thuộc miền nghiệm ta có x-y=-1<0

=> Bất phương trình cần tìm là \(x - y \le 0\)

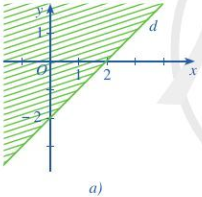
Đường thẳng qua điểm (2;0) và (0;-2) nên phương trình đường thẳng là

x-y-2=0

Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0

=> Bất phương trình cần tìm là \(x - y - 2 \ge 0\)

+) Thay x=10, y=10 ta được

=> (10;10) là nghiệm của bất phương trình

+) Thay x=10, y=20 ta được

=> (10;20) là nghiệm của bất phương trình

+) Thay x=20, y=10 ta được

=> (20;10) là nghiệm của bất phương trình.

Vậy cả 3 cặp số là nghiệm của bất phương trình.

Bước 1: Biểu diễn diện tích x chiếc ghế và y chiếc bàn.

Diện tích của x chiếc ghế là \(0,5x\left( {{m^2}} \right)\) và y chiếc bàn là \(1,2y\left( {{m^2}} \right)\)

Bước 2: Biểu diễn diện tích lưu thông và cho lớn hơn hoặc bằng 12 \({m^2}\).

Tổng diện tích x chiếc ghế và y chiếc bàn là \(0,5x + 1,2y\left( {{m^2}} \right)\)

Diện tích lưu thông là \(60 - 0,5x - 1,2y\left( {{m^2}} \right)\)

Bất phương trình cần tìm là

\(\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}\)

Thay x=0, y=0 vào bất phương trình ta được \(26.0 + 20.0 \ge 46\left( {Sai} \right)\)

Thay x=1, y=1 vào bất phương trình ta được

Thay x=2, y=1 vào bất phương trình ta được

Thay x=1, y=2 vào bất phương trình ta được

Vậy có 3 cặp số thỏa mãn bất phương trình đã cho.

Bước 1: Biểu diễn lượng protein có trong x lạng thịt bò và y lạng cá rô phi.

Lượng protein trong x lạng thịt bò là 26x (g)

Lượng protein trong y lạng cá rô phi là 20y (g)

Lượng protein trong x lạng thịt bò và y lạng cá rô phi là 26x+20y (g).

Bước 2: Biểu diễn bất phương trình.

Vì lượng protein tối thiểu là 46g nên ta có bất phương trình:

\(26x + 20y \ge 46\)

Bước 1: Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}} \right)\). Biểu diễn các đại lượng khác theo \(x\) và \(y\).

Gọi số lượng mũ kiểu thứ nhất và kiểu thứ hai trong một ngày mà phân xưởng cần sản xuất lần lượt là \(x\) và \(y\) \(\left( {x,y \in \mathbb{N}} \right)\).

Theo giả thiết, thị trường tiêu thụ tối đa trong một ngày là 200 chiếc mũ kiểu thứ nhất và 240 chiếc mũ kiểu thứ hai nên ta có \(0 \le x \le 200;0 \le y \le 240\)

Thời gian làm \(y\) chiếc kiểu 2 trong một ngày là \(\dfrac{y}{{60}}\left( h \right)\)

Thời gian để làm ra một chiếc mũ kiểu thứ nhất nhiều gấp hai lần thời gian làm ra một chiếc mũ kiểu thứ hai nên thời gian làm mũ thứ nhất là 1 giờ làm được 30 chiếc.

Thời gian làm \(x\) chiếc kiểu 1 trong một ngày là \(\dfrac{x}{{30}}\left( h \right)\)

Tổng thời gian làm trong một ngày là 8h nên ta có:

\(\dfrac{x}{{30}} + \dfrac{y}{{60}} = 8\)

Bước 2: Lập hệ bất phương trình.

Bước 3: Biểu diễn miền nghiệm.

Miền biểu diễn miền nghiệm là phần màu vàng:

Bước 4: Tìm \(x\) và \(y\) để tiền lãi cao nhất.

Từ miền nghiệm ta thấy tiền lãi cao nhất tại khi điểm \(\left( {x;y} \right)\) là một trong các đỉnh của tam giác màu vàng:

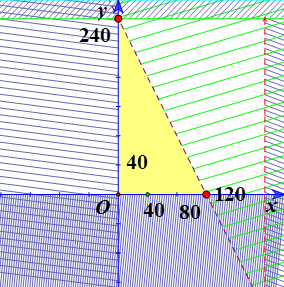
\(T = 24x + 15y\)

\(T\left( {0;240} \right) = 15.240 = 3600\) (nghìn đồng)

\(T\left( {120;0} \right) = 24.120 = 2880\)(nghìn đồng)

Số lượng mũ kiểu 1 là 240 và số lượng mũ kiểu 2 là 0.

Điều kiện: $x\ge 0, y \ge 0$

Số công nhân là: $10x+20y$

Diện tích trồng rau và hoa là 10 hec ta nên ta có: $x+y \le 10$

Vì số công nhân không quá 160 người nên ta có: $10x+20y \le 160$

Khi đó $x,y$ phải thỏa mãn hệ: \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 10\\10x + 20y \le 160\end{array} \right.\)

Biểu diễn tập nghiệm ta được miền nghiệm là tứ giác OABC với $O(0;0),A(10;0),B(4;6),C(0;8)$:

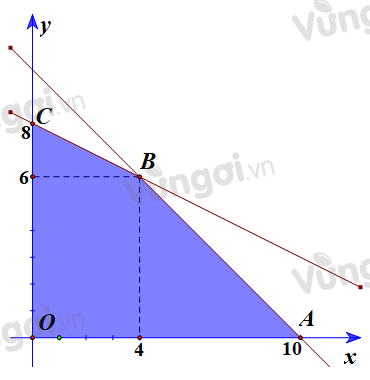
Lợi nhuận là $L=3x+4y$

$L(10;0)=30;L(4;6)=3.4+4.6=36;L(0;8)=4.8=32$

Xét giá trị của L tại các đỉnh O, A, B, C và so sánh ta suy ra $x=4;y=6$ là diện tích cần trồng để thu được nhiều lợi nhuận nhất $L=36$ triệu đồng.

Vậy $x=4$

+) Đáp án A: \(0 + 3.0 + 2 = 2 \ge 0 \Rightarrow \) đáp án A sai.

+) Đáp án B: \(0 + 0 + 2 = 2 \ge 0 \Rightarrow \) đáp án B sai.

+) Đáp án C: \(2.0 + 5.0 - 2 =  - 2 < 0 \Rightarrow \) đáp án C sai.

+) Đáp án D: \(2.0 + 0 + 2 = 2 \ge 0 \Rightarrow \) đáp án D đúng.

\( \Rightarrow O\left( {0;0} \right)\) là nghiệm của BPT: \(2x + y + 2 \ge 0\)

+) Đáp án A: \(\left\{ \begin{array}{l}1 + 3.1 - 2 = 2 \ge 0\\2.1 + 1 + 1 = 4 \le 0\left( {ktm} \right)\end{array} \right.\)

\( \Rightarrow \) đáp án A sai.

+) Đáp án A: \(\left\{ \begin{array}{l} - 1 + 3.2 - 2 = 3 \ge 0\\2.\left( { - 1} \right) + 2 + 1 = 1 \le 0\left( {ktm} \right)\end{array} \right.\)

\( \Rightarrow \) đáp án B sai.

+) Đáp án C: \(\left\{ \begin{array}{l} - 2 + 3.2 - 2 = 2 \ge 0\\2.\left( { - 2} \right) + 2 + 1 =  - 1 \le 0\end{array} \right.\)

\( \Rightarrow \) đáp án C đúng.

\( \Rightarrow \) Điểm \(\left( { - 2;2} \right)\) là nghiệm của hệ BPT đề bài 

- Theo định nghĩa thì \(x + y \ge 0\)là bất phương trình bậc nhất hai ẩn.

- Các bất phương trình còn lại là bất phương trình bậc hai.

+) Đáp án A: ta có: \( - 2.\left( { - 3} \right) + 1 + 1 = 8 < 0\) vô lý \( \Rightarrow \) loại đáp án A.

+) Đáp án B: Ta có: \( - 3 + 1 + 2 = 0 > 0\) vô lý \( \Rightarrow \) loại đáp án B.

+) Đáp án C: Ta có: \( - 3 + 2.1 + 2 = 1 > 0\) \( \Rightarrow \) chọn đáp án C.

Vậy cặp số \(\left( { - 3;1} \right)\) là nghiệm của BPT \(x + 2y + 2 > 0\)

Thay tọa độ điểm \(M\left( {1;\;1} \right)\) vào hệ BPT ta có: \(\left\{ \begin{array}{l}2.1 - 1 + 2 = 3 \ge 0\\ - 1 - 2.1 - 2 =  - 5 < 0\end{array} \right.\)

Vậy điểm \(M\left( {1;1} \right)\) thuộc miền nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x - y + 2 \ge 0\\ - x - 2y - 2 < 0\end{array} \right..\)

Ta có \(3x + 2\left( {y + 3} \right) > 4\left( {x + 1} \right) - y + 3\, \Leftrightarrow \, - x + 3y - 1 > 0\).

Vì \( - 3 + 3.2 - 1 > 0\) là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ (3;2).

Ta có \(3\left( {x - 1} \right) + 4\left( {{\rm{ }}y - 2} \right) < 5x - 3\, \Leftrightarrow \, - 2x + 4y - 8 < 0\).

Vì \( - 2.0 + 4.0 - 8 < 0\) là mệnh đề đúng nên miền nghiệm của bất phương trình trên chứa điểm có tọa độ \(\left( {0;0} \right)\).

Vì \( - 3.\left( { - 1} \right) + 2.3 - 4 > 0\) là mệnh đề đúng nên \(A\left( { - 1;3} \right)\) là điểm thuộc miền nghiệm của bất phương trình \( - 3x + 2y - 4 > 0\).

Vì \(2 - 3 < 0\) là mệnh đề đúng nên cặp số $\left( {2;3} \right)$ là nghiệm của bất phương trình $x-y < 0$.

Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

Với \(M\left( {0;1} \right) \Rightarrow \)\(\left\{ \begin{array}{l}0 + 3.1 - 2 \ge 0\\2.0 + 1 + 1 \le 0\end{array} \right.\). Bất phương trình thứ hai sai nên A sai.

Với \(N\left( {-1;1} \right) \Rightarrow \)\(\left\{ \begin{array}{l} - 1 + 3.1 - 2 \ge 0\\2.\left( { - 1} \right) + 1 + 1 \le 0\end{array} \right.\): Đúng.

Ta thay lần lượt tọa độ các điểm vào hệ bất phương trình.

Với \(O\left( {0;0} \right) \Rightarrow \)\(\left\{ \begin{array}{l}2.0 - 5.0 - 1 > 0\\2.0 + 0 + 5 > 0\\0 + 0 + 1 < 0\end{array} \right.\). Bất đẳng thức thứ nhất và thứ ba sai nên A sai.

Với \(M\left( {1;0} \right) \Rightarrow \)\(\left\{ \begin{array}{l}2.1 - 5.0 - 1 > 0\\2.1 + 0 + 5 > 0\\1 + 0 + 1 < 0\end{array} \right.\). Bất đẳng thức thứ ba sai nên B sai.

Với \(N\left( {0; - 2} \right) \Rightarrow \)\(\left\{ \begin{array}{l}2.0 - 5.\left( { - 2} \right) - 1 > 0\\2.0 + \left( { - 2} \right) + 5 > 0\\0 + \left( { - 2} \right) + 1 < 0\end{array} \right.\): Đúng.

Với \(P(0;2)\) ta có: $\left\{ \begin{array}{l}
2.0 - 5.2 - 1 > 0\\
2.0 + 2 + 5 > 0\\
0 + 2 + 1 < 0
\end{array} \right.$

Bất đẳng thức thứ nhất và thứ ba sai nên P không thuộc miền nghiệm.

Vậy chỉ có điểm N thỏa mãn.