Trên đường tròn tùy ý, cung có số đo $1\,rad$ là:
Cung có số đo $1\,rad$ có độ dài: \(l = \alpha .R = 1.R = R\).
Kết quả nào sau đây đúng ?
Ta có: $\pi \,rad = {180^0}$
Trên đường tròn có bán kính $r = 5$, độ dài của cung có số đo $\dfrac{\pi }{8}$ là:
$l = R\alpha = 5.\dfrac{\pi }{8} = \dfrac{{5\pi }}{8}$.
Trên đường tròn lượng giác, khẳng định nào sau đây là đúng?
Đáp án A sai vì cung lượng giác có điểm đầu \(A\) điểm cuối \(B\) có vô số số đo hơn kém nhau \(k2\pi \).
Đáp án B sai vì chẳng hạn cung lượng giác \(AB\) có số đo \(\dfrac{\pi }{3}\) sẽ có các cặp số đo: \(\dfrac{\pi }{3};\dfrac{{5\pi }}{3}\) hay \(\dfrac{\pi }{3} + 6\pi ;\dfrac{{5\pi }}{3} - 6\pi \) hay nhũng cặp số đo khác mà tổng của chúng đều bằng \(2\pi \) chứ không phải chỉ \(1\).
Đáp án C sai vì cung lượng giác có điểm đầu \(A\) điểm cuối \(B\) có vô số số đo hơn kém nhau \(2\pi \).
Và do đó đáp án D đúng.
Giá trị của $\tan {180^0}$ bằng:
Ta có: \(\tan {180^0} = 0\)
Cung $\alpha $ có điểm đầu là $A,$ điểm cuối trùng với một trong bốn điểm $M,N,P,Q$
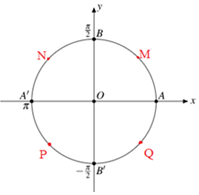
Số đo của cung $\alpha $ là:
Khi điểm cuối là $M$ ta có: \(\alpha = \dfrac{\pi }{4} + k2\pi \,\,\left( {k \in Z} \right)\)
Khi điểm cuối là $N$ thì \(\alpha = \dfrac{{3\pi }}{4} + k2\pi \,\,\left( {k \in Z} \right)\)
Khi diểm cuối là $P$ thì \(\alpha = \dfrac{{5\pi }}{4} + k2\pi \,\,\left( {k \in Z} \right)\)
Khi điểm cuối là $Q$ thì \(\alpha = \dfrac{{7\pi }}{4} + k2\pi \,\,\left( {k \in Z} \right)\)
\( \Rightarrow \alpha = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}\,\,\left( {k \in Z} \right)\)
Giá trị của $\cot \dfrac{{89\pi }}{6}$ bằng:
Ta có: $\cot \dfrac{{89\pi }}{6} = \cot \left( {15\pi - \dfrac{\pi }{6}} \right) = \cot \left( { - \dfrac{\pi }{6}} \right) = - \sqrt 3 $
Góc có số đo ${105^0}$ đổi sang radian là:
Ta có: ${105^0} = 105.\dfrac{\pi }{{180}}rad = \dfrac{{7\pi }}{{12}}$
Cho $\cot x = \dfrac{3}{4}$ và góc $x$ thỏa mãn ${90^0} < x < {180^0}$. Khi đó:
$\cot x = \dfrac{3}{4} \Leftrightarrow \tan \,x=\dfrac{1}{\cot x} = \dfrac{4}{3}$
=>Phương án A sai
$1 + {\cot ^2}x = \dfrac{1}{{{{\sin }^2}x}}$ $ \Leftrightarrow 1 + {\left( {\dfrac{3}{4}} \right)^2} = \dfrac{1}{{{{\sin }^2}x}}$ $ \Leftrightarrow {\sin ^2}x = \dfrac{{16}}{{25}} $ $\Leftrightarrow \sin \,x = \pm \dfrac{4}{5}$.
Mà ${90^0} < x < {180^0} \Rightarrow \sin \,x >0\Rightarrow \sin \,x = \dfrac{4}{5}$
=> Phương án D sai, C đúng.
Vì ${\sin ^2}x = \dfrac{{16}}{{25}} \Rightarrow {\cos ^2}x=1-{\sin ^2}x = \dfrac{9}{{25}}$ $ \Leftrightarrow \cos x= \pm \dfrac{3}{5}$
Mà ${90^0} < x < {180^0} \Rightarrow \cos x <0\Rightarrow \cos x = - \dfrac{3}{5}$
=>Phương án B sai.
Biểu thức $\cos \left( { - \dfrac{{23\pi }}{6}} \right) - \dfrac{1}{{{{\cos }^2}\dfrac{{16\pi }}{3}}} + \cot \dfrac{{23\pi }}{6} = ?$
$\cos \left( { - \dfrac{{23\pi }}{6}} \right) - \dfrac{1}{{{{\cos }^2}\dfrac{{16\pi }}{3}}} + \cot \dfrac{{23\pi }}{6}$
$ = \cos \left( { - 4\pi + \dfrac{\pi }{6}} \right) - \dfrac{1}{{\dfrac{{1 + \cos \dfrac{{32\pi }}{3}}}{2}}} + \cot \left( {4\pi - \dfrac{\pi }{6}} \right)$
$ = \cos \dfrac{\pi }{6} - \dfrac{2}{{1 + \cos \left( {10\pi + \dfrac{{2\pi }}{3}} \right)}} + \cot \left( { - \dfrac{\pi }{6}} \right)$
$ = \cos \dfrac{\pi }{6} - \dfrac{2}{{1 + \cos \dfrac{{2\pi }}{3}}} - \cot \dfrac{\pi }{6}$
$ = \dfrac{{\sqrt 3 }}{2} - \dfrac{2}{{1 - \dfrac{1}{2}}} - \sqrt 3 = - \dfrac{{\sqrt 3 }}{2} - 4$
Cho $A,B,C$ là $3$ góc của một tam giác. Hãy xác định hệ thức sai:
$ \sin \left ( {B + C} \right) = \sin (\pi - A) = \sin A $
$\sin \dfrac{{A + B}}{2} = \sin \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right) = \cos \dfrac{C}{2}$
$\cos (3A + B + C) = \cos (2A + \pi ) = - \cos 2A$
$\sin \dfrac{{B + C}}{2} = \sin \left( {\dfrac{\pi }{2} - \dfrac{A}{2}} \right) = \cos \dfrac{A}{2}$
Hãy xác định kết quả sai:
$\sin \dfrac{{7\pi }}{{12}} = \sin \left( {\dfrac{\pi }{3} + \dfrac{\pi }{4}} \right)$$ = \sin \dfrac{\pi }{3}\cos \dfrac{\pi }{4} + \sin \dfrac{\pi }{4}\cos \dfrac{\pi }{3}$$ = \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 2 }}{2} + \dfrac{1}{2}.\dfrac{{\sqrt 2 }}{2} = \dfrac{{\sqrt 6 + \sqrt 2 }}{4}$
$\cos {285^0} = \cos \left( {{{360}^0} - {{75}^0}} \right)$$ = \cos {75^0} = \cos \left( {{{30}^0} + {{45}^0}} \right)$$ = \cos {30^0}\cos {45^0} - \sin {30^0}\sin {45^0}$$ = \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 2 }}{2} - \dfrac{1}{2}.\dfrac{{\sqrt 2 }}{2}$$ = \dfrac{{\sqrt 6 - \sqrt 2 }}{4}$
$\sin \dfrac{\pi }{{12}} = \sin \left( {\dfrac{\pi }{3} - \dfrac{\pi }{4}} \right)$$ = \sin \dfrac{\pi }{3}\cos \dfrac{\pi }{4} - \cos \dfrac{\pi }{3}\sin \dfrac{\pi }{4}$$ = \dfrac{{\sqrt 3 }}{2}.\dfrac{{\sqrt 2 }}{2} - \dfrac{1}{2}.\dfrac{{\sqrt 2 }}{2}$$ = \dfrac{{\sqrt 6 - \sqrt 2 }}{4}$
$\sin \dfrac{{103\pi }}{{12}} = \sin \left( {8\pi + \dfrac{{7\pi }}{{12}}} \right)$$ = \sin \dfrac{{7\pi }}{{12}} = \dfrac{{\sqrt 6 + \sqrt 2 }}{4}$
Xét tính chất của tam giác $ABC$ biết rằng: $\cos A + \cos B - \cos C + 1 = \sin A + \sin B + \sin C$
Ta có:
$\cos A + \cos B - \cos C + 1$ $ = 2\cos \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2} + 2{\sin ^2}\dfrac{C}{2}$$ = 2\cos \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right)\cos \dfrac{{A - B}}{2} + 2{\sin ^2}\dfrac{C}{2}$ $ = 2\sin \dfrac{C}{2}\cos \dfrac{{A - B}}{2} + 2{\sin ^2}\dfrac{C}{2}$$ = 2\sin \dfrac{C}{2}\left( {\cos \dfrac{{A - B}}{2} + \sin \dfrac{C}{2}} \right)$ $ = 2\sin \dfrac{C}{2}\left( {\cos \dfrac{{A - B}}{2} + \cos \dfrac{{A + B}}{2}} \right)$ $ = 2\sin \dfrac{C}{2}.2\cos \dfrac{A}{2}.\cos \dfrac{B}{2}$ $ = 4\cos \dfrac{A}{2}\cos \dfrac{B}{2}\sin \dfrac{C}{2}$
$\sin A + \sin B + \sin C$ $ = 2\sin \dfrac{{A + B}}{2}\cos \dfrac{{A - B}}{2} + 2\sin \dfrac{C}{2}\cos \dfrac{C}{2}$ $ = 2\sin \left( {\dfrac{\pi }{2} - \dfrac{C}{2}} \right)\cos \dfrac{{A - B}}{2} + 2\sin \dfrac{C}{2}\cos \dfrac{C}{2}$ $ = 2\cos \dfrac{C}{2}\cos \dfrac{{A - B}}{2} + 2\sin \dfrac{C}{2}\cos \dfrac{C}{2}$ $ = 2\cos \dfrac{C}{2}\left( {\cos \dfrac{{A - B}}{2} + \sin \left( {\dfrac{\pi }{2} - \dfrac{{A + B}}{2}} \right)} \right)$ $ = 2\cos \dfrac{C}{2}\left( {\cos \dfrac{{A - B}}{2} + \cos \dfrac{{A + B}}{2}} \right)$
$ = 2\cos \dfrac{C}{2}.2\cos \dfrac{A}{2}\cos \dfrac{B}{2}$ $ = 4\cos \dfrac{A}{2}\cos \dfrac{B}{2}\cos \dfrac{C}{2}$
$\dfrac{{\cos A + \cos B - \cos C + 1}}{{\sin A + \sin B + \sin C}}$ $ = \dfrac{{4\cos \dfrac{A}{2}\cos \dfrac{B}{2}\sin \dfrac{C}{2}}}{{4\cos \dfrac{A}{2}\cos \dfrac{B}{2}\cos \dfrac{C}{2}}} = \tan \dfrac{C}{2}$
$ \Rightarrow \tan \dfrac{C}{2} = 1 \Leftrightarrow \dfrac{C}{2} = {45^0} \Leftrightarrow C = {90^0}$
$ \Rightarrow \Delta ABC$ vuông tại $C.$
Hãy xác định hệ thức sai:
$\sin \,x{\cos ^3}x - \cos x{\sin ^3}x$ $ = \sin \,x.\dfrac{{3\cos x + \cos 3x}}{4} - \cos x.\dfrac{{3\sin \,x - \sin 3x}}{4}$
$ = \dfrac{3}{4}\sin \,x\cos x + \dfrac{1}{4}\sin \,x\cos 3x$ $ - \dfrac{3}{4}\sin \,x\cos \,x + \dfrac{1}{4}\sin 3x\cos x$
$ = \dfrac{1}{4}\left( {\sin \,x\cos 3x + \sin 3x\cos x} \right)$ $ = \dfrac{1}{4}\sin (x + 3x) = \dfrac{{\sin 4x}}{4}$
${\sin ^4}x + {\cos ^4}x$ $ = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x$ $ = 1 - \dfrac{1}{2}{\sin ^2}2x$ $ = 1 - \dfrac{1}{2}.\dfrac{{1 - \cos 4x}}{2} = \dfrac{{3 + \cos 4x}}{4}$
${\cot ^2}x + {\tan ^2}x$ $ = \dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}} + \dfrac{{{{\sin }^2}x}}{{{{\cos }^2}x}}$ $ = \dfrac{{{{\cos }^4}x + {{\sin }^4}x}}{{{{\sin }^2}x{{\cos }^2}x}}$ $ = \dfrac{{\dfrac{{3 + \cos 4x}}{4}}}{{\dfrac{1}{4}{{\sin }^2}2x}}$ $ = \dfrac{{3 + \cos 4x}}{{\dfrac{1}{2}(1 - \cos 4x)}}$ $ = \dfrac{{2\cos 4x + 6}}{{1 - \cos 4x}}$
Nếu $\sin x = \dfrac{4}{5}$ thì giá trị của $\cos 4x = ?$
$\cos 4x = 2{\cos ^2}2x - 1$ $ = 2.{\left( {1 - 2{{\sin }^2}x} \right)^2} - 1$ $ = 2{\left( {1 - 2.{{\left( {\dfrac{4}{5}} \right)}^2}} \right)^2} - 1$ $ = - \dfrac{{527}}{{625}}$
Nếu $\sin a - \cos a = \dfrac{1}{5}\,\,\left( {{{135}^0} < a < {{180}^0}} \right)$ thì giá trị đúng của $\tan 2a$ là:
$\sin a - \cos a = \dfrac{1}{5}\, \Rightarrow {\left( {\sin a - \cos a} \right)^2} = \dfrac{1}{{25}} \Leftrightarrow {\sin ^2}a - 2\sin a\cos a + {\cos ^2}a = \dfrac{1}{{25}} \Leftrightarrow 1 - \sin 2a = \dfrac{1}{{25}} \Leftrightarrow \sin 2a = \dfrac{{24}}{{25}}$
Ta có: ${\sin ^2}2a + {\cos ^2}2a = 1 \Rightarrow {\left( {\dfrac{{24}}{{25}}} \right)^2} + {\cos ^2}2a = 1 \Leftrightarrow {\cos ^2}2a = \dfrac{{49}}{{625}} \Leftrightarrow \cos 2a = \pm \dfrac{7}{{25}}$
Mà ${135^0} < a < {180^0} \Leftrightarrow {270^0} < 2a < {360^0} \Rightarrow \cos 2a > 0 \Rightarrow \cos 2a = \dfrac{7}{{25}}$
$\tan 2a = \dfrac{{\sin 2a}}{{\cos 2a}} = \dfrac{{\dfrac{{24}}{{25}}}}{{\dfrac{7}{{25}}}} = \dfrac{{24}}{7}$
Biểu thức $\dfrac{{2{{\cos }^2}x - 1}}{{4\tan \left( {\dfrac{\pi }{4} - x} \right){{\sin }^2}\left( {\dfrac{\pi }{4} + x} \right)}}$ có kết quả rút gọn bằng:
$\dfrac{{2{{\cos }^2}x - 1}}{{4\tan \left( {\dfrac{\pi }{4} - x} \right){{\sin }^2}\left( {\dfrac{\pi }{4} + x} \right)}}$ $ = \dfrac{{\cos 2x}}{{4.\dfrac{{\sin \left( {\dfrac{\pi }{4} - x} \right)}}{{\cos \left( {\dfrac{\pi }{4} - x} \right)}}.\dfrac{{1 - \cos \left( {\dfrac{\pi }{2} + 2x} \right)}}{2}}}$ $ = \dfrac{{\cos 2x}}{{2.\dfrac{{\sqrt 2 \left( {\cos x - \sin \,x} \right)}}{{\sqrt 2 \left( {\cos x + \sin \,x} \right)}}.\left( {1 + \sin 2x} \right)}}$
$ = \dfrac{{\cos 2x}}{{2.\dfrac{{\left( {\cos x - \sin \,x} \right)}}{{\left( {\cos x + \sin \,x} \right)}}.{{\left( {\sin \,x + \cos x} \right)}^2}}}$ $ = \dfrac{{\cos 2x}}{{2\left( {\cos x - \sin \,x} \right)\left( {\sin \,x + \cos x} \right)}}$ $ = \dfrac{{\cos 2x}}{{2\left( {{{\cos }^2}x - {{\sin }^2}x} \right)}}$ $ = \dfrac{{\cos 2x}}{{2\cos 2x}} = \dfrac{1}{2}$
Cho $\sin a = \dfrac{3}{5}$ và ${90^0} < a < {180^0}$. Tính $A = \dfrac{{\cot a - 2\tan a}}{{\tan \,a + 3\cot a}}$.
$A = \dfrac{{\cot a - 2\tan a}}{{\tan \,a + 3\cot a}} = \dfrac{{\cot \,a - \dfrac{2}{{\cot a}}}}{{\dfrac{1}{{\cot a}} + 3\cot a}} = \dfrac{{{{\cot }^2}a - 2}}{{1 + 3{{\cot }^2}a}}$
Mà: ${\cot ^2}a + 1 = \dfrac{1}{{{{\sin }^2}a}} \Leftrightarrow {\cot ^2}a + 1 = \dfrac{1}{{{{\left( {\dfrac{3}{5}} \right)}^2}}} \Leftrightarrow {\cot ^2}a = \dfrac{{16}}{9}$
$ \Rightarrow A = \dfrac{{\dfrac{{16}}{9} - 2}}{{1 + 3.\dfrac{{16}}{9}}} = - \dfrac{2}{{57}}$
Cho biểu thức $A = 2{\sin ^6}x + 2{\cos ^6}x - {\sin ^4}x - {\cos ^4}x + \cos 2x$ có giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M, m. Khi đó, $M + m = ? $
$A = 2{\sin ^6}x + 2{\cos ^6}x$ $ - {\sin ^4}x - {\cos ^4}x + \cos 2x$ $ = 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)$ $ - \left( {{{\sin }^4}x + {{\cos }^4}x} \right) + \cos 2x$
$ = 2\left( {\dfrac{1}{4} + \dfrac{3}{4}{{\cos }^2}2x} \right)$$ - \left( {\dfrac{1}{2} + \dfrac{1}{2}{{\cos }^2}2x} \right) + \cos 2x$ $ = {\cos ^2}2x + \cos 2x$
Đặt $\cos 2x = t,\,\,t \in \left[ { - 1;1} \right]$
Khi đó, $A = {t^2} + t,\,\,t \in \left[ { - 1;1} \right]$. Ta có:
$A = {t^2} + t = {\left( {t + \dfrac{1}{2}} \right)^2} - \dfrac{1}{4} \ge - \dfrac{1}{4}$ $ \Rightarrow \mathop {\min }\limits_{t \in \left[ { - 1;1} \right]} A = - \dfrac{1}{4}$ khi và chỉ khi $t = - \dfrac{1}{2} \Rightarrow m = - \dfrac{1}{4}$.
$A = {t^2} + t$ $ = {t^2} - t + 2t - 2 + 2$$ = t(t - 1) + 2(t - 1) + 2$
$ = (t - 1)(t + 2) + 2 \le 2$ (vì $t \in \left[ { - 1;1} \right] \Rightarrow t - 1 \le 0,\,\,t + 2 > 0$)
$ \Rightarrow \mathop {\max }\limits_{t \in \left [ { - 1;1} \right]} A = 2$ khi và chỉ khi $ t = 1 \Rightarrow M = 2$
Vậy, $M + m = 2 + \dfrac{{ - 1}}{4} = \dfrac{7}{4}$.
Rút gọn biểu thức $B = {\sin ^3}\dfrac{a}{3} + 3{\sin ^3}\dfrac{a}{{{3^2}}} + {3^2}{\sin ^3}\dfrac{a}{{{3^3}}} + ... + {3^{n - 1}}{\sin ^3}\dfrac{a}{{{3^n}}}$ bằng:
$B = {\sin ^3}\dfrac{a}{3} + 3{\sin ^3}\dfrac{a}{{{3^2}}} + {3^2}{\sin ^3}\dfrac{a}{{{3^3}}} + ... + {3^{n - 1}}{\sin ^3}\dfrac{a}{{{3^n}}}$
$ = \dfrac{{3\sin \dfrac{a}{3} - \sin a}}{4} + 3.\dfrac{{3\sin \dfrac{a}{{{3^2}}} - \sin \dfrac{a}{3}}}{4}$ $ + {3^2}.\dfrac{{3\sin \dfrac{a}{{{3^3}}} - \sin \dfrac{a}{{{3^2}}}}}{4} + .... + {3^{n - 1}}.\dfrac{{3\sin \dfrac{a}{{{3^n}}} - \sin \dfrac{a}{{{3^{n - 1}}}}}}{4}$
$ = \dfrac{1}{4}.\left( { - \sin a + 3\sin \dfrac{a}{3} - 3\sin \dfrac{a}{3}} \right.$ $ + {3^2}\sin \dfrac{a}{{{3^2}}} - {3^2}\sin \dfrac{a}{{{3^2}}} + {3^3}\sin \dfrac{a}{{{3^3}}}$\(\left. { - ... - {3^{n - 1}}\sin \dfrac{a}{{{3^{n - 1}}}} + {3^n}\sin \dfrac{a}{{{3^n}}}} \right)\)
$ = \dfrac{1}{4}\left( {{3^n}\sin \dfrac{a}{{{3^n}}} - \sin a} \right)$ $ = \dfrac{{{3^n}\sin \dfrac{a}{{{3^n}}} - \sin a}}{4}$

