Cho đồ thị hàm số $y = a{x^2} + bx + c\,$như hình vẽ.

Khẳng định nào sau đây là đúng:
Bề lõm của đồ thị quay xuống dưới nên hệ số $a < 0$.
Giao điểm của đồ thị hàm số với trục tung nằm trên trục có tung độ dương nên $c > 0$.
Hoành độ đỉnh $x = - \dfrac{b}{{2a}} < 0$. Mà $a < 0$ nên $b < 0$.
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 2$ biết rằng Parabol đi qua hai điểm $M\left( {1;\,\,5} \right)$ và $N\left( {2;\,\, - 2} \right)$.
Vì $M,\,\,N \in \left( P \right)$ nên tọa độ của hai điểm M, N phải thỏa mãn phương trình của $\left( P \right)$.
Do đó, ta có hệ phương trình $\left\{ \begin{array}{l}5 = a + b + 2\\ - 2 = 4a + 2b + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 5\\b = 8\end{array} \right.$.
Vậy phương trình của $\left( P \right)$là: $y = - 5{x^2} + 8x + 2$.
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx - 5$ biết rằng Parabol đi qua điểm $A\left( {3;\,\, - 4} \right)$ và có trục đối xứng $x = - \dfrac{3}{2}$.
$\left( P \right)$ đi qua điểm $A\left( {3;\,\, - 4} \right)$ nên $ - 4 = 9a + 3b - 5 \Leftrightarrow 9a + 3b = 1$.
Trục đối xứng $x = - \dfrac{b}{{2a}} = - \dfrac{3}{2} \Leftrightarrow b = 3a$.
Suy ra hệ phương trình $\left\{ \begin{array}{l}9a + 3b = 1\\3a - b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{{18}}\\b = \dfrac{1}{6}\end{array} \right.$.
Vậy phương trình của $\left( P \right)$là: $y = \dfrac{1}{{18}}{x^2} + \dfrac{1}{6}x - 5$.
Xác định Parabol $\left( P \right):\,\,y = a{x^2} + bx + 3$ biết rằng Parabol có đỉnh $I\left( {3;\,\, - 2} \right)$.
Ta có đỉnh của $\left( P \right)$có tọa độ $\left\{ \begin{array}{l}x = - \dfrac{b}{{2a}} = 3\\y = 9a + 3b + 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6a + b = 0\\9a + 3b = - 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{5}{9}\\b = - \dfrac{{10}}{3}\end{array} \right.$.
Suy ra phương trình của Parabol $\left( P \right)$là: $y = \dfrac{5}{9}{x^2} - \dfrac{{10}}{3}x + 3$.
Viết phương trình của Parabol $(P)$ biết rằng $(P)$ đi qua các điểm $A\left( {0;\,\,2} \right),\,\,B\left( { - 2;\,\,5} \right),\,\,C\left( {3;\,\,8} \right)$
Phương trình $\left( P \right)$ có dạng $y = a{x^2} + bx + c\,\,\,\,\left( {a \ne 0} \right)$
Ba điểm $A,\,\,B,\,\,C$ thuộc $\left( P \right)$ nên tọa độ của chúng phải thỏa mãn phương trình $\left( P \right)$
Do đó, ta có hệ phương trình:$\left\{ \begin{array}{l}2 = a{.0^2} + b.0 + c\\5 = a.{\left( { - 2} \right)^2} + b.\left( { - 2} \right) + c\\8 = a{.3^2} + b.3 + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{7}{{10}}\\b = - \dfrac{1}{{10}}\\c = 2\end{array} \right.$
Suy ra phương trình của $\left( P \right)$ là: $y = \dfrac{7}{{10}}{x^2} - \dfrac{1}{{10}}x + 2$
Cho hàm số \(y = a{x^2} + bx + c\) đạt giá trị nhỏ nhất bằng 4 tại \(x = - 2\) và đồ thị đi qua \(A\left( {0;6} \right)\). Tính tích \(abc?\)
Hàm số \(y = a{x^2} + bx + c\) đạt giá trị nhỏ nhất bằng 4 tại \(x = - 2\) nên \(a > 0\) và có đỉnh \(I\left( { - 2;\,\,4} \right)\)
\( \Rightarrow \left\{ \begin{array}{l}\dfrac{{ - b}}{{2a}} = - 2\\f\left( { - 2} \right) = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\4a - 2b + c = 4\end{array} \right.\,\,\,\left( 1 \right)\)
Đồ thị đi qua \(A\left( {0;6} \right)\) nên ta có \(f\left( 0 \right) = 6 \Leftrightarrow c = 6\)
\( \Rightarrow \left( 1 \right) \Leftrightarrow \left\{ \begin{array}{l}4a - b = 0\\4a - 2b + 6 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\,\,\,\left( {tm} \right)\\b = 2\end{array} \right.\)
Vậy tích \(abc = \dfrac{1}{2}.2.6 = 6\)
Parabol \(\left( P \right):y = a{x^2} + bx + c\) qua ba điểm \(A\left( {1;1} \right),B\left( {2; - 3} \right),C\left( {5; - 2} \right)\). Tính \(30a + 8b + 3c\).
Parabol \(\left( P \right):y = a{x^2} + bx + c\) qua ba điểm \(A\left( {1;1} \right),B\left( {2; - 3} \right),C\left( {5; - 2} \right)\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}a + b + c = 1\\4a + 2b + c = - 3\\25a + 5b + c = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{13}}{{12}}\\b = \dfrac{{ - 29}}{4}\\c = \dfrac{{43}}{6}\end{array} \right.\)\( \Rightarrow 30a + 8b + 3c = - 4\)
Cho đồ thị hàm số \(y = {x^2} - 2x - 1\left( P \right).\)Dựa vào đồ thị \(\left( P \right)\) xác định số giá trị nguyên dương của \(m\) để phương trình \({x^2} - 2x + 2m - 2 = 0\) có nghiệm \(x \in \left[ { - 1;2} \right]?\)
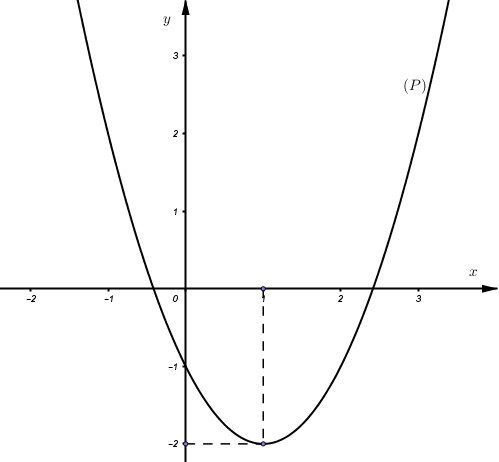
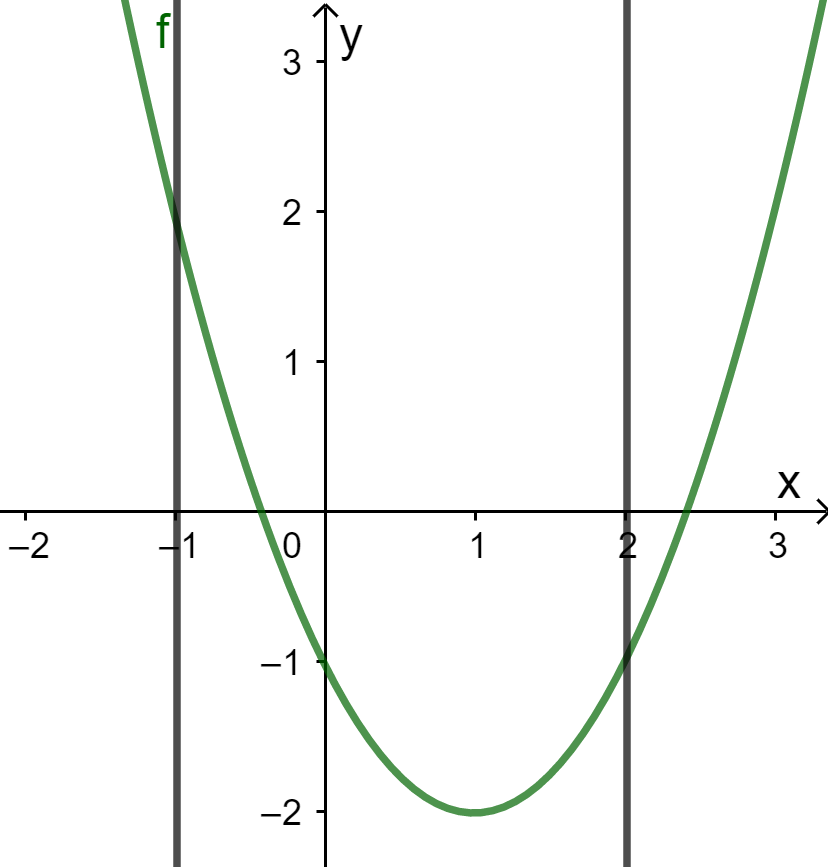
\({x^2} - 2x + 2m - 2 = 0\)\( \Leftrightarrow {x^2} - 2x - 1 = 1 - 2m\)
Đây là phương trình hoành độ giao điểm của đồ thị hàm số \(\left( P \right)\) và đường thẳng \(y = 1 - 2m\) song song \(Ox\)
Xét trong đoạn \(x \in \left[ { - 1;2} \right] \Rightarrow \)\(y \in \left[ { - 2;2} \right]\)
Suy ra để phương trình có nghiệm thì \( - 2 \le 1 - 2m \le 2\)\( \Leftrightarrow \dfrac{{ - 1}}{2} \le m \le \dfrac{3}{2}\) mà \(m \in {\mathbb{Z}^ + } \Rightarrow m = 1\)
Vậy để phương trình \({x^2} - 2x + 2m - 2 = 0\) có nghiệm thì \(m = 1\).
Tìm tất cả các giá trị của \(m\) để hai đồ thị hàm số \(y = - {x^2} - 2x + 3\) và \(y = {x^2} - m\) có điểm chung ?
Xét phương trình hoành độ giao điểm của 2 đồ thị hàm số:
\(\begin{array}{l} - {x^2} - 2x + 3 = {x^2} - m\\ \Leftrightarrow 2{x^2} + 2x - m - 3 = 0\\\Delta ' = 1 + 2m + 6 = 7 + 2m\end{array}\)
Để 2 đồ thị có điểm chung thì phương trình phải có nghiệm
\( \Rightarrow \Delta \ge 0 \Leftrightarrow \) \(2m + 7 \ge 0 \Leftrightarrow \)\(m \ge \dfrac{{ - 7}}{2}\)
Họ đồ thị hàm số \(y = \left( {2 - m} \right){x^2} - \left( {m - 3} \right)x + 2m - 1\) luôn đi qua bao nhiêu điểm cố định?
Ta có
\(y = \left( {2 - m} \right){x^2} - \left( {m - 3} \right)x + 2m - 1\)
\( \Leftrightarrow y = 2{x^2} - m{x^2} - mx + 3x + 2m - 1\)
\( \Leftrightarrow \left( {m{x^2} + mx - 2} \right) + y - 2{x^2} - 3x + 1 = 0\)
\( \Leftrightarrow m\left( {{x^2} + x - 2} \right) + \left( {y - 2{x^2} - 3x + 1} \right) = 0\)
Điểm \(M\left( {x;y} \right)\) là điểm cố định của họ đồ thị hàm số đã cho khi và chỉ khi tọa độ của \(M\) thỏa mãn hệ:
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x^2} + x - 2 = 0\\y = 2{x^2} + 3x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\\y = 2{x^2} + 3x - 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1\\y = 4\end{array} \right.\\\left\{ \begin{array}{l}x = - 2\\y = 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}M\left( {1;4} \right)\\M\left( { - 2;1} \right)\end{array} \right.\end{array}\)
Vậy có 2 điểm cố định \({M_1}\left( {1;4} \right)\) và \({M_2}\left( { - 2;1} \right)\).
Cho Parabol \(\left( P \right)\) của hàm số \(y = a{x^2} + bx + c\). Tìm \(a,b,c\) biết đồ thị có đỉnh \(A\left( {\dfrac{1}{4}; - \dfrac{1}{8}} \right)\) và đi qua gốc tọa độ.
Do đồ thị có đỉnh \(A\left( {\dfrac{1}{4}; - \dfrac{1}{8}} \right)\) nên \(\left\{ \begin{array}{l} - \dfrac{b}{{2a}} = \dfrac{1}{4} \Leftrightarrow a = - 2b\\ - \dfrac{1}{8} = \dfrac{a}{{16}} + \dfrac{b}{4} + c\end{array} \right.(1)\)
Parabol đi qua gốc tọa độ nên điểm \(O\left( {0;0} \right)\) thỏa mãn hàm số, hay
\(a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\). Thay \(c = 0\) vào (1) ta được:
\(\left\{ \begin{array}{l}a = - 2b\\\dfrac{a}{{16}} + \dfrac{b}{4} = - \dfrac{1}{8}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2b\\b = -1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = -1\end{array} \right.\)
Vậy \(a = 2,b =- 1,c = 0\).
Cho Parabol \((P):y = - {x^2} + 3\). Tìm \(m\) để đường thẳng \(y = - m \) cắt \(\left( P \right)\) tại 2 điểm phân biệt
Hoành độ giao điểm của \((P)\) và \(y = - m\) là nghiệm của phương trình \( - {x^2} + 3 = - m \Leftrightarrow {x^2} = m + 3(*)\)
Đường thẳng \(y = - m\) cắt \(\left( P \right)\) tại 2 điểm phân biệt khi và chỉ khi (*) có 2 nghiệm phân biệt \( \Leftrightarrow 3 + m > 0 \Leftrightarrow m > - 3\)
Đồ thị của họ hàm số \((P):y = \left( {m - 2} \right){x^2} - x - m + 3\) có bao nhiêu điểm cố định?
Điểm $A\left( {{x_0};\,\,{y_0}} \right)$ là điểm cố định của họ $\left( {{P}} \right)$ khi và chỉ khi
$\begin{array}{l}{y_0} = (m-2)x_0^2 - {x_0} - m+3 \Leftrightarrow 2x_0^2 + {x_0} + {y_0} -3- m\left( {{x_0^2} -1} \right) = 0,\,\,\,\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}2x_0^2 + {x_0} + {y_0} = 3\\{x_0^2} - 1 = 0\end{array} \right. \end{array}$
\( \Leftrightarrow \left\{ \begin{array}{l}2{x_0}^2 + {x_0} + {y_0} = 3\\\left[ \begin{array}{l}{x_0} = 1\\{x_0} = - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x_0} = 1\\{y_0} = 0\end{array} \right.\\\left\{ \begin{array}{l}{x_0} = - 1\\{y_0} = 2\end{array} \right.\end{array} \right.\)
Suy ra $A\left( {1;\,\,0} \right)$ hoặc $A\left( {-1;\,\,2} \right)$
Vậy đồ thị luôn đi qua 2 điểm cố định.
Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại hai điểm phân biệt A, B thỏa mãn OA = 4OB. Tổng các phần tử của S bằng:
Xét phương trình hoành độ giao điểm \({x^2} + 5x + 2m = 0\) (*).
Để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại 2 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta = 25 - 8m > 0\) \( \Leftrightarrow m < \dfrac{{25}}{8}\).
Gọi \({x_1};{x_2}\) là hai nghiệm phân biệt của phương trình (*) \( \Rightarrow A\left( {{x_1};0} \right)\) và \(B\left( {{x_2};0} \right)\).
Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - 5\\{x_1}{x_2} = 2m\end{array} \right.\) (**).
Theo bài ra ta có:
OA = 4OB
\( \Leftrightarrow 4\left| {{x_1}} \right| = \left| {{x_2}} \right| \Leftrightarrow \left[ \begin{array}{l}4{x_1} = {x_2}\\ - 4{x_1} = {x_2}\end{array} \right.\)
TH1; \(4{x_1} = {x_2}\), thay vào hệ (**) ta có:
\(\left\{ \begin{array}{l}{x_1} + 4{x_1} = 5\\{x_1}.4{x_1} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 1\\4 = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 1\\m = 2\,\,\left( {tm} \right)\end{array} \right.\).
TH1; \( - 4{x_1} = {x_2}\), thay vào hệ (**) ta có:
\(\left\{ \begin{array}{l}{x_1} - 4{x_1} = 5\\{x_1}.\left( { - 4{x_1}} \right) = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = - \dfrac{5}{3}\\ - \dfrac{{100}}{9} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = - \dfrac{5}{3}\\m = - \dfrac{{50}}{9}\,\,\left( {tm} \right)\end{array} \right.\).
\( \Rightarrow S = \left\{ {2; - \dfrac{{50}}{9}} \right\}\).
Vậy tổng các phần tử của S bằng \(2 + \left( { - \dfrac{{50}}{9}} \right) = - \dfrac{{32}}{9}\).
Xác định hàm số bậc hai \(y = a{x^2} - x + c\) biết đồ thị hàm số đi qua A(1;-2) và B(2;3).
Vì A thuộc đồ thị hàm số nên \( - 2 = a - 1 + c \Leftrightarrow a + c = - 1\).
Vì B thuộc đồ thị hàm số nên \(3 = 4a - 2 + c \Leftrightarrow 4a + c = 5\).
Ta có hệ phương trình
\(\left\{ \begin{array}{l}a + c = - 1\\4a + c = 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\c = - 3\end{array} \right.\).
Vậy \(y = 2{x^2} - x - 3\).
Đồ thị hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
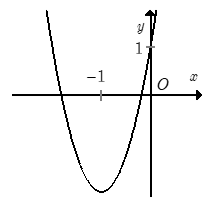
Nhận xét:
Parabol có bề lõm hướng lên. Loại đáp án A, D.
Parabol cắt trục hoành tại 2 điểm phân biệt có hoành độ âm. Xét các đáp án B và C, đáp án B thỏa mãn
Địch xây chòi phòng thủ cao \(20\;{\rm{m}}\) phía trước tường thành. Hỏi phải đặt máy bắn đá cách chòi bao xa để đạn có thể bắn trúng chòi? Biết rằng để tránh bị địch tấn công thì máy bắn đá phải đặt cách thành địch ít nhất \(50\;{\rm{m}}\).
Để máy bắn đá có thể bắn trúng chòi cao \(20\;{\rm{m}}\) thì
\( - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x = 20 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 94,35(m)}\\{x = 5,65(m)(L)}\end{array}} \right.\)
Vậy cần đặt máy bắn đá cách chòi 94,35 m để đạn có thể bắn trúng chòi.
Đồ thị hình vẽ là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
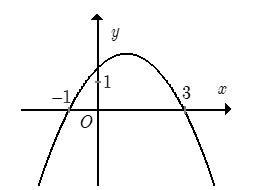
Nhận xét:
Parabol có bề lõm hướng xuống. Loại đáp án A, C.
Parabol cắt trục hoành tại 2 điểm \(\left( {3;0} \right)\) và \(\left( { - 1;0} \right)\). Xét các đáp án B và D, đáp án D thỏa mãn.
Máy bắn đá cách tường thành địch \(90\;{\rm{m}}\). Biết tường thành cao \(30\;{\rm{m}}\). Hỏi chiều cao khi đạn bay đến tường thành thì cao hơn hay thấp hơn tường thành bao nhiêu mét?
\((P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\).
Vì máy bắn đá cách tường thành địch 90 m nên \(x = 90 \Rightarrow y = 33,75(m) > 30(m)\)
\( \Rightarrow \) đạn pháo cao hơn tường thành 3,75m
Vị trí đạn bay cao nhất cách mặt đất bao nhiêu?
Bước 1: Đặt hệ trục tọa độ. Gọi \((P):y = a{x^2} + bx + c\). Tìm (P).
Đặt hệ trục như hình vẽ.
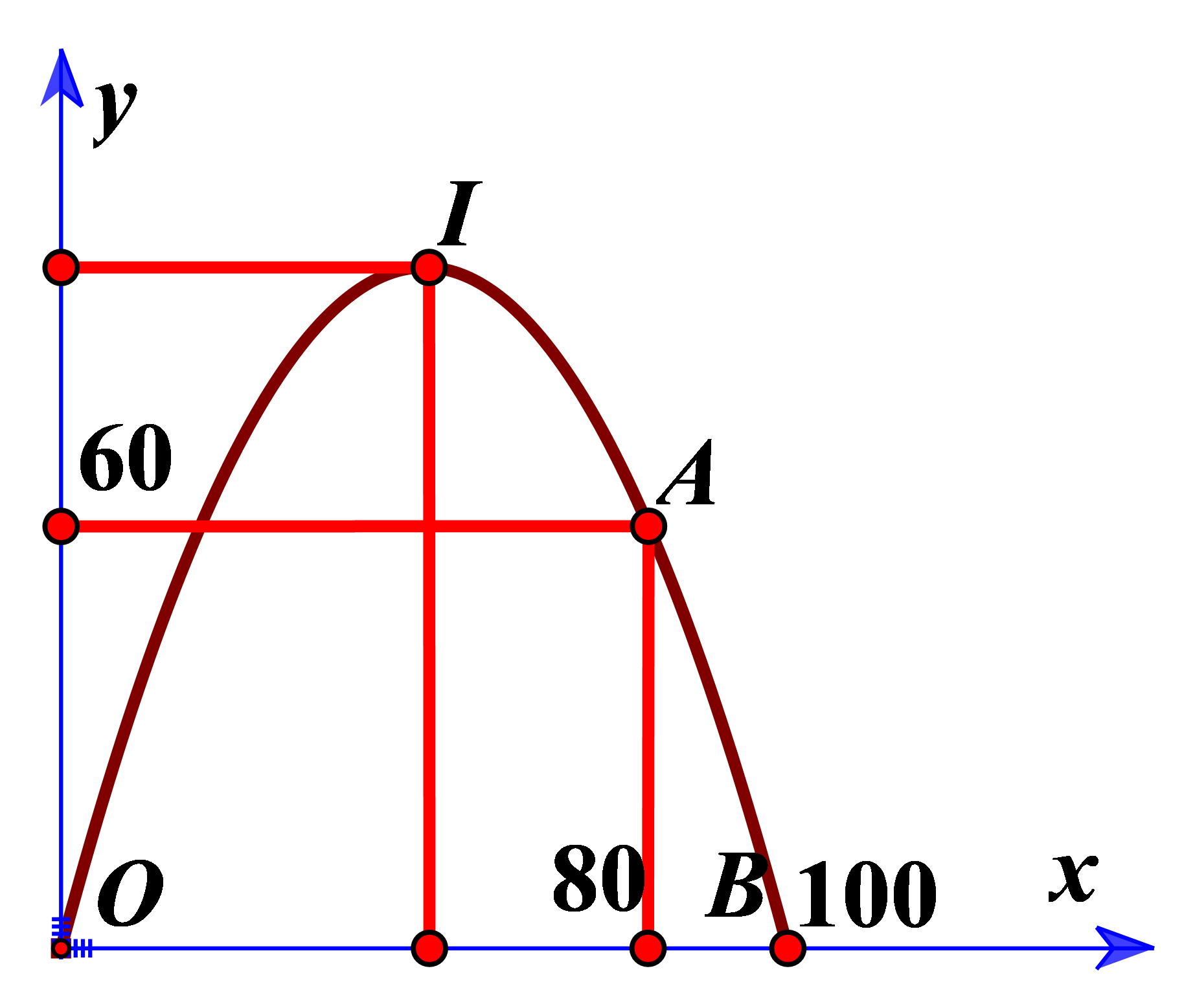
Gọi \((P):y = a{x^2} + bx + c\).
Ta có \((P)\) qua \(O(0;0),A(80;60)\) và \(B(100;0)\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{c = 0}\\{{{80}^2}a + 80b = 60}\\{{{100}^2}a + 100b = 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - \dfrac{3}{{80}}}\\{b = \dfrac{{15}}{4}}\end{array}} \right.} \right.\)
\( \Rightarrow (P):y = - \dfrac{3}{{80}}{x^2} + \dfrac{{15}}{4}x\)
Bước 2: Tìm đỉnh của (P)
Vị trí đạn bay cao nhất cách mặt đất là \({y_I} = - \dfrac{\Delta }{{4a}} = - \dfrac{{{b^2} - 4ac}}{{4a}} = \dfrac{{375}}{4} = 93,75m\).

