Tìm các giá trị của tham số $m$ để phương trình $2{x^2} - 2x + 1 - m = 0$ có hai nghiệm phân biệt
$2{x^2} - 2x + 1 - m = 0 \Leftrightarrow 2{x^2} - 2x = m - 1$
Số nghiệm của phương trình đã cho bằng số giao điểm của Parabol $\left( P \right):\,\,y = 2{x^2} - 2x$ và đường thẳng $y = m - 1$ có tính chất song song với trục hoành.
Parabol (P) có tọa độ đỉnh \(\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right) = \left( {\dfrac{1}{2}; - \dfrac{1}{2}} \right)\)
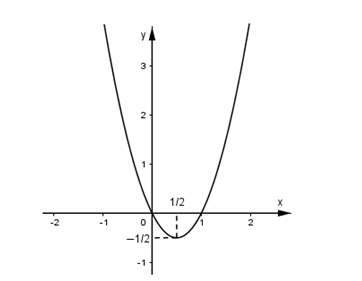
Dựa trên đồ thị ta thấy phương trình đã cho có hai nghiệm khi và chỉ khi $m - 1 > - \dfrac{1}{2} \Leftrightarrow m > \dfrac{1}{2}$
Xác định parabol \(\left( P \right):y = a{x^2} + bx + 2\), biết rằng \(\left( P \right)\) đi qua hai điểm \(M\left( {1;5} \right)\) và \(N\left( { - 2;8} \right)\).
Vì \(\left( P \right)\) đi qua hai điểm \(M\left( {1;5} \right)\) và \(N\left( { - 2;8} \right)\) nên ta có hệ
\(\left\{ \begin{array}{l}a + b + 2 = 5\\4a - 2b + 2 = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 1\end{array} \right.\). Vậy \(\left( P \right):y = 2{x^2} + x + 2\).
Xác định parabol \(\left( P \right):y = 2{x^2} + bx + c,\) biết rằng \(\left( P \right)\) đi qua điểm \(M\left( {0;4} \right)\) và có trục đối xứng \(x = 1.\)
Ta có \(M \in \left( P \right) \Rightarrow c = 4.\)
Trục đối xứng \( - \dfrac{b}{{2a}} = 1 \Rightarrow b = - 4.\)
Vậy \(\left( P \right):y = 2{x^2} - 4x + 4.\)
Tìm parabol \(\left( P \right):y = a{x^2} + 3x - 2,\) biết rằng parabol có đỉnh \(I\left( { - \dfrac{1}{2}; - \dfrac{{11}}{4}} \right).\)
Vì \(\left( P \right)\) có đỉnh \(I\left( { - \dfrac{1}{2}; - \dfrac{{11}}{4}} \right)\) nên ta có \(\left\{ \begin{array}{l} - \dfrac{b}{{2a}} = - \dfrac{1}{2}\\ - \dfrac{\Delta }{{4a}} = - \dfrac{{11}}{4}\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}b = a\\\Delta = 11a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3 = a\\9 + 8a = 11a\end{array} \right. \Leftrightarrow a = 3\).
Vậy \(\left( P \right):y = 3{x^2} + 3x - 2\).
Xác định parabol \(\left( P \right):y = a{x^2} + bx + c,\) biết rằng \(\left( P \right)\) cắt trục \(Ox\) tại hai điểm có hoành độ lần lượt là \( - 1\) và \(2\), cắt trục \(Oy\) tại điểm có tung độ bằng \( - 2\).
Gọi \(A\) và \(B\) là hai giao điểm cuả \(\left( P \right)\) với trục \(Ox\) có hoành độ lần lượt là \( - 1\) và \(2\). Suy ra \(A\left( { - 1;0} \right)\), \(B\left( {2;0} \right)\).
Gọi \(C\) là giao điểm của \(\left( P \right)\) với trục \(Oy\) có tung độ bằng \( - 2\). Suy ra \(C\left( {0; - 2} \right)\).
Theo giả thiết, \(\left( P \right)\) đi qua ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) nên ta có \(\left\{ \begin{array}{l}a - b + c = 0\\4a + 2b + c = 0\\c = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\\c = - 2\end{array} \right.\).
Vậy \(\left( P \right):y = {x^2} - x - 2\).
Tìm tất cả các giá trị thực của \(m\) để phương trình \( - 2{x^2} - 4x + 3 = m\) có nghiệm.
Xét phương trình: \( - 2{x^2} - 4x + 3 - m = 0.\) \(\left( 1 \right)\)
Để phương trình có nghiệm khi và chỉ khi \(\Delta ' \ge 0 \Leftrightarrow - 2m + 10 \ge 0 \Leftrightarrow m \le 5\).
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) đồ thị như hình. Hỏi với những giá trị nào của tham số thực \(m\) thì phương trình \(\left| {f\left( x \right)} \right| = m\) có đúng \(4\) nghiệm phân biệt.
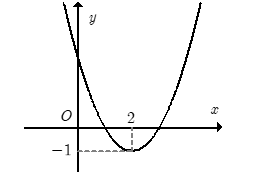
Ta có \(y = \left| {f\left( x \right)} \right| = \left\{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{;f\left( x \right) \ge 0}\\{ - f\left( x \right)}&{;f\left( x \right) < 0}\end{array}} \right.\).
Từ đó suy ra cách vẽ đồ thị hàm số \(\left( C \right)\) từ đồ thị hàm số \(y = f\left( x \right)\) như sau:
+ Giữ nguyên đồ thị \(y = f\left( x \right)\) phía trên trục hoành.
+ Lấy đối xứng phần đồ thị \(y = f\left( x \right)\) phía dưới trục hoành qua trục hoành (bỏ phần dưới).
Kết hợp hai phần ta được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như hình vẽ.
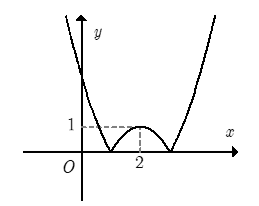
Phương trình \(\left| {f\left( x \right)} \right| = m\) là phương trình hoành độ giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đường thẳng \(y = m\) (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có yêu cầu bài toán \( \Leftrightarrow 0 < m < 1.\)
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) đồ thị như hình. Hỏi với những giá trị nào của tham số thực \(m\) thì phương trình \(f\left( {\left| x \right|} \right) - 1 = m\) có đúng \(3\) nghiệm phân biệt.
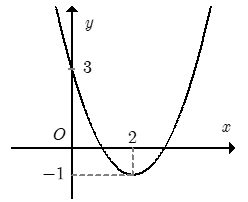
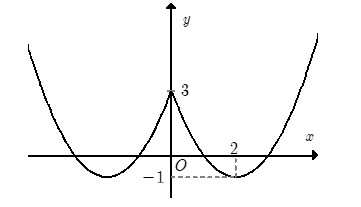
Ta có \(f\left( {\left| x \right|} \right) = f\left( x \right)\) nếu \(x \ge 0\). Hơn nữa hàm \(f\left( {\left| x \right|} \right)\) là hàm số chẵn. Từ đó suy ra cách vẽ đồ thị hàm số \(\left( C \right)\) từ đồ thị hàm số \(y = f\left( x \right)\) như sau:
+ Giữ nguyên đồ thị \(y = f\left( x \right)\) phía bên phải trục tung.
+ Lấy đối xứng phần đồ thị \(y = f\left( x \right)\) phía bên phải trục tung qua trục tung.
Kết hợp hai phần ta được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như hình vẽ.
Phương trình
\(f\left( {\left| x \right|} \right) - 1 = m \Leftrightarrow f\left( {\left| x \right|} \right) = m + 1\) là phương trình hoành độ giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = m + 1\) (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có yêu cầu bài toán \( \Leftrightarrow m + 1 = 3 \Leftrightarrow m = 2.\)
Biết rằng hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\) đạt giá trị lớn nhất bằng \(3\) tại \(x = 2\) và có đồ thị hàm số đi qua điểm \(A\left( {0; - 1} \right)\). Tính tổng \(S = a + b + c.\)
Từ giả thiết ta có hệ \(\left\{ \begin{array}{l}a < 0\\ - \dfrac{b}{{2a}} = 2\\ - \dfrac{\Delta }{{4a}} = 3\\c = - 1\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a < 0\\b = - 4a\\{b^2} - 4ac = - 12a\\c = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\b = - 4a\\16{a^2} + 16a = 0\\c = - 1\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a = 0\left( {KTM} \right)\\b = 0\\c = - 1\end{array} \right.\) hoặc \(\left\{ \begin{array}{l}a = - 1\\b = 4\\c = - 1\end{array} \right. \Rightarrow S = a + b + c = 2.\)
Biết rằng hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\) đạt giá trị lớn nhất bằng \(5\) tại \(x = - 2\) và có đồ thị đi qua điểm \(M\left( {1; - 1} \right)\). Tính tổng \(S = {a^2} + {b^2} + {c^2}.\)
Từ giả thiết, ta có hệ \(\left\{ \begin{array}{l} - \dfrac{b}{{2a}} = - 2\\4a - 2b + c = 5\\a + b + c = - 1\end{array} \right.\) \( \Leftrightarrow a = - \dfrac{2}{3};{\rm{ }}b = - \dfrac{8}{3};{\rm{ }}c = \dfrac{7}{3}\)
\( \Rightarrow S = {a^2} + {b^2} + {c^2} = 13.\)
Cho parabol \(\left( P \right):y = {x^2} - 4x + 3\) và đường thẳng \(d:y = mx + 3\). Tìm tất cả các giá trị thực của \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A,\;B\) sao cho diện tích tam giác \(OAB\) bằng \(\dfrac{9}{2}\).
Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(d\) là \({x^2} - 4x + 3 = mx + 3\)
\( \Leftrightarrow x\left[ {x - \left( {m + 4} \right)} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = m + 4\end{array} \right.\).
Để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A,\;B\) khi và chỉ khi \(4 + m \ne 0 \Leftrightarrow m \ne - 4\).
Với \(x = 0 \Rightarrow y = 3 \Rightarrow A\left( {0;3} \right) \in Oy\).
Với \(x = 4 + m \Rightarrow y = {m^2} + 4m + 3\)\( \Rightarrow B\left( {4 + m;{m^2} + 4m + 3} \right)\)
Gọi \(H\) là hình chiếu của \(B\) lên \(OA\). Suy ra \(BH = \left| {{x_B}} \right| = \left| {4 + m} \right|\).
Theo giả thiết bài toán, ta có \({S_{\Delta OAB}} = \dfrac{9}{2} \Leftrightarrow \dfrac{1}{2}OA.BH = \dfrac{9}{2}\)\( \Leftrightarrow \dfrac{1}{2}.3.\left| {m + 4} \right| = \dfrac{9}{2}\)
\( \Leftrightarrow \left| {m + 4} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = - 7\end{array} \right.\).
Cho parabol \(\left( P \right):y = {x^2} - 4x + 3\) và đường thẳng \(d:y = mx + 3\). Tìm giá trị thực của tham số \(m\) để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A,\;B\) có hoành độ \({x_1},\;{x_2}\) thỏa mãn \(x_1^3 + x_2^3 = 8\).
Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(d\) là \({x^2} - 4x + 3 = mx + 3\)
\( \Leftrightarrow x\left[ {x - \left( {m + 4} \right)} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = m + 4\end{array} \right.\).
Để \(d\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A,\;B\) khi và chỉ khi \(4 + m \ne 0 \Leftrightarrow m \ne - 4\).
Khi đó, ta có \(x_1^3 + x_2^3 = 8 \Leftrightarrow 0 + {\left( {4 + m} \right)^3} = 8\) \( \Leftrightarrow 4 + m = 2 \Leftrightarrow m = - 2\).
Tìm tất cả các giá trị thực của tham số \(m\) để phương trình \({x^2} - 5x + 7 + 2m = 0\) có nghiệm thuộc đoạn \(\left[ {1;5} \right]\).
Ta có \({x^2} - 5x + 7 + 2m = 0 \Leftrightarrow {x^2} - 5x + 7 = - 2m.\) \(\left( * \right)\)
Phương trình \(\left( * \right)\) là phương trình hoành độ giao điểm của parabol \(\left( P \right):{x^2} - 5x + 7\) và đường thẳng \(y = - 2m\) (song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số \(y = {x^2} - 5x + 7\) trên \(\left[ {1;5} \right]\) như sau:
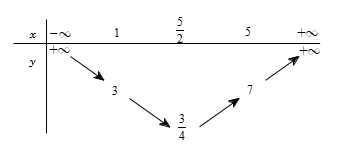
Dựa vào bảng biến ta thấy \(x \in \left[ {1;5} \right]\) thì \(y \in \left[ {\dfrac{3}{4};7} \right]\).
Do đó để phương trình \(\left( * \right)\) có nghiệm \(x \in \left[ {1;5} \right] \Leftrightarrow \dfrac{3}{4} \le - 2m \le 7 \Leftrightarrow - \dfrac{3}{8} \ge m \ge - \dfrac{7}{2}.\)
Biết rằng hàm số \(y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\) đạt giá trị nhỏ nhất bằng \(4\) tại \(x = 2\) và có đồ thị hàm số đi qua điểm \(A\left( {0;6} \right)\). Tính tích \(P = abc.\)
Hàm số đạt giá trị nhỏ nhất bằng \(4\) tại \(x = 2\) nên \(\left\{ \begin{array}{l}a > 0\\ - \dfrac{b}{{2a}} = 2\\ - \dfrac{\Delta }{{4a}} = 4\end{array} \right..\)
Đồ thị hàm số đi qua điểm \(A\left( {0;6} \right)\) nên ta có \(c = 6.\)
Từ đó ta có hệ \(\left\{ \begin{array}{l}a > 0\\ - \dfrac{b}{{2a}} = 2\\ - \dfrac{\Delta }{{4a}} = 4\\c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > 0\\b = - 4a\\{b^2} - 4ac = - 16a\\c = 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\b = - 4a\\16{a^2} - 8a = 0\\c = 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b = - 2\\c = 6\end{array} \right.\)
\( \Rightarrow P = abc = - 6.\)
Tìm tất cả các giá trị thực của tham số \(b\) để đồ thị hàm số \(y = - 3{x^2} + bx - 3\) cắt trục hoành tại hai điểm phân biệt.
Xét phương trình hoành độ giao điểm:\( - 3{x^2} + bx - 3 = 0.\) \(\left( 1 \right)\)
Để đồ thị hàm số cắt trục hoành tại hai điểm phân biệt khi và chỉ khi \(\left( 1 \right)\) có \(2\) nghiệm phân biệt \( \Leftrightarrow \Delta = {b^2} - 36 > 0 \Leftrightarrow \left[ \begin{array}{l}b < - 6\\b > 6\end{array} \right.\).
Biết đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) và đi qua điểm \(C\left( {0;\,\,5} \right).\) Tính tổng \(S = {a^2} + {b^2} + {c^2}.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) là parabol \( \Leftrightarrow a \ne 0.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) \( \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 1\\y\left( 1 \right) = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + c = 8\end{array} \right.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua \(C\left( {0;\,\,5} \right)\) \( \Leftrightarrow c = 5.\)
\( \Rightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + 5 = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\,\,\,\left( {tm} \right)\\b = 6\end{array} \right..\)
\( \Rightarrow S = {a^2} + {b^2} + {c^2}\) \( = {\left( { - 3} \right)^2} + {6^2} + {5^2} = 70.\)
Vậy \(S = 70.\)
Biết đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) và đi qua điểm \(C\left( {0;\,\,5} \right).\) Tính tổng \(S = {a^2} + {b^2} + {c^2}.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) là parabol \( \Leftrightarrow a \ne 0.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) \( \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 1\\y\left( 1 \right) = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + c = 8\end{array} \right.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua \(C\left( {0;\,\,5} \right)\) \( \Leftrightarrow c = 5.\)
\( \Rightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + 5 = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\,\,\,\left( {tm} \right)\\b = 6\end{array} \right..\)
\( \Rightarrow S = {a^2} + {b^2} + {c^2}\) \( = {\left( { - 3} \right)^2} + {6^2} + {5^2} = 70.\)
Vậy \(S = 70.\)
Biết đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) và đi qua điểm \(C\left( {0;\,\,5} \right).\) Tính tổng \(S = {a^2} + {b^2} + {c^2}.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) là parabol \( \Leftrightarrow a \ne 0.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) \( \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 1\\y\left( 1 \right) = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + c = 8\end{array} \right.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua \(C\left( {0;\,\,5} \right)\) \( \Leftrightarrow c = 5.\)
\( \Rightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + 5 = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\,\,\,\left( {tm} \right)\\b = 6\end{array} \right..\)
\( \Rightarrow S = {a^2} + {b^2} + {c^2}\) \( = {\left( { - 3} \right)^2} + {6^2} + {5^2} = 70.\)
Vậy \(S = 70.\)
Biết đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) và đi qua điểm \(C\left( {0;\,\,5} \right).\) Tính tổng \(S = {a^2} + {b^2} + {c^2}.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) là parabol \( \Leftrightarrow a \ne 0.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) \( \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 1\\y\left( 1 \right) = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + c = 8\end{array} \right.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua \(C\left( {0;\,\,5} \right)\) \( \Leftrightarrow c = 5.\)
\( \Rightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + 5 = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\,\,\,\left( {tm} \right)\\b = 6\end{array} \right..\)
\( \Rightarrow S = {a^2} + {b^2} + {c^2}\) \( = {\left( { - 3} \right)^2} + {6^2} + {5^2} = 70.\)
Vậy \(S = 70.\)
Biết đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) và đi qua điểm \(C\left( {0;\,\,5} \right).\) Tính tổng \(S = {a^2} + {b^2} + {c^2}.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) là parabol \( \Leftrightarrow a \ne 0.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) có đỉnh \(I\left( {1;\,\,8} \right)\) \( \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 1\\y\left( 1 \right) = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + c = 8\end{array} \right.\)
Đồ thị hàm số \(y = a{x^2} + bx + c\) đi qua \(C\left( {0;\,\,5} \right)\) \( \Leftrightarrow c = 5.\)
\( \Rightarrow \left\{ \begin{array}{l}b = - 2a\\a + b + 5 = 8\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}2a + b = 0\\a + b = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = - 3\,\,\,\left( {tm} \right)\\b = 6\end{array} \right..\)
\( \Rightarrow S = {a^2} + {b^2} + {c^2}\) \( = {\left( { - 3} \right)^2} + {6^2} + {5^2} = 70.\)
Vậy \(S = 70.\)

