Câu hỏi:
2 năm trước
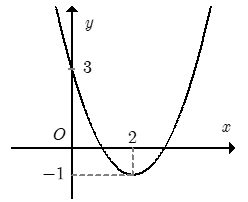
Cho hàm số \(f\left( x \right) = a{x^2} + bx + c\) đồ thị như hình. Hỏi với những giá trị nào của tham số thực \(m\) thì phương trình \(f\left( {\left| x \right|} \right) - 1 = m\) có đúng \(3\) nghiệm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: c
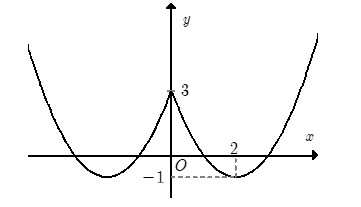
Ta có \(f\left( {\left| x \right|} \right) = f\left( x \right)\) nếu \(x \ge 0\). Hơn nữa hàm \(f\left( {\left| x \right|} \right)\) là hàm số chẵn. Từ đó suy ra cách vẽ đồ thị hàm số \(\left( C \right)\) từ đồ thị hàm số \(y = f\left( x \right)\) như sau:
+ Giữ nguyên đồ thị \(y = f\left( x \right)\) phía bên phải trục tung.
+ Lấy đối xứng phần đồ thị \(y = f\left( x \right)\) phía bên phải trục tung qua trục tung.
Kết hợp hai phần ta được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) như hình vẽ.
Phương trình
\(f\left( {\left| x \right|} \right) - 1 = m \Leftrightarrow f\left( {\left| x \right|} \right) = m + 1\) là phương trình hoành độ giao điểm của đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) và đường thẳng \(y = m + 1\) (song song hoặc trùng với trục hoành).
Dựa vào đồ thị, ta có yêu cầu bài toán \( \Leftrightarrow m + 1 = 3 \Leftrightarrow m = 2.\)
Hướng dẫn giải:
- Dựng đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) có được từ đồ thị hàm số \(y = f\left( x \right)\): Giữ nguyên phần đồ thị bên phải trục tung đồng thời lấy đối xứng phần đồ thị đó qua trục tung, xóa bỏ phần bên trái trục tung đi ta được đồ thị hàm số cần tìm.
