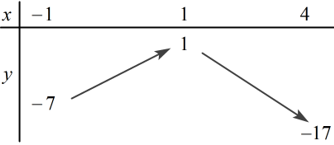
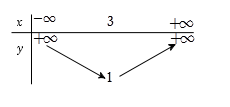
Gọi \(m;\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số: \(y = - 2{x^2} + 4x - 1,\,\,\forall x \in \left[ { - 1;4} \right]\). Tính tổng \(m + M?\)
Gọi \(I\left( {{x_I};{y_I}} \right)\) là đỉnh của đồ thị hàm số \(y = - 2{x^2} + 4x - 1\)\( \Rightarrow {x_I} = \dfrac{{ - b}}{{2a}} = 1 \in \left[ { - 1;4} \right]\)
Ta có BBT:
\( \Rightarrow \left\{ \begin{array}{l}M = \mathop {Max}\limits_{\left[ { - 1;\,\,4} \right]} y = 1\,\,\,khi\,\,\,x = 1\\m = \mathop {Min}\limits_{\left[ { - 1;\,\,4} \right]} y = - 17\,\,\,khi\,\,\,x = 4\end{array} \right.\) \( \Rightarrow M + m = 1 + \left( { - 17} \right) = - 16.\)
Tìm tọa độ đỉnh của parabol \(y = 2{x^2} + x + 2\)
\(y = 2{x^2} + x + 2\) có hoành độ đỉnh \({x_I} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 1}}{{2.2}} = \dfrac{{ - 1}}{4}\); tung độ đỉnh \({y_I} = 2{\left( {\dfrac{{ - 1}}{4}} \right)^2}\)\( + \dfrac{{ - 1}}{4} + 2 = \dfrac{{15}}{8}\)
Vậy đỉnh \(I\left( { - \dfrac{1}{4};\dfrac{{15}}{8}} \right)\)
Số các giá trị của tham số m để giá trị nhỏ nhất của hàm số \(f\left( x \right)=x{}^\text{2}+\left( 2m+1 \right)x+m{}^\text{2}-1\) trên đoạn $[0;1]$ bằng $1$ là
Ta có
\(\begin{array}{l} + )\,\, - \dfrac{b}{{2a}} = - \dfrac{{\left( {2m + 1} \right)}}{2} = \dfrac{{ - 2m - 1}}{2}\\ +) \,\,\,\Delta = {\left( {2m + 1} \right)^2} - 4\left( {{m^2} - 1} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = 4{m^2} + 4m + 1 - 4{m^2} + 4\\\,\,\,\,\,\,\,\,\,\,\,\, = 4m + 5\\\dfrac{{ - \Delta }}{{4a}} = \dfrac{{ - 4m - 5}}{4}\end{array}\)
Vậy đồ thị hàm số có đỉnh \(I\left( {\dfrac{{ - 2m - 1}}{2};\dfrac{{ - 4m - 5}}{4}} \right)\)
Vì \(a > 0\) nên đồ thị hàm số là parabol có bề lõm hướng lên trên và có điểm thấp nhất là đỉnh \(I\left( {\dfrac{{ - 2m - 1}}{2};\dfrac{{ - 4m - 5}}{4}} \right)\)
+) TH1
\(\begin{array}{l}\dfrac{{ - b}}{{2a}} \in \left[ {0;1} \right] \Leftrightarrow 0 \le \dfrac{{ - 2m - 1}}{2} \le 1\\ \Leftrightarrow 0 \le - 2m - 1 \le 2\\{\mkern 1mu} \Leftrightarrow 1 \le - 2m \le 3\\{\mkern 1mu} \Leftrightarrow \dfrac{{ - 1}}{2} \ge m \ge \dfrac{{ - 3}}{2}\end{array}\)
Khi đó \(\mathop {\min }\limits_{\left[ {0;1} \right]} f\left( x \right) = \dfrac{{ - \Delta }}{{4a}}\)\( = \dfrac{{ - 4m - 5}}{4} = 1\)
\( \Leftrightarrow - 4m - 5 = 4\)\( \Leftrightarrow m = \dfrac{{ - 9}}{4}\)\( \Leftrightarrow - 4m = 9\) (loại)
+) TH2: \(\dfrac{{ - b}}{{2a}} < 0 \Leftrightarrow \dfrac{{ - 2m - 1}}{2} < 0\)\( \Leftrightarrow m > \dfrac{{ - 1}}{2}\)
Khi đó \(\mathop {\min }\limits_{\left[ {0;1} \right]} f\left( x \right) = f(0)\)\( = {m^2} - 1 = 1\) \( \Leftrightarrow {m^2} = 2\)\( \Rightarrow m = \pm \sqrt 2 \)
Kết hợp với điều kiện \( \Rightarrow m = \sqrt 2 \)
+) TH3: \(\dfrac{{ - b}}{{2a}} > 1\)
\(\begin{array}{l} \Leftrightarrow \dfrac{{ - 2m - 1}}{2} > 1\\ \Leftrightarrow - 2m - 1 > 2\\ \Leftrightarrow - 2m > 3\\ \Leftrightarrow m < \dfrac{{ - 3}}{2}\end{array}\)
\(\begin{array}{l} \Rightarrow \mathop {\min }\limits_{\left[ {0;1} \right]} f\left( x \right) = f(1) \\= 1 + \left( {2m + 1} \right) + {m^2} - 1 \\= {m^2} + 2m + 1 = 1\\ \Leftrightarrow {m^2} + 2m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 2\end{array} \right.\end{array}\)
Kết hợp với điều kiện \(m = - 2\)
Vậy có 2 giá trị của m thỏa mãn.
Tìm m để giá trị nhỏ nhất của hàm số \(y = 4{x^2} - 4mx + {m^2} - m\) trên \(\mathbb{R}\) bằng 2
Do \(a = 4 > 0\) nên hàm số đạt giá trị nhỏ nhất \(y =- m\) tại \(x = \dfrac{m}{2}\).
Vậy \( m = - 2\)
Tìm m để giá trị lớn nhất của hàm số \(y = - 2{x^2} + 4mx + 5m - {m^2}\) trên \(\mathbb{R}\) bằng $6$.
Bước 1:
Do \(a = - 2 < 0\) nên hàm số đạt GTLN tại \(x =-\dfrac{4m}{2.(-2)}= m\).
Bước 2:
Khi đó \(y_{\max} =-2.m^2+4m.m+5m-m^2\)\(= {m^2} + 5m\)
Mà hàm số đạt giá trị lớn nhất trên $\mathbb{R}$ bằng 6.
\( \Rightarrow {m^2} + 5m = 6 \)
Bước 3:
\(\Leftrightarrow m^2+5m-6=0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - 6\end{array} \right.\)
Vậy có 2 giá trị của $m$ thỏa mãn bài toán là $m=1$ hoặc $m=-6$.
Cho hàm số \(y = {x^2} - 2x + 3\). Kết quả nào sau đây đúng trong các kết quả sau?
Do \(a > 0\) nên hàm số đạt giá trị nhỏ nhất \( - \dfrac{\Delta }{{4a}}\) tại \(x = - \dfrac{b}{{2a}}\).
Ta có: \(\Delta = {b^2} - 4ac = {\left( { - 2} \right)^2} - 4.3 = - 8 \Rightarrow - \dfrac{\Delta }{{4a}} = 2\).
\( - \dfrac{b}{{2a}} = 1\)
Vì vậy, hàm số đạt giá trị nhỏ nhất bằng 2 tại \(x = 1\).
Vậy \(\min f\left( x \right) = 2\) trên \(\mathbb{R}\)
Tìm a, c biết parabol (P): \(y = a{x^2} - 4x + c\) đi qua điểm \(A\left( {1;2} \right)\) và \(B\left( { - 2;5} \right)\).
Do A, B thuộc đồ thị (P), thay tọa độ của A, B vào phương trình của (P), ta được:
\(\left\{ \begin{array}{l}a.{\left( 1 \right)^2} - 4.1 + c = 2\\a.{\left( { - 2} \right)^2} - 4.\left( { - 2} \right) + c = 5\end{array} \right.\)
\(\begin{array}{l}\Leftrightarrow\left\{ \begin{array}{l}a - 4 + c = 2\\4a + 8 + c = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a+c = 6\\4a+c = -3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = - 3\\c = 9\end{array} \right.\end{array}\)
Vậy \(a = - 3;c = 9\).
Sử dụng MTCT casio fx 580 vnx giải hệ phương trình \(\left\{ \begin{array}{l}a+c = 6\\4a+c = -3\end{array} \right.\)
Bước 1: Chuyển sang chế độ giải hệ phương trình bậc nhất hai ẩn
Màn hình xuất hiện:
Bước 2: Nhập các hệ số vào tìm a và c
Trục đối xứng của parabol \(\left( P \right):y = 2{x^2} + 6x + 3\) là
Trục đối xứng \(x = - \dfrac{b}{{2a}} = - \dfrac{3}{2}\).
Trục đối xứng của parabol \(\left( P \right):y = - 2{x^2} + 5x + 3\) là
Ta có \(a=-2;b=5\).
Trục đối xứng là $x=-\dfrac{5}{-2.2}=\dfrac{5}{4}$
Một vật được ném lên trên cao và độ cao của nó so với mặt đất được cho bởi công thức \(h\left( t \right) = 5 + 4t - {t^2}\), với \(t\) là thời gian tính bằng giây (s) kể từ lúc bắt đầu ném. Độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng bao nhiêu mét?
Điền số nguyên hoặc phân số dạng a/b
Đáp án:
$m$
Đáp án:
$m$
Ta có hàm số \(h\left( t \right) = 5 + 4t - {t^2}\) có đồ thị là parabol có bề lõm hướng xuống và đạt giá trị lớn nhất tại thời điểm \(t = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 4}}{{2.\left( { - 1} \right)}} = 2\) (s).
Khi đó \(\max h\left( t \right) = h\left( 2 \right) = 5 + 4.2 - {2^2} = 9\) (m).
Vậy độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng 9 m.
Trong các hàm số sau, hàm số nào có đồ thị nhận đường \(x = 1\) làm trục đối xứng?
Xét đáp án A, ta có \( - \dfrac{b}{{2a}} = 1\).
Đỉnh của parabol \(\left( P \right):y = 3{x^2} - 2x + 1\) là
Parabol \(\left( P \right)\) có hoành độ đỉnh \(x = - \dfrac{b}{{2a}} = - \dfrac{{ - 2}}{{2.3}} = \dfrac{1}{3}\) \( \Rightarrow y = 3.{\left( {\dfrac{1}{3}} \right)^2} - 2.\dfrac{1}{3} + 1 = \dfrac{2}{3}\).
Vậy đỉnh \(I\left( {\dfrac{1}{3};\dfrac{2}{3}} \right)\).
Hàm số nào sau đây có đồ thị là parabol có đỉnh \(I\left( { - 1;3} \right)\)?
Đáp án A: Hoành độ đỉnh \(x = - \dfrac{{ - 4}}{{2.2}} = 1\) nên loại.
Đáp án B: Hoành độ đỉnh \(x = - \dfrac{{ - 2}}{{2.2}} = \dfrac{1}{2}\) nên loại.
Đáp án C: Hoành độ đỉnh \(x = - \dfrac{4}{{2.2}} = - 1\)\( \Rightarrow y = 2.{\left( { - 1} \right)^2} + 4.\left( { - 1} \right) + 5 = 3\) hay đỉnh \(\left( { - 1;3} \right)\).
Đáp án D: Hoành độ đỉnh \(x = - \dfrac{1}{{2.2}} = - \dfrac{1}{4}\) nên loại.
Tìm parabol \(\left( P \right):y = a{x^2} + 3x - 2,\) biết rằng parabol cắt trục \(Ox\) tại điểm có hoành độ bằng \(2.\)
Vì \(\left( P \right)\) cắt trục \(Ox\) tại điểm có hoành độ bằng \(2\) nên điểm \(A\left( {2;0} \right)\) thuộc \(\left( P \right)\).
Thay \(\left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right.\) vào \(\left( P \right)\), ta được \(0 = 4a + 6 - 2 \Leftrightarrow a = - 1\).
Vậy \(\left( P \right):y = - {x^2} + 3x - 2\).
Tìm giá trị thực của tham số \(m\) để parabol \(\left( P \right):y = m{x^2} - 2mx - 3m - 2\) \(\left( {m \ne 0} \right)\) có đỉnh thuộc đường thẳng \(y = 3x - 1\).
Hoành độ đỉnh của \(\left( P \right)\) là \(x = - \dfrac{b}{{2a}} = \dfrac{{2m}}{{2m}} = 1\).
Suy ra tung độ đỉnh \(y = - 4m - 2\). Do đó tọa độ đỉnh của \(\left( P \right)\) là \(I\left( {1; - 4m - 2} \right)\).
Theo giả thiết, đỉnh \(I\) thuộc đường thẳng \(y = 3x - 1\) nên \( - 4m - 2 = 3.1 - 1 \Leftrightarrow m = - 1.\)
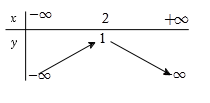
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
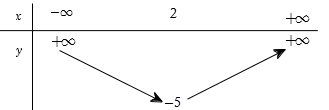
Nhận xét:
Bảng biến thiên có bề lõm hướng lên. Loại đáp án A và C.
Đỉnh của parabol có tọa độ là \(\left( {2; - 5} \right)\). Xét các đáp án còn lại, đáp án B thỏa mãn.
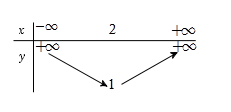
Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?
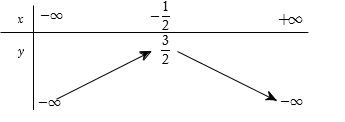
Nhận xét:
Bảng biến thiên có bề lõm hướng xuống. Loại đáp án A và B.
Đỉnh của parabol có tọa độ là \(\left( { - \dfrac{1}{2};\dfrac{3}{2}} \right)\). Xét các đáp án còn lại, đáp án D thỏa mãn.
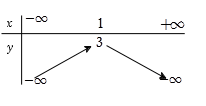
Bảng biến thiên của hàm số \(y = - 2{x^2} + 4x + 1\) là bảng nào trong các bảng được cho sau đây ?
Hệ số \(a = - 2 < 0\) suy ra bề lõm hướng xuống. Loại B, D.
Ta có \( - \dfrac{b}{{2a}} = 1\) và \(y\left( 1 \right) = 3\). Do đó C thỏa mãn.
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = f\left( x \right) = {x^2} - 3x\) trên đoạn \(\left[ {0;2} \right].\)
Hàm số \(y = {x^2} - 3x\) có \(a = 1 > 0\) nên bề lõm hướng lên.
Hoành độ đỉnh \(x = - \dfrac{b}{{2a}} = \dfrac{3}{2} \in \left[ {0;2} \right]\).
Vậy \(\left\{ \begin{array}{l}m = \min y = f\left( {\dfrac{3}{2}} \right) = - \dfrac{9}{4}\\M = \max y = \max \left\{ {f\left( 0 \right),f\left( 2 \right)} \right\} = \max \left\{ {0, - 2} \right\} = 0\end{array} \right..\)
Tìm giá trị lớn nhất \(M\) và giá trị nhỏ nhất \(m\) của hàm số \(y = f\left( x \right) = - {x^2} - 4x + 3\) trên đoạn \(\left[ {0;4} \right].\)
Hàm số \(y = - {x^2} - 4x + 3\) có \(a = - 1 < 0\) nên bề lõm hướng xuống.
Hoành độ đỉnh \(x = - \dfrac{b}{{2a}} = - 2 \notin \left[ {0;4} \right]\).
Ta có \(\left\{ \begin{array}{l}f\left( 4 \right) = - 29\\f\left( 0 \right) = 3\end{array} \right.\)\( \Rightarrow m = \min y = f\left( 4 \right) = - 29;\) \(M = \max y = f\left( 0 \right) = 3\)