Câu hỏi:
2 năm trước
Gọi \(m;\,\,M\) lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số: \(y = - 2{x^2} + 4x - 1,\,\,\forall x \in \left[ { - 1;4} \right]\). Tính tổng \(m + M?\)
Trả lời bởi giáo viên
Đáp án đúng: d
Gọi \(I\left( {{x_I};{y_I}} \right)\) là đỉnh của đồ thị hàm số \(y = - 2{x^2} + 4x - 1\)\( \Rightarrow {x_I} = \dfrac{{ - b}}{{2a}} = 1 \in \left[ { - 1;4} \right]\)
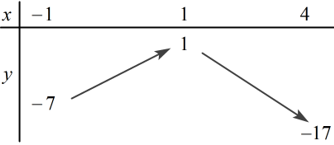
Ta có BBT:
\( \Rightarrow \left\{ \begin{array}{l}M = \mathop {Max}\limits_{\left[ { - 1;\,\,4} \right]} y = 1\,\,\,khi\,\,\,x = 1\\m = \mathop {Min}\limits_{\left[ { - 1;\,\,4} \right]} y = - 17\,\,\,khi\,\,\,x = 4\end{array} \right.\) \( \Rightarrow M + m = 1 + \left( { - 17} \right) = - 16.\)
Hướng dẫn giải:
Xét hàm số \(y = - 2{x^2} + 4x - 1,\) vẽ bảng biến thiên của hàm số trên \(\left[ { - 1;\,4} \right]\) rồi kết luận GTLN, GTNN của hàm số và tính giá trị biểu thức \(M + m.\)
