Đại cương về hàm số

Ta có:\(\left\{ \begin{array}{l}f\left( 5 \right) = \dfrac{{\sqrt {5 + 4}  - 1}}{{5 - 1}} = \dfrac{1}{2}\\f\left( { - 5} \right) = 3 - \left( { - 5} \right) = 8\end{array} \right.\) \( \Rightarrow f\left( 5 \right) + f\left( { - 5} \right) = \dfrac{1}{2} + 8 = \dfrac{{17}}{2}.\)

Điều kiện:

\(\left\{ \begin{array}{l}x - 3m + 1 \ge 0\\x + m - 5 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 3m - 1\\x > 5 - m\end{array} \right.\)(1)

Trường hợp 1: \(3m - 1 \ge 5 - m \Leftrightarrow m \ge \dfrac{3}{2}\)(*)

Khi đó \((1) \Leftrightarrow x \ge 3m - 1\)\( \Rightarrow \)TXĐ: \(D = \left[ {3m - 1; + \infty } \right)\)

Hàm số xác định trên \(\left( {5;7} \right)\) khi và chỉ khi \(\left( {5;7} \right) \subset \left[ {3m - 1; + \infty } \right)\).

\( \Leftrightarrow 3m - 1 \le 5\)\( \Leftrightarrow m \le 2\). Kết hợp với (*)  ta được: \(\dfrac{3}{2} \le m \le 2\).

Trường hợp 2: \(3m - 1 < 5 - m \Leftrightarrow m < \dfrac{3}{2}\)(**)

Khi đó \((1) \Leftrightarrow x > 5 - m\)\( \Rightarrow \)TXĐ: \(D = \left( {5 - m; + \infty } \right)\)

Hàm số xác định trên \(\left( {5;7} \right)\) khi và chỉ khi \(\left( {5;7} \right) \subset \left( {5 - m; + \infty } \right)\).

\( \Leftrightarrow 5 - m \le 5 \Leftrightarrow m \ge 0\). Kết hợp với (**)  ta được: \(0 \le m < \dfrac{3}{2}\).

Kết hợp 2 trường hợp ta được \(0 \le m \le 2\).

Gọi \(\overrightarrow v \left( {a;b} \right)\) là vectơ tịnh tiến. \(M\left( {x;y} \right) \in (P)\) tùy ý, \(M'\left( {x';y'} \right)\) là ảnh của \(M\) qua \({T_{\overrightarrow v }}\), khi đó:

\(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

\(\overrightarrow v \left( {a;b} \right)\) là vectơ tịnh tiến biến \(\left( P \right)\) thành \(\left( {P'} \right)\) khi và chỉ khi \(M' \in (P')\).

 \( \Leftrightarrow {\left( {x + a} \right)^2} - 2\left( {x + a} \right) + 5 = y + b\)

\( \Leftrightarrow y = {x^2} + \left( {2a - 2} \right)x + {a^2} - 2a + 5 - b\)

Mà ta có \(M \in \left( P \right)\) nên \(y = {x^2} + 5\). Đồng nhất hệ số ta được:

\(\left\{ \begin{array}{l}2a - 2 = 0\\{a^2} - 2a + 5 - b = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 1\end{array} \right.\)

Vậy \(\overrightarrow v  = \left( {1; - 1} \right)\)

Xét đáp án A, thay \(x = 2\) và \(y = 1\)

vào hàm số \(y = \dfrac{1}{{x - 1}}\) ta được \(1 = \dfrac{1}{{2 - 1}}\): thỏa mãn.

Xét đáp án A, thay \(x = 2\) và \(y = 0\) vào hàm số \(y = \dfrac{{\sqrt {{x^2} - 4x + 4} }}{x}\) ta được \(0 = \dfrac{{\sqrt {{2^2} - 4.2 + 4} }}{2}\): thỏa mãn.

Xét đáp án B, thay \(x = 3\) và \(y = \dfrac{1}{3}\) vào hàm số \(y = \dfrac{{\sqrt {{x^2} - 4x + 4} }}{x}\) ta được \(\dfrac{1}{3} = \dfrac{{\sqrt {{3^2} - 4.3 + 4} }}{3}\): thỏa mãn.

Xét đáp án C, thay \(x = 1\) và \(y =  - 1\) vào hàm số

\(y = \dfrac{{\sqrt {{x^2} - 4x + 4} }}{x}\) ta được \( - 1 = \dfrac{{\sqrt {{1^2} - 4.1 + 4} }}{1} \Leftrightarrow  - 1 = 1\): không thỏa mãn.

Ta có · \(f\left( { - 1} \right) = \left| { - 5.\left( { - 1} \right)} \right| = \left| 5 \right| = 5 \Rightarrow \)A đúng.

\(f\left( 2 \right) = \left| { - 5.2} \right| = \left| { - 10} \right| = 10 \Rightarrow \)B đúng.

\(f\left( { - 2} \right) = \left| { - 5.\left( { - 2} \right)} \right| = \left| {10} \right| = 10 \Rightarrow \)C đúng.

\(f\left( {\dfrac{1}{5}} \right) = \left| { - 5.\dfrac{1}{5}} \right| = \left| { - 1} \right| = 1 \Rightarrow \)D sai. 

Hàm số xác định khi \(2x - 2 \ne 0 \Leftrightarrow x \ne 1\).

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ 1 \right\}\).

Hàm số xác định khi \({x^3} - 3x + 2 \ne 0 \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} + x - 2} \right) \ne 0\)

      \( \Leftrightarrow \left\{ \begin{array}{l}x - 1 \ne 0\\{x^2} + x - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\\left\{ \begin{array}{l}x \ne 1\\x \ne  - 2\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\x \ne  - 2\end{array} \right..\)

Vậy tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ { - 2;1} \right\}\)

Hàm số xác định khi \(\left\{ \begin{array}{l}x + 2 \ge 0\\x + 3 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge  - 2\\x \ge  - 3\end{array} \right. \Leftrightarrow x \ge  - 2\).

Vậy tập xác định của hàm số là \({\rm{D}} = \left[ { - 2; + \infty } \right)\).

Hàm số xác định khi \(\left\{ \begin{array}{l}3x - 2 \ge 0\\4 - 3x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{2}{3}\\x < \dfrac{4}{3}\end{array} \right. \Leftrightarrow \dfrac{2}{3} \le x < \dfrac{4}{3}.\)

Vậy tập xác định của hàm số là \({\rm{D}} = \left[ {\dfrac{2}{3};\dfrac{4}{3}} \right)\).

Hàm số xác định khi \(\left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\2 - x \ne 0\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\2 - x \ge 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x \ne 2\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x \le 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x \ne 2\end{array} \right.\\x < 1\end{array} \right.\).

Vậy xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ 2 \right\}\).

Hàm số xác định khi \(\left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x \ne 0\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x + 1 \ge 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\\left\{ \begin{array}{l}x < 1\\x \ge  - 1\end{array} \right.\end{array} \right.\).

Vậy tập xác định của hàm số là \({\rm{D}} = \left[ { - 1; + \infty } \right)\).

Hàm số xác định khi \(\left\{ \begin{array}{l}x - m + 1 \ge 0\\ - x + 2m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m - 1\\x < 2m\end{array} \right..\)

\( \Rightarrow \) Tập xác định của hàm số là \({\rm{D}} = \left[ {m - 1;2m} \right)\) với điều kiện \(m - 1 < 2m \Leftrightarrow m >  - 1.\)

Hàm số đã cho xác định trên \(\left( { - 1;3} \right)\) khi và chỉ khi \(\left( { - 1;3} \right) \subset \left[ {m - 1;2m} \right)\)

\( \Leftrightarrow m - 1 \le  - 1 < 3 \le 2m \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge \dfrac{3}{2}\end{array} \right. \Leftrightarrow m \in \emptyset .\)

Hàm số xác định khi \(x - m \ne 0 \Leftrightarrow x \ne m.\)

\( \Rightarrow \) Tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ m \right\}\).

Hàm số xác định trên \(\left( { - 1;0} \right)\) khi và chỉ khi \(m \notin \left( { - 1;0} \right) \Leftrightarrow \left[ \begin{array}{l}m \ge 0\\m \le  - 1\end{array} \right.\).

Hàm số xác định khi \(x - m \ne 0 \Leftrightarrow x \ne m.\)

\( \Rightarrow \) Tập xác định của hàm số là \({\rm{D}} = \mathbb{R}\backslash \left\{ m \right\}\).

Hàm số xác định trên \(\left( { - 1;0} \right)\) khi và chỉ khi \(m \notin \left( { - 1;0} \right) \Leftrightarrow \left[ \begin{array}{l}m \ge 0\\m \le  - 1\end{array} \right.\).

Hàm số xác định khi \(\left\{ \begin{array}{l}x - m + 2 \ge 0\\\sqrt {x - m + 2}  - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m - 2\\x \ne m - 1\end{array} \right.\).

\( \Rightarrow \) Tập xác định của hàm số là \({\rm{D}} = \left[ {m - 2; + \infty } \right)\backslash \left\{ {m - 1} \right\}\).

Hàm số xác định trên \(\left( {0;1} \right)\) khi và chỉ khi \(\left( {0;1} \right) \subset \left[ {m - 2; + \infty } \right)\backslash \left\{ {m - 1} \right\}\)

\( \Leftrightarrow \left[ \begin{array}{l}m - 2 \le 0 < 1 \le m - 1\\m - 1 \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m \le 2\\m \ge 2\end{array} \right.\\m \le 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\\m \le 1\end{array} \right.\).

Hàm số xác định khi \(\left\{ \begin{array}{l}x - m \ge 0\\2x - m - 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge m\\x \ge \dfrac{{m + 1}}{2}\end{array} \right. \left(  *  \right)\).

TH1: Nếu \(m \ge \dfrac{{m + 1}}{2} \Leftrightarrow m \ge 1\) thì \(\left(  *  \right) \Leftrightarrow x \ge m\).

\( \Rightarrow \) Tập xác định của hàm số là \({\rm{D}} = \left[ {m; + \infty } \right)\).

Khi đó, hàm số xác định trên \(\left( {0; + \infty } \right)\) khi và chỉ khi \(\left( {0; + \infty } \right) \subset \left[ {m; + \infty } \right) \Leftrightarrow m \le 0\)

\( \Rightarrow \) Không thỏa mãn điều kiện \(m \ge 1\).

TH2: Nếu \(m \le \dfrac{{m + 1}}{2} \Leftrightarrow m \le 1\) thì \(\left(  *  \right) \Leftrightarrow x \ge \dfrac{{m + 1}}{2}\).

\( \Rightarrow \) Tập xác định của hàm số là \({\rm{D}} = \left[ {\dfrac{{m + 1}}{2}; + \infty } \right)\).

Khi đó, hàm số xác định trên \(\left( {0; + \infty } \right)\) khi và chỉ khi \(\left( {0; + \infty } \right) \subset \left[ {\dfrac{{m + 1}}{2}; + \infty } \right)\) \( \Leftrightarrow \dfrac{{m + 1}}{2} \le 0 \Leftrightarrow m \le  - 1\)

\( \Rightarrow \) Thỏa mãn điều kiện \(m \le 1\).  Vậy \(m \le  - 1\) thỏa yêu cầu bài toán.

Hàm số xác định khi \({x^2} - 6x + m - 2 > 0 \Leftrightarrow {\left( {x - 3} \right)^2} + m - 11 > 0\).

Hàm số xác định với \(\forall x \in \mathbb{R} \Leftrightarrow {\left( {x - 3} \right)^2} + m - 11 > 0\) đúng với mọi \(x \in \mathbb{R}\)

\( \Leftrightarrow m - 11 > 0 \Leftrightarrow m > 11\).

Trên khoảng \(\left( { - 3; - 1} \right)\) và \(\left( {1;3} \right)\) đồ thị hàm số đi lên từ trái sang phải

\( \Rightarrow \) Hàm số đồng biến trên khoảng \(\left( { - 3; - 1} \right)\) và \(\left( {1;3} \right).\)

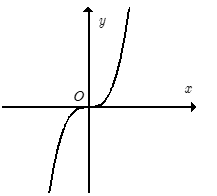
Quan sát đồ thị hàm số ta thấy, hàm số đồng biến trên \(\mathbb{R}\) nên các đáp án A, B, C đều đúng.

Đáp án D sai vì không có khái niệm hàm số đồng biến tại một điểm.