Tổng hợp câu hay và khó chương 7

M, G, I thẳng hàng $\Leftrightarrow$ tồn tại số k để $\overrightarrow {IG}  = k\overrightarrow {IM}$

$\begin{array}{l}\overrightarrow {IG}  = \dfrac{1}{3}\left( {\overrightarrow {IA}  + \overrightarrow {IB}  + \overrightarrow {IC} } \right) = \dfrac{1}{3}\overrightarrow {IA}  + \dfrac{1}{3}\left( {\overrightarrow {IA}  + \overrightarrow {AB} } \right) + \dfrac{1}{3}\left( {\overrightarrow {IA}  + \overrightarrow {AC} } \right)\\ = \overrightarrow {IA}  + \dfrac{1}{3}\overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {AC}  = \dfrac{5}{6}\overrightarrow {AC}  + \dfrac{1}{3}\overrightarrow {AB} \end{array}$

$\overrightarrow {IM}  = \overrightarrow {IA}  + \overrightarrow {AM}  = \dfrac{1}{2}\overrightarrow {AC}  + x\overrightarrow {AB}$

Do đó $\dfrac{5}{6}\overrightarrow {AC}  + \dfrac{1}{3}\overrightarrow {AB}  = k\left( {\dfrac{1}{2}\overrightarrow {AC}  + x\overrightarrow {AB} } \right) = \dfrac{k}{2}\overrightarrow {AC}  + kx\overrightarrow {AB}$.

Đồng nhất hệ số ta được $\left\{ \begin{array}{l}k = \dfrac{5}{3}\\x = \dfrac{1}{5}\end{array} \right.$

Ta có:${G_1}$  trọng tâm tam giác ABN $\Rightarrow \overrightarrow {A{G_1}}  = \dfrac{2}{3}\overrightarrow {AM} .$

${G_2}$  trọng tâm tam giác ACM $\Rightarrow \overrightarrow {A{G_2}}  = \dfrac{2}{3}\overrightarrow {AN} .$

$\begin{array}{l} \Rightarrow \overrightarrow {{G_1}{G_2}}  = \overrightarrow {{G_1}A}  + \overrightarrow {A{G_2}}  =  - \dfrac{2}{3}\overrightarrow {AM}  + \dfrac{2}{3}\overrightarrow {AN} \\ =  - \dfrac{2}{3}\left( {\overrightarrow {AB}  + \overrightarrow {BM} } \right) + \dfrac{2}{3}\left( {\overrightarrow {AC}  + \overrightarrow {CN} } \right)\\ =  - \dfrac{2}{3}\overrightarrow {AB}  - \dfrac{2}{3}.\dfrac{1}{3}\overrightarrow {BC}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{2}{3}.\dfrac{1}{3}\overrightarrow {BC} \\ =  - \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{4}{9}\overrightarrow {BC} \\ =  - \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{4}{9}\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)\end{array}$

$\begin{array}{l} =  - \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{2}{3}\overrightarrow {AC}  - \dfrac{4}{9}\overrightarrow {AC}  + \dfrac{4}{9}\overrightarrow {AB} \\ =  - \dfrac{2}{9}\overrightarrow {AB}  + \dfrac{2}{9}\overrightarrow {AC} .\\ \Rightarrow \left\{ \begin{array}{l}x =  - \dfrac{2}{9}\\y = \dfrac{2}{9}\end{array} \right. \Rightarrow x + y =  - \dfrac{2}{9} + \dfrac{2}{9} = 0.\end{array}$

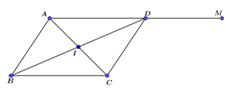
Ta có $I$ là trung điểm của $AC$ $\Rightarrow C\left( { - 4;{\rm{ }} - 1} \right)$.

Điểm $D$ có tung độ gấp đôi hoành độ $\Rightarrow D\left( {{x_D};2{x_D}} \right)$.

Lại có $\overrightarrow {AM}  = \left( {2;{\rm{ }}6} \right)$, $\overrightarrow {AD}  = \left( {{x_D} - 2;{\rm{ }}2{x_D} - 3} \right)$.

Mà $A$, $M$, $D$ thẳng hàng $\Rightarrow 6\left( {{x_D} - 2} \right) = 2\left( {2{x_D} - 3} \right)$ $\Leftrightarrow {x_D} = 3$ $\Rightarrow D\left( {3;{\rm{ }}6} \right)$.

$I$ là trung điểm $BD$ $\Rightarrow B\left( { - 5;{\rm{ }} - 4} \right)$.

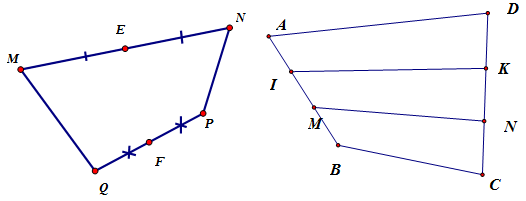
Bước 1:

Ta chứng minh bài toán sau:

Gọi $E$, $F$ lần lượt là trung điểm của $MN$, $PQ$ thì ta có: $\overrightarrow {EF}  = \dfrac{1}{2}\left( {\overrightarrow {MQ}  + \overrightarrow {NP} } \right)$.

Thật vậy, ta có: $\overrightarrow {EF}  = \dfrac{1}{2}\left( {\overrightarrow {EP}  + \overrightarrow {EQ} } \right)$$= \dfrac{1}{2}\left( {\overrightarrow {EN}  + \overrightarrow {NP}  + \overrightarrow {EM}  + \overrightarrow {MQ} } \right)$$= \dfrac{1}{2}\left( {\overrightarrow {MQ}  + \overrightarrow {NP} } \right)$

Bước 2: 

Gọi $I$, $K$ lần lượt là trung điểm của $AM$ và $DN$.

$\Rightarrow \overrightarrow {IK}  = \dfrac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {MN} } \right)$

Bước 3:

Khi đó M là trung điểm của IB và N là trung điểm của KC.

Áp dụng kết quả của bài toán trên ta có: $\overrightarrow {MN}  = \dfrac{1}{2}\left( {\overrightarrow {BC}  + \overrightarrow {IK} } \right)$$= \dfrac{1}{2}\left( {\overrightarrow {BC}  + \dfrac{1}{2}\left( {\overrightarrow {AD}  + \overrightarrow {MN} } \right)} \right)$

$= \dfrac{1}{2}\left( {\overrightarrow {BC}  + \dfrac{1}{2}\overrightarrow {AD}  + \dfrac{1}{2}\overrightarrow {MN} } \right)$$= \dfrac{1}{2}\overrightarrow {BC}  + \dfrac{1}{4}\overrightarrow {AD}  + \dfrac{1}{4}\overrightarrow {MN}$

$\Rightarrow \dfrac{3}{4}\overrightarrow {MN}  = \dfrac{1}{2}\overrightarrow {BC}  + \dfrac{1}{4}\overrightarrow {AD}$

$\Rightarrow \overrightarrow {MN}  = \dfrac{1}{3}\overrightarrow {AD}  + \dfrac{2}{3}\overrightarrow {BC}$.

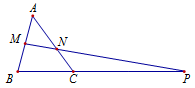
Cách 1: Tự luận:

Ta có   $\overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM}  = \dfrac{3}{5}\overrightarrow {AC}  - \dfrac{1}{2}\overrightarrow {AB}$$\left( 1 \right)$

            $\overrightarrow {NP}  = \overrightarrow {NC}  + \overrightarrow {CP}  = \dfrac{2}{5}\overrightarrow {AC}  + \left( {\overrightarrow {BP}  - \overrightarrow {BC} } \right)$

                   $= \dfrac{2}{5}\overrightarrow {AC}  + \left( {\dfrac{1}{k} - 1} \right)\overrightarrow {BC}$

                   $= \dfrac{2}{5}\overrightarrow {AC}  + \left( {\dfrac{1}{k} - 1} \right)\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)$

                   $= \left( {\dfrac{1}{k} - \dfrac{2}{5}} \right)\overrightarrow {AC}  - \left( {\dfrac{1}{k} - 1} \right)\overrightarrow {AB}$

Để ba điểm $M$, $N$, $P$ thẳng hàng thì $\exists m \in \mathbb{R}:\overrightarrow {NP}  = m\overrightarrow {MN}$

$\Leftrightarrow \left( {\dfrac{1}{k} - \dfrac{3}{5}} \right)\overrightarrow {AC}  - \left( {\dfrac{1}{k} - 1} \right)\overrightarrow {AB}  = \dfrac{{3m}}{5}\overrightarrow {AC}  - \dfrac{m}{2}\overrightarrow {AB}$

Điều kiện: $\left\{ \begin{array}{l}\dfrac{1}{k} - \dfrac{3}{5} = \dfrac{{3m}}{5}\\ - \left( {\dfrac{1}{k} - 1} \right) =  - \dfrac{m}{2}\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}m = 4\\k = \dfrac{1}{3}\end{array} \right.$.

Vậy $k = \dfrac{1}{3}$.

Cách 2: Trắc nghiệm:

Ta có   $\overrightarrow {MA\,}  + \overrightarrow {MB\,}  = \overrightarrow {0\,}  \Leftrightarrow \overrightarrow {MA\,}  =  - \overrightarrow {MB\,}  \Rightarrow \dfrac{{\overline {MA} }}{{\overline {MB} }} =  - 1$

$\overrightarrow {BC\,}  = k\overrightarrow {BP\,}  \Leftrightarrow \overrightarrow {PB\,}  = \left( {1 - k} \right)\overrightarrow {PC\,}  \Rightarrow \dfrac{{\overline {PB} }}{{\overline {PC} }} = 1 - k$

            $2\overrightarrow {NA\,}  + 3\overrightarrow {NC}  = \overrightarrow {0\,}  \Leftrightarrow 2\overrightarrow {NA\,}  =  - \dfrac{3}{2}\overrightarrow {NC\,}  \Rightarrow \dfrac{{\overline {NA} }}{{\overline {NC} }} =  - \dfrac{3}{2}$

Theo định lí Mêlêxauýt ba điểm $M$, $N$, $P$ thẳng hàng khi

$\dfrac{{\overline {MA} }}{{\overline {MB} }} \cdot \dfrac{{\overline {PB} }}{{\overline {PC} }} \cdot \dfrac{{\overline {NC} }}{{\overline {NA} }} = 1$$\Leftrightarrow \left( { - 1} \right).\left( {1 - k} \right).\left( { - \dfrac{3}{2}} \right) = 1 \Leftrightarrow k = \dfrac{1}{3}$.

Vậy $k = \dfrac{1}{3}$.

$\left| {\overrightarrow a  - 2\overrightarrow b } \right| = \sqrt {15}  \Leftrightarrow {\left| {\overrightarrow a } \right|^2} + 4{\left| {\overrightarrow b } \right|^2} - 4\overrightarrow a \overrightarrow b  = 15 \Leftrightarrow 2\overrightarrow a \overrightarrow b  = 1$.

$\overrightarrow u \overrightarrow v  = \left( {\overrightarrow a  + \overrightarrow b } \right)\left( {2k\overrightarrow a  - \overrightarrow b } \right) = 2k{\left| {\overrightarrow a } \right|^2} - {\left| {\overrightarrow b } \right|^2} + \left( {2k - 1} \right)\overrightarrow a \overrightarrow b  = 2k - 4 + \dfrac{{2k - 1}}{2}$.

${\left( {\left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right|} \right)^2} = {\left( {\left| {\left( {\overrightarrow a  + \overrightarrow b } \right)} \right|\left| {\left( {2k\overrightarrow a  - \overrightarrow b } \right)} \right|} \right)^2}$$= \left( {{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} + 2\overrightarrow a \overrightarrow b } \right)\left( {4{k^2}{{\left| {\overrightarrow a } \right|}^2} + {{\left| {\overrightarrow b } \right|}^2} - 4k\overrightarrow a \overrightarrow b } \right)$$= \left( {5 + 2\overrightarrow a \overrightarrow b } \right)\left( {4{k^2} + 4 - 4k\overrightarrow a \overrightarrow b } \right)$$= 6\left( {4{k^2} + 4 - 2k} \right)$$\Rightarrow \left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right| = \sqrt {6\left( {4{k^2} + 4 - 2k} \right)}$.

$\left( {\overrightarrow u ,\overrightarrow v } \right) = 60^\circ$$\Rightarrow \cos \left( {60^\circ } \right) = \dfrac{{\overrightarrow u \overrightarrow v }}{{\left| {\overrightarrow u } \right|\left| {\overrightarrow v } \right|}}$$\Leftrightarrow \dfrac{1}{2} = \dfrac{{2k - 4 + \dfrac{{2k - 1}}{2}}}{{\sqrt {6\left( {4{k^2} + 4 - 2k} \right)} }}$$\Leftrightarrow \sqrt {6\left( {4{k^2} + 4 - 2k} \right)}  = 6k - 9$

$\Leftrightarrow \sqrt {6\left( {4{k^2} + 4 - 2k} \right)}  = 6k - 9$$\Leftrightarrow \left\{ \begin{array}{l}k \ge \dfrac{3}{2}\\\sqrt {6\left( {4{k^2} + 2 - k} \right)}  = 6k - 9\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}k \ge \dfrac{3}{2}\\12{k^2} - 96k + 57 = 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}k \ge \dfrac{3}{2}\\k = 4 \pm \dfrac{{3\sqrt 5 }}{2}\end{array} \right.$$\Leftrightarrow k = 4 + \dfrac{{3\sqrt 5 }}{2}$.

Ta có $\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AD}  + \overrightarrow {DN}$$= \dfrac{2}{3}\overrightarrow {BA}  + \overrightarrow {AD}  + \dfrac{2}{3}\overrightarrow {DC}$

$= \dfrac{2}{3}\left( {\overrightarrow {BC}  + \overrightarrow {CA} } \right) + \overrightarrow {AD}  + \dfrac{2}{3}\left( {\overrightarrow {DA}  + \overrightarrow {AC} } \right)$$= \dfrac{2}{3}\overrightarrow {BC}  + \overrightarrow {AD}  - \dfrac{2}{3}\overrightarrow {AD}$$= \dfrac{1}{3}\overrightarrow {AD}  + \dfrac{2}{3}\overrightarrow {BC}$.

Cách 1: Do $M$ trên trục hoành $\Rightarrow M\left( {x;0} \right)$, $\overrightarrow {AB}  = \left( {1; - 1} \right)$$\Rightarrow AB = \sqrt 2$.

$\overrightarrow {AM}  = \left( {x - 2;3} \right)$, $\overrightarrow {BM}  = \left( {x - 3;4} \right)$

Ta có chu vi tam giác $AMB$: ${P_{ABM}} = \sqrt 2  + \sqrt {{{\left( {x - 2} \right)}^2} + {3^2}}  + \sqrt {{{\left( {x - 3} \right)}^2} + {4^2}}$

$= \sqrt 2  + \sqrt {{{\left( {x - 2} \right)}^2} + {3^2}}  + \sqrt {{{\left( {3 - x} \right)}^2} + {4^2}}$$\ge \sqrt 2  + \sqrt {{{\left( {x - 2 + 3 - x} \right)}^2} + {{\left( {3 + 4} \right)}^2}}$

$\Leftrightarrow {P_{ABM}} \ge 6\sqrt 2$. Dấu bằng xảy ra khi $\dfrac{{x - 2}}{{3 - x}} = \dfrac{3}{4}$$\Leftrightarrow x = \dfrac{{17}}{7}$$\Rightarrow M\left( {\dfrac{{17}}{7};0} \right)$.

Cách 2: Lấy đối xứng $A$ qua $Ox$ ta được $A'\left( {2;3} \right)$. Ta có $MA + MB = MA' + MB \ge A'B$.

Dấu bằng xảy ra khi $M$ trùng với giao điểm của $A'B$ với $Ox$.

Do $E \in Ox$ $\Rightarrow E\left( {a;\,0} \right)$.

Ta có: $\overrightarrow {EM\,}  = \left( { - 1 - a;\, - 2} \right)$; $\overrightarrow {EN\,}  = \left( {3 - a;\,2} \right)$; $\overrightarrow {EP\,}  = \left( {4 - a;\, - 1} \right)$

Suy ra $\overrightarrow {EM}  + \overrightarrow {EN}  + \overrightarrow {EP}  = \left( {6 - 3a;\, - 1} \right)$.

Do đó: $\left| {\overrightarrow {EM}  + \overrightarrow {EN}  + \overrightarrow {EP} } \right| = \sqrt {{{\left( {6 - 3a} \right)}^2} + {{\left( { - 1} \right)}^2}}$$= \sqrt {{{\left( {6 - 3a} \right)}^2} + 1}  \ge 1$.

Giá trị nhỏ nhất của $\left| {\overrightarrow {EM}  + \overrightarrow {EN}  + \overrightarrow {EP} } \right|$ bằng $1$.

Dấu  xảy ra khi và chỉ khi $6 - 3a = 0$ $\Leftrightarrow a = 2$.

Vậy $E\left( {2;0} \right)$.

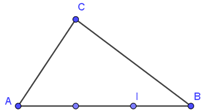
Gọi $I$ là điểm trên cạnh $AB$ sao cho $3\overrightarrow {BI}  = \overrightarrow {BA}$, ta có:

$\overrightarrow {MA}  + 2\overrightarrow {MB}$$= \overrightarrow {MB}  + \overrightarrow {BA}  + 2\overrightarrow {MB}$$= 3\overrightarrow {MB}  + \overrightarrow {BA}$$= 3\overrightarrow {MB}  + 3\overrightarrow {BI}$$= 3\overrightarrow {MI}$.

$\overrightarrow {MA}  - \overrightarrow {MB}  = \overrightarrow {BA}$.

$\left| {\overrightarrow {MA}  + 2\overrightarrow {MB} } \right| = 6\left| {\overrightarrow {MA}  - \overrightarrow {MB} } \right|$ $\Leftrightarrow \left| {3\overrightarrow {MI} } \right| = 6\left| {\overrightarrow {BA} } \right|$ $\Leftrightarrow MI = 2AB$.

Vậy $M$ nằm trên đường tròn tâm $I$, bán kính $R = 2AB$ với $I$ nằm trên cạnh $AB$ sao cho $IA = 2IB$.

Ta có: $4\overrightarrow {BM}  - 3\overrightarrow {BC}  = \overrightarrow 0$ $\Leftrightarrow 4\left( {\overrightarrow {AM}  - \overrightarrow {AB} } \right) - 3\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right) = \overrightarrow 0$

$\Leftrightarrow 4\overrightarrow {AM}  - 4\overrightarrow {AB}  - 3\overrightarrow {AC}  + 3\overrightarrow {AB}  = \overrightarrow 0$ $\Leftrightarrow \overrightarrow {AM}  = \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {AC}$.

Gọi $M$ là trung điểm $BC$.

Ta có $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB}  - \overrightarrow {AC} } \right|$ $\Leftrightarrow \left| {2\overrightarrow {AM} } \right| = \left| {\overrightarrow {CB} } \right| \Leftrightarrow AM = \dfrac{1}{2}BC$.

Trung tuyến kẻ từ $A$ bằng một nửa cạnh $BC$ nên tam giác $ABC$ vuông tại $A$.

Gọi $H$ là chân đường cao kẻ từ $A$ của tam giác $ABC$.

Theo đề ta có: ${S_{ABN}} = 3{S_{ACN}}$ $\Leftrightarrow \dfrac{1}{2}AH.BN = \dfrac{3}{2}AH.CN$ $\Leftrightarrow BN = 3CN$

$\Leftrightarrow \overrightarrow {BN}  =  - 3\overrightarrow {CN}  \Leftrightarrow \overrightarrow {BN}  =  - 3\left( {\overrightarrow {BN}  - \overrightarrow {BC} } \right) \Leftrightarrow 4\overrightarrow {BN}  = 3\overrightarrow {BC} \;\left( * \right)$.

Ta có $\overrightarrow {BN}  = \left( {{x_N} - 2;{y_N} - 3} \right)$; $\overrightarrow {BC}  = \left( { - 3; - 5} \right)$.

Do đó $\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}4\left( {{x_N} - 2} \right) = 3\left( { - 3} \right)\\4\left( {{y_N} - 3} \right) = 3\left( { - 5} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} =  - \dfrac{1}{4}\\{y_N} =  - \dfrac{3}{4}\end{array} \right.$. Vậy $N\left( { - \dfrac{1}{4}; - \dfrac{3}{4}} \right)$.

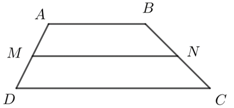
Ta có $M,\,N$ là trung điểm của $AD$ và $BC$ nên $\overrightarrow {MD}  + \overrightarrow {MA}  = \overrightarrow 0$ và $\overrightarrow {BN}  + \overrightarrow {CN}  = \overrightarrow 0$.

Khi đó: $\left| {\overrightarrow {MN}  + \overrightarrow {BD}  + \overrightarrow {CA} } \right| = \left| {\overrightarrow {MN}  + \overrightarrow {BN}  + \overrightarrow {NM}  + \overrightarrow {MD}  + \overrightarrow {CN}  + \overrightarrow {NM}  + \overrightarrow {MA} } \right|$

$= \left| {\overrightarrow {MN}  + 2\overrightarrow {NM} } \right| = \left| {\overrightarrow {NM} } \right| = NM = \dfrac{1}{2}\left( {AB + CD} \right) = \dfrac{{3a}}{2}$.

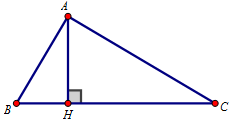
Ta có $A{B^2} = BH.BC$ và $A{C^2} = CH.CB$. Do đó: $\dfrac{{CH}}{{BH}} = \dfrac{{A{C^2}}}{{A{B^2}}} = \dfrac{{16}}{9}$ $\Rightarrow HC = \dfrac{{16}}{9}.HB$.

Mà $\overrightarrow {HC} ,\overrightarrow {HB}$ ngược hướng nên $\overrightarrow {HC}  =  - \dfrac{{16}}{9}\overrightarrow {HB}$.

Khi đó, gọi $H\left( {x;y} \right)$ thì $\overrightarrow {HC}  = \left( {1 - x\,;2 - y} \right)$, $\overrightarrow {HB}  = \left( {1 - x\,; - 3 - y} \right)$.

Suy ra: $\left\{ \begin{array}{l}1 - x =  - \dfrac{{16}}{9}\left( {1 - x} \right)\\2 - y =  - \dfrac{{16}}{9}\left( { - 3 - y} \right)\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - \dfrac{6}{5}\end{array} \right.$ $\Leftrightarrow H\left( {1\,;\, - \dfrac{6}{5}} \right)$.

$P \in Oy \Rightarrow P\left( {0;{\rm{ }}y} \right)$.

$G \in Ox \Rightarrow G\left( {x;{\rm{ 0}}} \right)$.

Điểm $G$ là trọng tâm của tam giác $MNP$ $\Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{1 + 5 + 0}}{3}\\0 = \dfrac{{\left( { - 1} \right) + \left( { - 3} \right) + y}}{3}\end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 4\end{array} \right.$

$\Rightarrow P\left( {0;4} \right),G\left( {2;0} \right)$

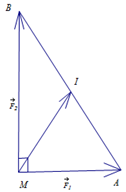
Cường độ lực tổng hợp của $\left| {\overrightarrow F } \right| = \left| {\overrightarrow {{F_1}}  + {{\overrightarrow F }_2}} \right|$$= \left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right|$$= 2\left| {\overrightarrow {MI} } \right| = AB$ ($I$ là trung điểm của $AB$). Ta có $AB = \sqrt {M{A^2} + M{B^2}}  = 500$ suy ra $\left| {\overrightarrow F } \right| = 500\,\left( N \right)$.

Ta có

$\begin{array}{l}\overrightarrow {BM}  = \overrightarrow {BC}  - 2\overrightarrow {AB}  \Leftrightarrow \overrightarrow {AM} \,\, = \overrightarrow {BC} \, - \overrightarrow {AB}  \Leftrightarrow \overrightarrow {AM}  =  - \overrightarrow {AC}  + 2\overrightarrow {BC} \\\overrightarrow {CN}  = x\overrightarrow {AC}  - \overrightarrow {BC} . \Leftrightarrow \overrightarrow {CA}  + \overrightarrow {AN}  = x\overrightarrow {AC}  - \overrightarrow {BC}  \Leftrightarrow \overrightarrow {AN}  = \left( {x + 1} \right)\overrightarrow {AC}  - \overrightarrow {BC} \end{array}$

Để $A,{\rm{ }}M,{\rm{ }}N$ thẳng hàng thì $\exists k \ne 0$ sao cho $\overrightarrow {AM}  = k\overrightarrow {AN}$

Hay  $\left( {x + 1} \right)\overrightarrow {AC}  - \overrightarrow {BC}  = k\left( { - \overrightarrow {AC}  + 2\overrightarrow {BC} } \right) \Leftrightarrow \left\{ \begin{array}{l}x + 1 =  - k\\ - 1 = 2k\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \dfrac{{ - 1}}{2}\\x = \dfrac{{ - 1}}{2}\end{array} \right.$

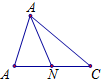
Gọi $I$ là điểm thỏa mãn $\overrightarrow {IA}  + 3\overrightarrow {IB}  - 2\overrightarrow {IC}  = \overrightarrow 0$.

$\left| {\overrightarrow {MA}  + 3\overrightarrow {MB}  - 2\overrightarrow {MC} } \right| = \left| {2\overrightarrow {MA}  - \overrightarrow {MB}  - \overrightarrow {MC} } \right|$$\Leftrightarrow \left| {2\overrightarrow {MI}  + \overrightarrow {IA}  + 3\overrightarrow {IB}  - 2\overrightarrow {IC} } \right| = \left| {\overrightarrow {BA}  + \overrightarrow {CA} } \right|$ $\left( 1 \right)$.

Gọi $N$ là trung điểm $BC$. Ta được: $\left( 1 \right) \Leftrightarrow 2\left| {\overrightarrow {MI} } \right| = 2\left| { - \overrightarrow {AN} } \right| \Leftrightarrow IM = AN$.

$I$, $A$, $N$ cố định nên tập hợp các điểm $M$ là đường tròn tâm $I$, bán kính $AN$.

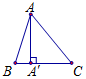
$\overrightarrow u  = \left( {\tan B} \right)\overrightarrow {A'B}  + \left( {\tan C} \right) \overrightarrow {A'C}$ $\Leftrightarrow \overrightarrow u  = \dfrac{{AA'}}{{BA'}}\overrightarrow {A'B}  + \dfrac{{AA'}}{{CA'}}\overrightarrow {A'C}$.

Ta thấy hai vecto $\dfrac{{AA'}}{{BA'}}\overrightarrow {A'B}$ và $\dfrac{{AA'}}{{CA'}}\overrightarrow {A'C}$ ngược hướng và độ dài mỗi vecto bằng $AA'$ nên chúng là hai vecto đối nhau.

Vậy $\overrightarrow u  = \overrightarrow 0$.