Trong mặt phẳng tọa độ $Oxy$, cho hình bình hành $ABCD$ có $A\left( {2;{\rm{ }}3} \right)$ và tâm $I\left( { - 1;{\rm{ }}1} \right)$. Biết điểm $M\left( {4;{\rm{ }}9} \right)$ nằm trên đường thẳng $AD$ và điểm $D$ có tung độ gấp đôi hoành độ. Tìm các đỉnh còn lại của hình bình hành?
Trả lời bởi giáo viên
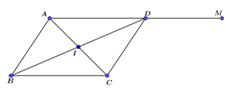
Ta có $I$ là trung điểm của $AC$ $ \Rightarrow C\left( { - 4;{\rm{ }} - 1} \right)$.
Điểm $D$ có tung độ gấp đôi hoành độ $ \Rightarrow D\left( {{x_D};2{x_D}} \right)$.
Lại có $\overrightarrow {AM} = \left( {2;{\rm{ }}6} \right)$, $\overrightarrow {AD} = \left( {{x_D} - 2;{\rm{ }}2{x_D} - 3} \right)$.
Mà $A$, $M$, $D$ thẳng hàng $ \Rightarrow 6\left( {{x_D} - 2} \right) = 2\left( {2{x_D} - 3} \right)$ $ \Leftrightarrow {x_D} = 3$ $ \Rightarrow D\left( {3;{\rm{ }}6} \right)$.
$I$ là trung điểm $BD$ $ \Rightarrow B\left( { - 5;{\rm{ }} - 4} \right)$.
Hướng dẫn giải:
- Tìm tọa độ \(C\) với chú ý \(I\) là trung điểm của \(AC\)
- Tìm \(D\) chú ý \(\overrightarrow {AD} ,\overrightarrow {AM} \) cùng phương.

