Cho tứ giác \(ABCD\) trên cạnh \(AB\), \(CD\) lần lượt lấy các điểm \(M\), \(N\) sao cho \(3\overrightarrow {AM} = 2\overrightarrow {AB} \) và \(3\overrightarrow {DN} = 2\overrightarrow {DC} \). Tính vectơ \(\overrightarrow {MN} \) theo hai vectơ \(\overrightarrow {AD} \), \(\overrightarrow {BC} \).
Trả lời bởi giáo viên
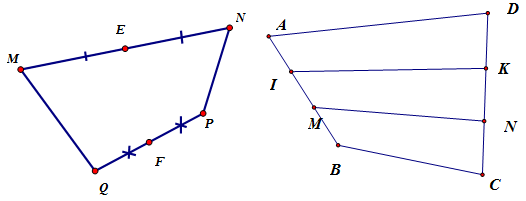
Bước 1:
Ta chứng minh bài toán sau:
Gọi \(E\), \(F\) lần lượt là trung điểm của \(MN\), \(PQ\) thì ta có: \(\overrightarrow {EF} = \dfrac{1}{2}\left( {\overrightarrow {MQ} + \overrightarrow {NP} } \right)\).
Thật vậy, ta có: $\overrightarrow {EF} = \dfrac{1}{2}\left( {\overrightarrow {EP} + \overrightarrow {EQ} } \right)$\( = \dfrac{1}{2}\left( {\overrightarrow {EN} + \overrightarrow {NP} + \overrightarrow {EM} + \overrightarrow {MQ} } \right)\)\( = \dfrac{1}{2}\left( {\overrightarrow {MQ} + \overrightarrow {NP} } \right)\)
Bước 2:
Gọi \(I\), \(K\) lần lượt là trung điểm của \(AM\) và \(DN\).
\( \Rightarrow \overrightarrow {IK} = \dfrac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {MN} } \right)\)
Bước 3:
Khi đó M là trung điểm của IB và N là trung điểm của KC.
Áp dụng kết quả của bài toán trên ta có: \(\overrightarrow {MN} = \dfrac{1}{2}\left( {\overrightarrow {BC} + \overrightarrow {IK} } \right)\)\( = \dfrac{1}{2}\left( {\overrightarrow {BC} + \dfrac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {MN} } \right)} \right)\)
\( = \dfrac{1}{2}\left( {\overrightarrow {BC} + \dfrac{1}{2}\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {MN} } \right)\)\( = \dfrac{1}{2}\overrightarrow {BC} + \dfrac{1}{4}\overrightarrow {AD} + \dfrac{1}{4}\overrightarrow {MN} \)
\( \Rightarrow \dfrac{3}{4}\overrightarrow {MN} = \dfrac{1}{2}\overrightarrow {BC} + \dfrac{1}{4}\overrightarrow {AD} \)
\( \Rightarrow \overrightarrow {MN} = \dfrac{1}{3}\overrightarrow {AD} + \dfrac{2}{3}\overrightarrow {BC} \).
Hướng dẫn giải:
Bước 1:
Chứng minh: Cho tứ giác MNPQ, nếu \(E\), \(F\) lần lượt là trung điểm của \(MN\), \(PQ\) thì ta có: \(\overrightarrow {EF} = \dfrac{1}{2}\left( {\overrightarrow {MQ} + \overrightarrow {NP} } \right)\)
Bước 2: Gọi \(I\), \(K\) lần lượt là trung điểm của \(AM\) và \(DN\). Biểu diễn \(\overrightarrow {IK} \) theo \(\overrightarrow {AD} \) và \(\overrightarrow {MN} \)
Bước 3: Biểu diễn \(\overrightarrow {MN} \) theo \(\overrightarrow {BC} \) và \(\overrightarrow {IK} \) và biến đổi để xuất hiện hai vectơ \(\overrightarrow {AD} \), \(\overrightarrow {BC} \).

