Cho \(\Delta ABC\). Gọi \(M\), \(N\) là các điểm thỏa mãn: \(\overrightarrow {MA\,}  + \overrightarrow {MB\,}  = \overrightarrow {0\,} \), \(2\overrightarrow {NA\,}  + 3\overrightarrow {NC}  = \overrightarrow {0\,} \) và \(\overrightarrow {BC\,}  = k\overrightarrow {BP\,} \). Tìm \(k\) để ba điểm \(M\), \(N\), \(P\) thẳng hàng.

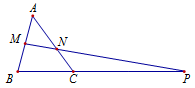
Cách 1: Tự luận:

Ta có   \(\overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM}  = \dfrac{3}{5}\overrightarrow {AC}  - \dfrac{1}{2}\overrightarrow {AB} \)\(\left( 1 \right)\)

            \(\overrightarrow {NP}  = \overrightarrow {NC}  + \overrightarrow {CP}  = \dfrac{2}{5}\overrightarrow {AC}  + \left( {\overrightarrow {BP}  - \overrightarrow {BC} } \right)\)

                   \( = \dfrac{2}{5}\overrightarrow {AC}  + \left( {\dfrac{1}{k} - 1} \right)\overrightarrow {BC} \)

                   \( = \dfrac{2}{5}\overrightarrow {AC}  + \left( {\dfrac{1}{k} - 1} \right)\left( {\overrightarrow {AC}  - \overrightarrow {AB} } \right)\)

                   \( = \left( {\dfrac{1}{k} - \dfrac{2}{5}} \right)\overrightarrow {AC}  - \left( {\dfrac{1}{k} - 1} \right)\overrightarrow {AB} \)

Để ba điểm \(M\), \(N\), \(P\) thẳng hàng thì $\exists m \in \mathbb{R}:\overrightarrow {NP}  = m\overrightarrow {MN} $

\( \Leftrightarrow \left( {\dfrac{1}{k} - \dfrac{3}{5}} \right)\overrightarrow {AC}  - \left( {\dfrac{1}{k} - 1} \right)\overrightarrow {AB}  = \dfrac{{3m}}{5}\overrightarrow {AC}  - \dfrac{m}{2}\overrightarrow {AB} \)

Điều kiện: \(\left\{ \begin{array}{l}\dfrac{1}{k} - \dfrac{3}{5} = \dfrac{{3m}}{5}\\ - \left( {\dfrac{1}{k} - 1} \right) =  - \dfrac{m}{2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m = 4\\k = \dfrac{1}{3}\end{array} \right.\).

Vậy \(k = \dfrac{1}{3}\).

Cách 2: Trắc nghiệm:

Ta có   \(\overrightarrow {MA\,}  + \overrightarrow {MB\,}  = \overrightarrow {0\,}  \Leftrightarrow \overrightarrow {MA\,}  =  - \overrightarrow {MB\,}  \Rightarrow \dfrac{{\overline {MA} }}{{\overline {MB} }} =  - 1\)

\(\overrightarrow {BC\,}  = k\overrightarrow {BP\,}  \Leftrightarrow \overrightarrow {PB\,}  = \left( {1 - k} \right)\overrightarrow {PC\,}  \Rightarrow \dfrac{{\overline {PB} }}{{\overline {PC} }} = 1 - k\)

            \(2\overrightarrow {NA\,}  + 3\overrightarrow {NC}  = \overrightarrow {0\,}  \Leftrightarrow 2\overrightarrow {NA\,}  =  - \dfrac{3}{2}\overrightarrow {NC\,}  \Rightarrow \dfrac{{\overline {NA} }}{{\overline {NC} }} =  - \dfrac{3}{2}\)

Theo định lí Mêlêxauýt ba điểm \(M\), \(N\), \(P\) thẳng hàng khi

\(\dfrac{{\overline {MA} }}{{\overline {MB} }} \cdot \dfrac{{\overline {PB} }}{{\overline {PC} }} \cdot \dfrac{{\overline {NC} }}{{\overline {NA} }} = 1\)\( \Leftrightarrow \left( { - 1} \right).\left( {1 - k} \right).\left( { - \dfrac{3}{2}} \right) = 1 \Leftrightarrow k = \dfrac{1}{3}\).

Vậy \(k = \dfrac{1}{3}\).