Cho tam giác đều ABC cạnh a có G là trọng tâm. Độ dài của vec tơ \(\overrightarrow {AC} - \overrightarrow {BG} \) là
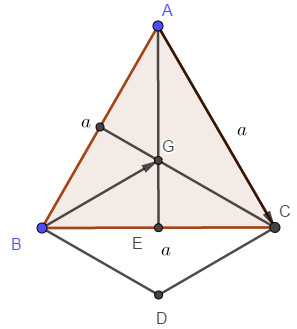
Ta có G là trọng tâm tam giác ABC nên \(GB \bot AC\) và \(GB = \dfrac{{a\sqrt 3 }}{3}\).
Vẽ hình bình hành \(BGCD\). Khi đó \(\overrightarrow {BG} = \overrightarrow {DC} \)\( \Rightarrow CD = \dfrac{{a\sqrt 3 }}{3}\)
\(\overrightarrow {AC} - \overrightarrow {BG} = \overrightarrow {AC} + \overrightarrow {CD} = \overrightarrow {AD} \)\( \Rightarrow \left| {\overrightarrow {AC} - \overrightarrow {BG} } \right| = AD\)
Vì \(GB \bot AC\) nên \(AC \bot CD\). Suy ra \(AD = \sqrt {{a^2} + \dfrac{{{a^2}}}{3}} = \dfrac{{2a\sqrt 3 }}{3}\).
Vậy \(\left| {\overrightarrow {AC} - \overrightarrow {BG} } \right| = \dfrac{{2a\sqrt 3 }}{3}\).
Cho tam giác ABC. E là điểm trên đoạn AB sao cho \(\overrightarrow {AE} = \dfrac{1}{4}\overrightarrow {AB} \). N là trung điểm của AC. Tập hợp điểm M thỏa mãn\(\overrightarrow {MA} - \dfrac{1}{2}\overrightarrow {AB} + \overrightarrow {MC} = \overrightarrow 0 \). Khi đó

N là trung điểm của AC nên \(\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MN} \).
Ta có:
\(\begin{array}{l}\overrightarrow {MA} - \dfrac{1}{2}\overrightarrow {AB} + \overrightarrow {MC} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MC} = \dfrac{1}{2}\overrightarrow {AB} \\ \Leftrightarrow \overrightarrow {MN} = \dfrac{1}{4}\overrightarrow {AB} = \overrightarrow {AE} \end{array}\)
Khi đó M là điểm thỏa mãn AENM là hình bình hành.
Cho ba điểm phân biệt \(A,\;B,\;C\). Đẳng thức nào sau đây đúng?
Xét các đáp án:
Đáp án A. Ta có \(\overrightarrow {CA} - \overrightarrow {BA} = \overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {CB} = - \overrightarrow {BC} \).Vậy A sai.
Đáp án B. Ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \ne \overrightarrow {BC} \) (với \(D\) là điểm thỏa mãn \(ABDC\) là hình bình hành). Vậy B sai.
Đáp án C. Ta có \(\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {CA} + \overrightarrow {AB} = \overrightarrow {CB} \). Vậy C đúng.
Gọi \(O\) là tâm hình bình hành \(ABCD\). Đẳng thức nào sau đây sai?
Xét các đáp án:
Đáp án A. Ta có \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {BA} = \overrightarrow {CD} \). Vậy A đúng.
Đáp án B. Ta có \(\left\{ \begin{array}{l}\overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {CB} = - \overrightarrow {AD} \\\overrightarrow {OD} - \overrightarrow {OA} = \overrightarrow {AD} \end{array} \right.\). Vậy B sai.
Đáp án C. Ta có \(\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} .\) Vậy C đúng.
Đáp án D. Ta có \(\left\{ \begin{array}{l}\overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {AC} \\\overrightarrow {DC} - \overrightarrow {DA} = \overrightarrow {AC} \end{array} \right.\). Vậy D đúng.
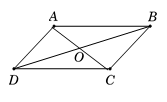
Điều kiện nào là điều kiện cần và đủ để \(I\) là trung điểm của đoạn thẳng \(AB\)?
Điều kiện cần và đủ để \(I\) là trung điểm của đoạn thẳng \(AB\) là \(\overrightarrow {IA} = - \overrightarrow {IB} \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \)
Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(\left| {\overrightarrow {AB} - \overrightarrow {DA} } \right|.\)
Ta có \(\left| {\overrightarrow {AB} - \overrightarrow {DA} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\sqrt 2 .\)
Cho \(\overrightarrow {AB} = - \overrightarrow {CD} \). Khẳng định nào sau đây đúng?
Ta có \(\overrightarrow {AB} = - \overrightarrow {CD} = \overrightarrow {DC} \). Do đó:
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ngược hướng.
\(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng độ dài.
\(ABCD\) là hình bình hành nếu \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) không cùng giá.
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 .\)
Cho tam giác đều \(ABC\) cạnh \(a,\) \(H\) là trung điểm của \(BC\). Tính \(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right|.\)
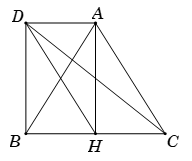
Gọi \(D\) là điểm thỏa mãn tứ giác \(ACHD\) là hình bình hành \(\Rightarrow CH = AD \Rightarrow AD = HB\).
\( \Rightarrow AHBD\) là hình chữ nhật \( \Rightarrow BD = AH\).
\(\left| {\overrightarrow {CA} - \overrightarrow {HC} } \right| = \left| {\overrightarrow {CA} + \overrightarrow {CH} } \right| = \left| {\overrightarrow {CD} } \right| = CD.\)
Ta có \(CD = \sqrt {B{D^2} + B{C^2}} = \sqrt {A{H^2} + B{C^2}} \)\( = \sqrt {\dfrac{{3{a^2}}}{4} + {a^2}} = \dfrac{{a\sqrt 7 }}{2}\)
Cho tam giác \(ABC\) vuông cân đỉnh \(A\), đường cao \(AH\). Khẳng định nào sau đây sai?
Do \(\Delta ABC\) cân tại \(A\), \(AH\) là đường cao nên \(H\) là trung điểm \(BC\).
Xét các đáp án:
Đáp án A. Ta có \(\left\{ \begin{array}{l}\left| {\overrightarrow {AH} + \overrightarrow {HB} } \right| = \left| {\overrightarrow {AB} } \right| = a\\\left| {\overrightarrow {AH} + \overrightarrow {HC} } \right| = \left| {\overrightarrow {AC} } \right| = a\end{array} \right.\)
\( \Rightarrow \left| {\overrightarrow {AH} + \overrightarrow {HB} } \right| = \left| {\overrightarrow {AH} + \overrightarrow {HC} } \right|.\)
Đáp án B. Ta có \(\left\{ \begin{array}{l}\overrightarrow {AH} - \overrightarrow {AB} = \overrightarrow {BH} \\\overrightarrow {AH} - \overrightarrow {AC} = \overrightarrow {CH} = - \overrightarrow {BH} \end{array} \right..\) Do đó B sai.
Đáp án C. Ta có \(\left\{ \begin{array}{l}\overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {AC} \\\overrightarrow {HC} - \overrightarrow {HA} = \overrightarrow {AC} \end{array} \right.\)\( \Rightarrow \overrightarrow {BC} - \overrightarrow {BA} = \overrightarrow {HC} - \overrightarrow {HA} \)
Đáp án D. Ta có \(\left| {\overrightarrow {AB} - \overrightarrow {AH} } \right| = \left| {\overrightarrow {HB} } \right| = \left| {\overrightarrow {AH} } \right|\) (do \(\Delta ABC\) vuông cân tại \(A\)).

Cho hình bình hành \(ABCD\). Đẳng thức nào sau đây đúng?
Do \(ABCD\) là hình bình hành nên \(\overrightarrow {BC} = \overrightarrow {AD} .\)
Suy ra \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} .\)
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Hỏi vectơ \(\overrightarrow {AO} - \overrightarrow {DO} \) bằng vectơ nào trong các vectơ sau?
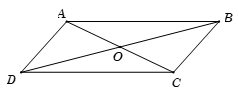
Ta có \(\overrightarrow {AO} - \overrightarrow {DO} = - \overrightarrow {OA} + \overrightarrow {OD} = \overrightarrow {OD} - \overrightarrow {OA} = \overrightarrow {AD} = \overrightarrow {BC} \)
Gọi \(O\) là tâm của hình vuông \(ABCD\). Vectơ nào trong các vectơ dưới đây bằng \(\overrightarrow {CA} ?\)
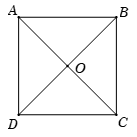
Xét các đáp án:
Đáp án A. Ta có \(\overrightarrow {BC} + \overrightarrow {AB} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} = - \overrightarrow {CA} .\)
Đáp án B. Ta có \( - \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OC} - \overrightarrow {OA} = \overrightarrow {AC} = - \overrightarrow {CA} .\)
Đáp án C. Ta có \(\overrightarrow {BA} + \overrightarrow {DA} = - \left( {\overrightarrow {AD} + \overrightarrow {AB} } \right) = - \overrightarrow {AC} = \overrightarrow {CA} .\)
Đáp án D. Ta có \(\overrightarrow {DC} - \overrightarrow {CB} = \overrightarrow {DC} + \overrightarrow {BC} = - \left( {\overrightarrow {CD} + \overrightarrow {CB} } \right) = - \overrightarrow {CA} .\)
Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Gọi \(E,\;F\) lần lượt là trung điểm của \(AB,\;BC\). Đẳng thức nào sau đây sai?
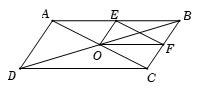
Ta có \(OF,\;OE\) lần lượt là đường trung bình của tam giác \(\Delta BCD\) và \(\Delta ABC\).
\( \Rightarrow BEOF\) là hình bình hành.
\(\overrightarrow {BE} + \overrightarrow {BF} = \overrightarrow {BO} \)\( \Rightarrow \overrightarrow {BE} + \overrightarrow {BF} - \overrightarrow {DO} = \overrightarrow {BO} - \overrightarrow {DO} \) \( = \overrightarrow {OD} - \overrightarrow {OB} = \overrightarrow {BD} \)
Cho tam giác \(ABC.\) Tập hợp tất cả các điểm \(M\) thỏa mãn đẳng thức \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right|\) là
Ta có \(\left| {\overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} - \overrightarrow {BA} } \right| \Leftrightarrow \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AM} } \right| \Rightarrow AM = BC\)
Mà \(A,\;B,\;C\) cố định \( \Rightarrow \) Tập hợp điểm \(M\) là đường tròn tâm \(A\), bán kính \(BC\).
Cho hình bình hành \(ABCD\). Tập hợp tất cả các điểm \(M\) thỏa mãn đẳng thức \(\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} \) là
\(\overrightarrow {MA} + \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} \) \(\Leftrightarrow \overrightarrow {MB} - \overrightarrow {MC} = \overrightarrow {MD} - \overrightarrow {MA} \)
\( \Leftrightarrow \overrightarrow {CB} = \overrightarrow {AD} \): vô lí
\( \Rightarrow \) Không có điểm \(M\) thỏa mãn.
Cho hình chữ nhật \(ABCD.\) Khẳng định nào sau đây đúng?
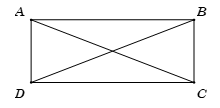
Ta có \(\left\{ \begin{array}{l}\left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = BD\\\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\end{array} \right..\)
$BD = AC \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right|.$
Cho 3 điểm$A,{\rm{ }}B,{\rm{ }}C$. Đẳng thức nào sau đây đúng.
Ta có: $\overrightarrow {AB} = \overrightarrow {CB} - \overrightarrow {CA} $ (qui tắc 3 điểm).
Cho $4$ điểm bất kì $A,B,C,O$. Đẳng thức nào sau đây đúng?
Theo qui tắc $3$ điểm ta có: $\overrightarrow {OA} = \overrightarrow {CA} - \overrightarrow {CO} $.
Chọn khẳng định sai:
Ta có: $\overrightarrow {IA} - \overrightarrow {IB} = \overrightarrow {BA} \ne \overrightarrow 0 $ nên A sai.
Cho hình vuông $ABCD$ cạnh $a$, tâm $O$. Khi đó: $\left| {\overrightarrow {OA} - \overrightarrow {BO} } \right| = $
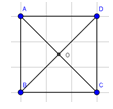
Ta có: $\left| {\overrightarrow {OA} - \overrightarrow {BO} } \right| = \left| {\overrightarrow {CO} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {CB} } \right| = a$.

