Cho ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c $ đều khác vectơ – không. Trong đó hai vectơ $\overrightarrow a ,\overrightarrow b $ cùng hướng, hai vectơ $\overrightarrow a \,,{\rm{ }}\overrightarrow c $ đối nhau. Khẳng định nào sau đây đúng ?
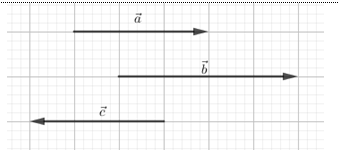
Quan sát hình vẽ trên ta thấy hai vectơ $\overrightarrow b ,\overrightarrow c $ ngược hướng.
Cho các điểm phân biệt $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D,{\rm{ }}E,{\rm{ }}F$. Đẳng thức nào sau đây sai ?
Ta có: $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = \overrightarrow {AF} + \overrightarrow {ED} + \overrightarrow {BC} $
$\begin{array}{l} \Leftrightarrow \overrightarrow {AB} - \overrightarrow {AF} + \overrightarrow {CD} - \overrightarrow {BC} + \overrightarrow {EF} - \overrightarrow {ED} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {FB} + \overrightarrow {DF} + \overrightarrow {CD} + \overrightarrow {CB} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {DB} + \overrightarrow {CD} + \overrightarrow {CB} = \overrightarrow 0 \end{array}$
$ \Leftrightarrow \overrightarrow {CB} + \overrightarrow {CB} = \overrightarrow 0 $
\( \Leftrightarrow 2\overrightarrow {CB} = \overrightarrow 0 \) (vô lý) nên A sai.
Tương tự với các đáp án B, C, D ta sẽ thấy các đáp án đó đều đúng.
Gọi $G$ là trọng tâm tam giác vuông $ABC\;$ với cạnh huyền $BC = 12$. Vectơ $\overrightarrow {GB} - \overrightarrow {CG} $ có độ dài bằng bao nhiêu?
Ta có: $\overrightarrow {GB} - \overrightarrow {CG} = \overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GE} = \dfrac{2}{3}\overrightarrow {AE} $ (Vì \(\overrightarrow {GE} = \dfrac{1}{3}\overrightarrow {AE} \)).
$ \Rightarrow \left| {\overrightarrow {GB} - \overrightarrow {CG} } \right| = \dfrac{2}{3}\left| {\overrightarrow {AE} } \right| = \dfrac{2}{3}.\dfrac{{BC}}{2} = \dfrac{{BC}}{3} = 4$
Cho tam giác đều $ABC$ cạnh \(a\), gọi $G$ là trọng tâm. Khi đó giá trị $\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right|$ là:
Ta có:
$\left| {\overrightarrow {AB} - \overrightarrow {GC} } \right| = \left| {\overrightarrow {AC} + \overrightarrow {CB} + \overrightarrow {CG} } \right| = \left| {\overrightarrow {AG} + \overrightarrow {CB} } \right| = \left| {2\overrightarrow {GH} + 2\overrightarrow {HB} } \right|$
$ = 2\left| {\overrightarrow {GH} + \overrightarrow {HB} } \right| = 2\left| {\overrightarrow {GB} } \right| = 2GB = 2GA = 2.\dfrac{2}{3}AH = \dfrac{4}{3} .\dfrac{a\sqrt 3}{2}= \dfrac{{2a\sqrt 3 }}{3}$.
Chỉ ra vectơ tổng \(\overrightarrow {MN} - \overrightarrow {QP} + \overrightarrow {RN} - \overrightarrow {PN} + \overrightarrow {QR} \) trong các vectơ sau:
Ta có: \(\overrightarrow {MN} + \overrightarrow {NP} + \overrightarrow {PQ} + \overrightarrow {QR} + \overrightarrow {RN} = \overrightarrow {MN} \).
Cho bốn điểm $A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D$ phân biệt. Khi đó vectơ \(\overrightarrow u = \overrightarrow {AD} - \overrightarrow {CD} + \overrightarrow {CB} - \overrightarrow {AB} \) bằng:
Ta có: \(\overrightarrow u = \overrightarrow {AD} - \overrightarrow {CD} + \overrightarrow {CB} - \overrightarrow {AB} = \overrightarrow {AD} - \overrightarrow {AB} + \overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {BD} + \overrightarrow {DB} = \overrightarrow 0 \)
Gọi $B$ là trung điểm của đoạn thẳng $AC$. Đẳng thức nào sau đây là đúng?
Ta có: \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow 0 \).
Cho tam giác \(ABC\), trọng tâm là \(G\). Phát biểu nào là đúng?
Ta có: $\left| {\overrightarrow {GA} - \overrightarrow {BG} - \overrightarrow {CG} } \right| = \left| {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right| = \left| {\overrightarrow 0 } \right| = 0$.
Cho tam giác \(ABC\). Để điểm \(M\) thoả mãn điều kiện \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) thì \(M\) phải thỏa mãn mệnh đề nào?
Ta có: \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
Vậy: \(M\) là điểm sao cho tứ giác \(BAMC\)là hình bình hành.
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} ,\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) đều bằng \(100N\) và $\widehat {AMB} = {60^0}$. Khi đó cường độ lực của $\overrightarrow {{F_3}} $ là:
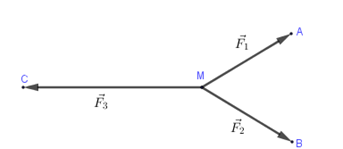
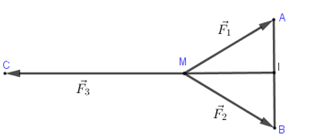
Vật \(M\) đứng yên \( \Leftrightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow 0 \)
Hay \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
Gọi \(I\) là trung điểm của \(AB\) \( \Rightarrow 2\overrightarrow {MI} + \overrightarrow {MC} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {MC} = - 2\overrightarrow {MI} \Rightarrow MC = 2MI\)
Gọi \(I\) là trung điểm của \(AB.\)
Vì \(MAB\) là tam giác đều nên \(MI = MA.\dfrac{{\sqrt 3 }}{2} = 50\sqrt 3 .\)
Vậy \(MC = 2MI = 100\sqrt 3 N\)
Vậy: \(\overrightarrow {{F_3}} \) có cường độ \(100\sqrt 3 \,N\).
Cho lục giác đều $ABCDEF$ và $O$ là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?
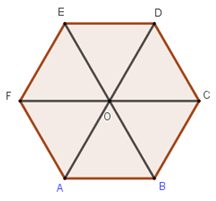
Ta có:
$\begin{array}{l}
\overrightarrow {OA} + \overrightarrow {OC} - \overrightarrow {EO} = \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow 0 \\
\Rightarrow A\,\,\text{đúng}\\
\overrightarrow {BC} - \overrightarrow {EF} = \overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AO} + \overrightarrow {OD} = \overrightarrow {AD} \\
\Rightarrow B\,\,\text{đúng}\\
\overrightarrow {OA} - \overrightarrow {OE} = \overrightarrow {EA} \\
\overrightarrow {EB} - \overrightarrow {OC} = \overrightarrow {EB} + \overrightarrow {CO} = \overrightarrow {EB} + \overrightarrow {BA} = \overrightarrow {EA} \\
\Rightarrow \overrightarrow {OA} - \overrightarrow {OE} = \overrightarrow {EB} - \overrightarrow {OC} \\
\Rightarrow C\,\,\text{đúng}
\end{array}$
$\overrightarrow {AB} + \overrightarrow {CD} - \overrightarrow {EF} = \overrightarrow {AB} + \overrightarrow {BO} - \overrightarrow {OA} $
$ = \overrightarrow {AO} - \overrightarrow {OA} = 2\overrightarrow {AO} \ne \overrightarrow 0 $
Hay D sai.
