Tổng của hai véc tơ

$\begin{array}{l}\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM} \\\overrightarrow {AM}  = \overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {BC} \\\overrightarrow {AM}  = \overrightarrow {AB}  + \dfrac{3}{4}\left( {\overrightarrow {BA}  + \overrightarrow {AC} } \right)\\\overrightarrow {AM}  = \overrightarrow {AB}  - \dfrac{3}{4}\overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {AC} \\\overrightarrow {AM}  = \dfrac{1}{4}\overrightarrow {AB}  + \dfrac{3}{4}\overrightarrow {AC} \end{array}$

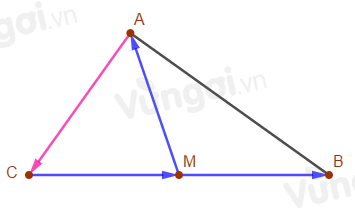
Ta có M là trung điểm của BC nên $\overrightarrow {CM}  = \overrightarrow {MB}$

Suy ra

$\begin{array}{l}\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {AC}  = \overrightarrow {MA}  + \overrightarrow {CM}  + \overrightarrow {AC} \\ = \overrightarrow {CA}  + \overrightarrow {AC}  = \overrightarrow 0 \end{array}$

Xét các đáp án:

+) Đáp án A. Ta có $\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {AD}  \ne \overrightarrow {BC}$ (với $D$ là điểm thỏa mãn $ABDC$ là hình bình hành). Vậy A sai.

+) Đáp án B. Ta có $\overrightarrow {MP}  + \overrightarrow {NM}  = \overrightarrow {NM}  + \overrightarrow {MP}  = \overrightarrow {NP}$. Vậy B đúng.

+) Đáp án C. Ta có $\overrightarrow {CA}  + \overrightarrow {BA}  =  - \left( {\overrightarrow {AC}  + \overrightarrow {AB} } \right) =  - \overrightarrow {AD}  \ne \overrightarrow {CB}$ (với $D$ là điểm thỏa mãn $ABDC$ là hình bình hành). Vậy C sai.

+) Đáp án D. Ta có $\overrightarrow {AA}  + \overrightarrow {BB}  = \overrightarrow 0  + \overrightarrow 0  = \overrightarrow 0  \ne \overrightarrow {AB}$. Vậy D sai.

Với ba điểm phân biệt $A,\;B,\;C$ nằm trên một đường thẳng, đẳng thức $\left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right|$ $\Leftrightarrow AB + BC = AC$ xảy ra khi $B$ nằm giữa $A$ và $C$.

Điểm $G$ là trọng tâm tam giác $ABC$ $\Leftrightarrow \overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$.

Với mỗi điểm $M$ bất kì và $I$ là trung điểm của đoạn thẳng $AB$ thì $\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI}$ hay $\overrightarrow {MI}  = \dfrac{1}{2}\left( {\overrightarrow {MA}  + \overrightarrow {MB} } \right).$

$I$ là trung điểm của $AB$ nếu $\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0$.

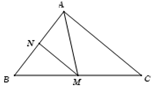
Xét các đáp án:

- Đáp án A. Ta có $\overrightarrow {AM}  + \overrightarrow {MB}  + \overrightarrow {BA}  = \overrightarrow 0$ (theo quy tắc ba điểm).

- Đáp án B, C. Ta có $\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MN}  = \overrightarrow {CA}$

(với điểm $N$ là trung điểm của $AB$).

- Đáp án D. Ta có $\overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM}$.

Gọi $M$ là trung điểm $BC$. Ta có $\Delta ABC$ vuông cân tại $A$ nên $AM = \dfrac{1}{2}BC.$ và $BC = a\sqrt 2$.

Ta có: $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = BC = a\sqrt 2 .$

Ta có $\left| {\overrightarrow {CA}  + \overrightarrow {AB} } \right| = \left| {\overrightarrow {CB} } \right| = CB$$= \sqrt {A{C^2} + A{B^2}}  = \sqrt {{3^2} + {4^2}}  = 5$

Gọi $M$ là trung điểm $BC \Rightarrow AM \bot BC.$

Trong tam giác vuông $AMB$, ta có $AM = AB.\sin \widehat {ABM} = a.\sin {30^0} = \dfrac{a}{2}.$

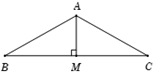
Ta có $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {2\overrightarrow {AM} } \right| = 2AM = a.$

Ta có $\overrightarrow {MN}  + \overrightarrow {PQ}  + \overrightarrow {RN}  + \overrightarrow {NP}  + \overrightarrow {QR}$$= \overrightarrow {MN}  + \overrightarrow {NP}  + \overrightarrow {PQ}  + \overrightarrow {QR}  + \overrightarrow {RN}$$= \overrightarrow {MN}$

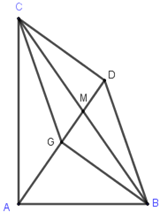
Dựng hình bình hành $GBDC$. Gọi $M$ là trung điểm $BC$.

Khi đó ta có $\left| {\overrightarrow {GB}  + \overrightarrow {GC} } \right| = \left| {\overrightarrow {GD} } \right| = GD = 2GM$$= \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{1}{2}BC = \dfrac{1}{3}BC = \dfrac{1}{3}.24 = 8$

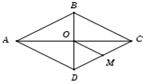
Gọi $O = AC \cap BD$ và $M$ là trung điểm của $CD$.

Ta có $\left| {\overrightarrow {AC}  + \overrightarrow {BD} } \right| = 2\left| {\overrightarrow {OC}  + \overrightarrow {OD} } \right| = 2\left| {2\overrightarrow {OM} } \right| = 4OM$

$= 4.\dfrac{1}{2}CD = 2\sqrt {O{D^2} + O{C^2}}  = 2\sqrt {\dfrac{{{a^2}}}{4} + {a^2}}  = a\sqrt 5 .$

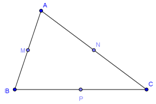
Vì $ANPM$là hình bình hành nên theo quy tắc hình bình hành ta có:$\overrightarrow {MP}  + \overrightarrow {MA}  = \overrightarrow {MN}$.

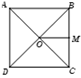
Gọi $M$ là trung điểm của $BC$.

Ta có $\left| {\overrightarrow {OB}  + \overrightarrow {OC} } \right| = 2\left| {\overrightarrow {OM} } \right| = 2OM = AB = a.$

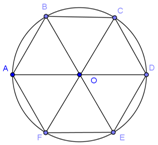
$\overrightarrow {AB}  + \overrightarrow {CD}  + \overrightarrow {EF}$$= \overrightarrow {AB}  + \overrightarrow {BO}  + \overrightarrow {OA}  = \overrightarrow 0  \ne \overrightarrow {AD}$ nên D sai.

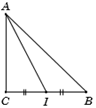
Ta có $AB = \sqrt 2  \Rightarrow AC = CB = 1.$

Gọi $I$ là trung điểm $BC$ $\Rightarrow AI = \sqrt {A{C^2} + C{I^2}}  = \dfrac{{\sqrt 5 }}{2}$

Khi đó: $\overrightarrow {AC}  + \overrightarrow {AB}  = 2\overrightarrow {AI}$$\Rightarrow \left| {\overrightarrow {AC}  + \overrightarrow {AB} } \right| = 2\left| {\overrightarrow {AI} } \right| = 2.\dfrac{{\sqrt 5 }}{2} = \sqrt 5$

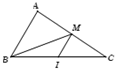
Gọi $I$ là trung điểm của $BC \Rightarrow \overrightarrow {MB}  + \overrightarrow {MC}  = 2\overrightarrow {MI}$

$\Rightarrow \overrightarrow {AB}  = 2\overrightarrow {MI}$$\Rightarrow M$ là trung điểm $AC.$

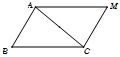
Ta có $\overrightarrow {MA}  + \overrightarrow {MC}  = \overrightarrow {MB}$ nên $MABC$ là hình bình hành

$\Rightarrow \overrightarrow {MA}  = \overrightarrow {CB}$

Do đó D sai.