Tam giác $ABC$ có $AB = AC = a$ và $\widehat {BAC} = 120^\circ$. Tính $\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right|.$

$\overrightarrow {MB}  = \overrightarrow {MC}$

$\overrightarrow {MA}  = \overrightarrow {MB}$

$\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0$

$\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {AC}  = \overrightarrow 0$

$\overrightarrow {AB}  + \overrightarrow {AC}  = \overrightarrow {BC} .$

$\overrightarrow {MP}  + \overrightarrow {NM}  = \overrightarrow {NP} .$

$\overrightarrow {CA}  + \overrightarrow {BA}  = \overrightarrow {CB} .$

$\overrightarrow {AA}  + \overrightarrow {BB}  = \overrightarrow {AB} .$

Nếu $M$ là trung điểm đoạn thẳng $AB$ thì $\overrightarrow {MA}  + \overrightarrow {MB}  = \overrightarrow 0 .$

Nếu $G$ là trọng tâm tam giác $ABC$ thì $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 .$

Nếu $ABCD$ là hình bình hành thì $\overrightarrow {CB}  + \overrightarrow {CD}  = \overrightarrow {CA} .$

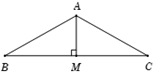
Nếu ba điểm phân biệt $A,\;B,\;C$ nằm tùy ý trên một đường thẳng thì $\left| {\overrightarrow {AB} } \right| + \left| {\overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right|.$

$G$ là tâm đường tròn ngoại tiếp tam giác $ABC$.

$G$ là tâm đường tròn nội tiếp tam giác $ABC$.

$G$ là trực tâm tam giác $ABC$.

$G$ là trọng tâm tam giác $ABC$.

$\overrightarrow {MI}  = \overrightarrow {MA}  + \overrightarrow {MB} .$

$\overrightarrow {MI}  = 2\left( {\overrightarrow {MA}  + \overrightarrow {MB} } \right).$

$\overrightarrow {MI}  = \dfrac{1}{2}\left( {\overrightarrow {MA}  + \overrightarrow {MB} } \right).$

$\overrightarrow {MI}  = 2\overrightarrow {MA}  + \overrightarrow {MB}.$

$IA = IB.$

$\overrightarrow {IA}  = \overrightarrow {IB} .$

$\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 .$

$\overrightarrow {AI}  = \overrightarrow {BI} .$