Trả lời bởi giáo viên
Đáp án đúng: d
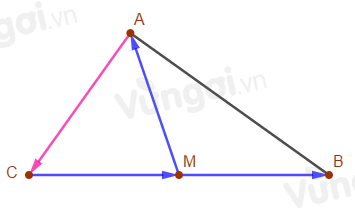
Ta có M là trung điểm của BC nên →CM=→MB
Suy ra
→MA+→MB+→AC=→MA+→CM+→AC=→CA+→AC=→0
Hướng dẫn giải:
M là trung điểm của BC nên →CM=→MB

