Tích của một véc tơ với một số

Vì $M$ là trung điểm $BC$ nên $\overrightarrow {AB}  + \overrightarrow {AC}  = 2\,\overrightarrow {AM} .$ $\left( 1 \right)$

Mặt khác $I$ là trung điểm $AM$ nên $2\,\overrightarrow {AI}  = \overrightarrow {AM} .$ $\left( 2 \right)$

Từ $\left( 1 \right),\,\,\left( 2 \right)$ suy ra $\overrightarrow {AB}  + \overrightarrow {AC}  = 4\overrightarrow {AI}$$\Leftrightarrow \overrightarrow {AI}  = \dfrac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$

Vì $G$ là trọng tâm của tam giác $ABC$$\Rightarrow \overrightarrow {AG}  = \dfrac{2}{3}\overrightarrow {AM} .$

Và $M$ là trung điểm của $BC$$\Rightarrow \overrightarrow {AB}  + \overrightarrow {AC}  = 2\overrightarrow {AM}$$\Leftrightarrow \overrightarrow {AM}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)$

Do đó $\overrightarrow {AG}  = \dfrac{2}{3}.\dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \dfrac{1}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right).$

Vì $M$ là trung điểm $BC$ nên $\overrightarrow {IB}  + \overrightarrow {IC}  = 2\overrightarrow {IM} .$

Mặt khác $I$ là trung điểm $AM$ nên $\overrightarrow {IA}  + \overrightarrow {IM}  = \overrightarrow 0 .$

Suy ra $\overrightarrow {IB}  + \overrightarrow {IC}  + 2\overrightarrow {IA}  = 2\overrightarrow {IM}  + 2\overrightarrow {IA}  = 2\left( {\overrightarrow {IM}  + \overrightarrow {IA} } \right) = \overrightarrow 0 .$

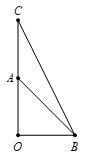
Gọi $C$ là điểm đối xứng của $O$ qua $A$$\Rightarrow OC = 2a.$

Tam giác $OBC$ vuông tại $O,$ có $BC = \sqrt {O{B^2} + O{C^2}}  = a\sqrt 5 .$

Ta có $2\overrightarrow {OA}  - \overrightarrow {OB}  = \overrightarrow {OC}  - \overrightarrow {OB}  = \overrightarrow {BC} ,$ suy ra $\left| {2\overrightarrow {OA}  - \overrightarrow {OB} } \right| = \left| {\overrightarrow {BC} } \right| = a\sqrt 5 .$

Ta có $\left\{ \begin{array}{l}\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {BC} \\\overrightarrow {BD}  = \overrightarrow {BC}  + \overrightarrow {CD} \end{array} \right.$ $\Rightarrow \overrightarrow {AC}  + \overrightarrow {BD}  = 2\overrightarrow {BC}  + \underbrace {\overrightarrow {AB}  + \overrightarrow {CD} }_{\overrightarrow 0 } = 2\overrightarrow {BC}$

Ta có $2\overrightarrow {MA}  + \overrightarrow {MB}  - 3\overrightarrow {MC}$$= 2\overrightarrow {MC}  + 2\overrightarrow {CA}  + \overrightarrow {MC}  + \overrightarrow {CB}  - 3\overrightarrow {MC}$ $= 2\overrightarrow {CA}  + \overrightarrow {CB}$

Dễ thấy $- 10\,\overrightarrow a  - 2\overrightarrow b  =  - \,2\,\left( {5\overrightarrow a  + \overrightarrow b } \right)$

$\Rightarrow$ hai vectơ $5\vec a + \vec b,\,\, - 10\vec a - 2\vec b$ cùng phương.

Gọi $I,\,\,G$ lần lượt là trung điểm $BC$ và trọng tâm tam giác $ABC.$

Vì $I$ là trung điểm $BC$ nên $\overrightarrow {MB}  + \overrightarrow {MC}  = 2\,\overrightarrow {MI} .$

Theo bài ra, ta có $\overrightarrow {MA}  = \overrightarrow {MB}  + \overrightarrow {MC}$ suy ra $\overrightarrow {MA}  = 2\overrightarrow {MI}$$\Rightarrow$$A,\,\,M,\,\,I$ thẳng hàng

Mặt khác $G$ là trọng tâm của tam giác $ABC$$\Rightarrow G \in AI.$

Do đó, ba điểm $A,\,\,M,\,\,G$ thẳng hàng.

Ta có:

$\overrightarrow {AM}  = x\overrightarrow {AB}  + y\overrightarrow {AC}$$\Leftrightarrow \overrightarrow {AM}  = x\left( {\overrightarrow {AM}  + \overrightarrow {MB} } \right) + y\left( {\overrightarrow {AM}  + \overrightarrow {MC} } \right)$

$\Leftrightarrow \left( {1 - x - y} \right)\overrightarrow {AM}  = x\overrightarrow {MB}  + y\overrightarrow {MC}$$\Leftrightarrow \left( {x + y - 1} \right)\overrightarrow {MA}  = x\overrightarrow {MB}  + y\overrightarrow {MC}$

Theo bài ra, ta có $\overrightarrow {MA}  = x\overrightarrow {MB}  + y\overrightarrow {MC}$ suy ra $x + y - 1 = 1 \Leftrightarrow x + y = 2.$

Ta có $\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AD}  + \overrightarrow {DN}$ và $\overrightarrow {MN}  = \overrightarrow {MB}  + \overrightarrow {BC}  + \overrightarrow {CN} .$

Suy ra $3\,\overrightarrow {MN}  = \overrightarrow {MA}  + \overrightarrow {AD}  + \overrightarrow {DN}  + 2\left( {\overrightarrow {MB}  + \overrightarrow {BC}  + \overrightarrow {CN} } \right)$

    $= \left( {\overrightarrow {MA}  + 2\overrightarrow {MB} } \right) + \overrightarrow {AD}  + 2\overrightarrow {BC}  + \left( {\overrightarrow {DN}  + 2\overrightarrow {CN} } \right).$

Theo bài ra, ta có $\overrightarrow {MA}  + 2\,\overrightarrow {MB}  = \overrightarrow 0$ và $\overrightarrow {DN}  + 2\,\overrightarrow {CN}  = \overrightarrow 0 .$

Vậy $3\,\overrightarrow {MN}  = \overrightarrow {AD}  + 2\,\overrightarrow {BC}  \Leftrightarrow \overrightarrow {MN}  = \dfrac{1}{3}\overrightarrow {AD}  + \dfrac{2}{3}\overrightarrow {BC} .$

Ta có $\overrightarrow {AN}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right) = \dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AC}$

$\overrightarrow {CM}  = \overrightarrow {CA}  + \overrightarrow {AM}  \Rightarrow \dfrac{1}{2}\overrightarrow {CM}  = \dfrac{1}{2}\overrightarrow {CA}  + \dfrac{1}{2}\overrightarrow {AM}$

Suy ra $\overrightarrow {AN}  + \dfrac{1}{2}\overrightarrow {CM}  = \dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AC}  + \dfrac{1}{2}\overrightarrow {CA}  + \dfrac{1}{2}\overrightarrow {AM}  = \dfrac{1}{2}\overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AC}  - \dfrac{1}{2}\overrightarrow {AC}  + \dfrac{1}{2} \cdot \dfrac{1}{2}\overrightarrow {AB}  = \dfrac{3}{4}\overrightarrow {AB}$

Do đó $\overrightarrow {AB}  = \dfrac{4}{3}\overrightarrow {AN}  + \dfrac{2}{3}\overrightarrow {CM}$.

Gọi $E,\,\,F$ lần lượt là trung điểm của $AB,\,\,CD.$

Khi đó $\left\{ \begin{array}{l}\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {ME} \\\overrightarrow {MC}  + \overrightarrow {MD}  = 2\overrightarrow {MF} \end{array} \right.,\,\,\forall M.$

Do đó $\left| {\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MC}  + \overrightarrow {MD} } \right|$ $\Leftrightarrow 2\left| {\overrightarrow {ME} } \right| = 2\left| {\overrightarrow {MF} } \right| \Leftrightarrow \left| {\overrightarrow {ME} } \right| = \left| {\overrightarrow {MF} } \right|$ $\left(  *  \right)$

Vì $E,\,\,F$ là hai điểm cố định nên từ đẳng thức $\left(  *  \right)$suy ra tập hợp các điểm $M$ là trung trực của đoạn thẳng $EF$ hay chính là trung trực của đoạn thẳng $AD.$

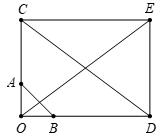
Dựa vào các đáp án, ta có nhận xét sau:

A đúng, gọi $C$ nằm trên tia đối của tia $AO$ sao cho $OC = 3\,OA$$\Rightarrow 3\,\overrightarrow {OA}  = \overrightarrow {OC} .$

Và $D$ nằm trên tia đối của tia $BO$ sao cho $OD = 4\,OB$$\Rightarrow 4\,\overrightarrow {OB}  = \overrightarrow {OD} .$

Dựng hình chữ nhật $OCED$ suy ra $\overrightarrow {OC}  + \overrightarrow {OD}  = \overrightarrow {OE}$ (quy tắc hình bình hành).

Ta có $\left| {3\overrightarrow {OA}  + 4\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC}  + \overrightarrow {OD} } \right| = \left| {\overrightarrow {OE} } \right| = OE = CD = \sqrt {O{C^2} + O{D^2}}  = 5a.$

B đúng, vì $\left| {2\,\overrightarrow {OA} } \right| + \left| {3\,\overrightarrow {OB} } \right| = 2\left| {\overrightarrow {OA} } \right| + 3\left| {\overrightarrow {OB} } \right| = 2a + 3a = 5a.$

C sai, xử lý tương tự như ý đáp án A.

D đúng, vì $\left| {11\,\overrightarrow {OA} } \right| - \left| {6\,\overrightarrow {OB} } \right| = 11\left| {\overrightarrow {OA} } \right| - 6\left| {\overrightarrow {OB} } \right| = 11a - 6a = 5a.$

Chọn điểm $E$ thuộc đoạn $AB$ sao cho $EB = 2EA$$\Rightarrow 2\overrightarrow {EA}  + \overrightarrow {EB}  = \overrightarrow 0 .$

Chọn điểm $F$ thuộc đoạn $AB$ sao cho $FA = 2FB$$\Rightarrow 2\overrightarrow {FB}  + \overrightarrow {FA}  = \overrightarrow 0 .$

Ta có

    $\left| {2\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  + 2\overrightarrow {MB} } \right| \Leftrightarrow \left| {2\overrightarrow {ME}  + 2\overrightarrow {EA}  + \overrightarrow {ME}  + \overrightarrow {EB} } \right| = \left| {2\overrightarrow {MF}  + 2\overrightarrow {FB}  + \overrightarrow {MF}  + \overrightarrow {FA} } \right|$

$\Leftrightarrow \left| {3\,\overrightarrow {ME}  + \underbrace {2\,\overrightarrow {EA}  + \overrightarrow {EB} }_{\overrightarrow 0 }} \right| = \left| {3\,\overrightarrow {MF}  + \underbrace {2\,\overrightarrow {FA}  + \overrightarrow {FB} }_{\overrightarrow 0 }} \right| \Leftrightarrow \left| {3\,\overrightarrow {ME} } \right| = \left| {3\,\overrightarrow {MF} } \right| \Leftrightarrow ME = MF.$ $\,\left(  *  \right)$

Vì $E,\,\,F$ là hai điểm cố định nên từ đẳng thức $\left(  *  \right)$ suy ra tập hợp các điểm $M$ là trung trực của đoạn thẳng $EF.$

Gọi $I$ là trung điểm của $AB$ suy ra $I$ cũng là trung điểm của $EF.$

Vậy tập hợp các điểm $M$ thỏa mãn $\left| {2\overrightarrow {MA}  + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA}  + 2\overrightarrow {MB} } \right|$ là đường trung trực của đoạn thẳng $AB.$

Gọi $G$ là trọng tâm của tam giác $ABC$ nên G cố định duy nhất và $\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0$.Ta có $\left| {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} } \right| = 3\,\, \Leftrightarrow \,\,\left| {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  - 3\overrightarrow {GM} } \right| = 3\,\, \Leftrightarrow \,3\,\left| {\overrightarrow {GM} } \right| = 3\,\, \Leftrightarrow \,\,GM = 1$.Vậy tập hợp các điểm $M$ là đường tròn tâm $G$ bán kính bằng $1.$

Bước 1:

Ta có $AB\parallel CD$ nên theo hệ quả định lý Ta-lét ta được:

$\dfrac{{BM}}{{MD}} = \dfrac{{AB}}{{CD}} = \dfrac{1}{2}$$\Rightarrow MD = 2BM$

Mà $BD = BM + MD$

$\Rightarrow BD = BM + 2BM = 3BM$$\Rightarrow BM = \dfrac{1}{3}BD$

$\Rightarrow \overrightarrow {BM}  = \dfrac{1}{3}\overrightarrow {BD}$

Bước 2:

$\begin{array}{l} \Rightarrow \overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM}  = \overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {BD} \\ = \overrightarrow {AB}  + \dfrac{1}{3}\left( {\overrightarrow {BA}  + \overrightarrow {AD} } \right) = \dfrac{2}{3}\overrightarrow {AB}  + \dfrac{1}{3}\overrightarrow {AD} \end{array}$

Ta có ba điểm phân biệt $A,{\rm{ }}B,{\rm{ }}C$ thẳng hàng khi và chỉ khi các véc tơ $\overrightarrow {AB}, \overrightarrow {AC},\overrightarrow {BC}$ cùng phương, hay $\exists {\rm{ }}k \in \mathbb{R},k \ne 0$ sao cho $\overrightarrow {AB} {\rm{  =  }}k\overrightarrow {AC}$ hoặc $\overrightarrow {AB} {\rm{  =  }}k\overrightarrow {BC}$ hoặc $\overrightarrow {AC} {\rm{  =  }}k\overrightarrow {BC}$

Chú ý rằng hệ số $k$ phải khác $0$ nên chỉ có đáp án D sai.

Ta có $\overrightarrow a  =  - 2\overrightarrow b {\rm{ }}$ $\Rightarrow {\rm{ }}\overrightarrow c  = \overrightarrow a  + \overrightarrow b$ $=  - 2\overrightarrow b  + \overrightarrow b  =  - \overrightarrow b$

Vậy hai vectơ $\overrightarrow b ,\overrightarrow c$ đối nhau.

Do đó chúng cùng phương, ngược hướng nên các đáp án B, C, D đúng.

Đáp án A sai vì hai véc tơ đó không bằng nhau.

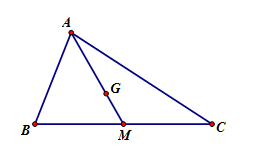
Ta có $GA = \dfrac{2}{3}AM$

Mặt khác $\overrightarrow {GA}$ và $\overrightarrow {AM}$ ngược hướng $\overrightarrow {GA}  =  - \dfrac{2}{3}\overrightarrow {AM}$.

Ta có $AM = 3MG$

Mặt khác $\overrightarrow {AM}$ và $\overrightarrow {MG}$ ngược hướng

$\Rightarrow \overrightarrow {AM}  =  - 3\overrightarrow {MG}$.