Câu hỏi:
2 năm trước
Cho tam giác \(OAB\) vuông cân tại \(O,\) cạnh \(OA = a.\) Tính \(\left| {2\overrightarrow {OA} - \overrightarrow {OB} } \right|.\)
Trả lời bởi giáo viên
Đáp án đúng: c
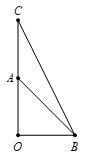
Gọi \(C\) là điểm đối xứng của \(O\) qua \(A\)\( \Rightarrow OC = 2a.\)
Tam giác \(OBC\) vuông tại \(O,\) có \(BC = \sqrt {O{B^2} + O{C^2}} = a\sqrt 5 .\)
Ta có \(2\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {BC} ,\) suy ra \(\left| {2\overrightarrow {OA} - \overrightarrow {OB} } \right| = \left| {\overrightarrow {BC} } \right| = a\sqrt 5 .\)
Hướng dẫn giải:
Tính hiệu các véc tơ rồi suy ra độ dài dựa vào kiến thức hình học đã biết.
