Trên đường thẳng $MN$ lấy điểm $P$ sao cho \(\overrightarrow {MN} = - 3\overrightarrow {MP} \). Điểm $P$ được xác định đúng trong hình vẽ nào sau đây:
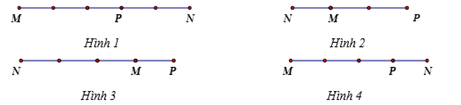
Ta có \(\overrightarrow {MN} = - 3\overrightarrow {MP} \) nên \(MN = 3MP\) và\(\overrightarrow {MN} \) và \(\overrightarrow {MP} \) ngược hướng.
Hãy chọn kết quả đúng khi phân tích vectơ $\overrightarrow {AM} $ theo hai véctơ $\overrightarrow {AB} $và$\overrightarrow {AC} $ của tam giác \(ABC\) với trung tuyến $AM$.
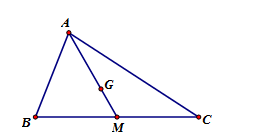
Do $M$ là trung điểm của $BC$nên ta có $\overrightarrow {AM} = \dfrac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} )$.
Nếu \(G\) là trọng tam giác $ABC$ thì đẳng thức nào sau đây đúng.
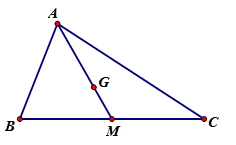
Gọi $M$ là trung điểm của $BC$ nên ta có
$\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} $
Mà \(\overrightarrow {AM} = \dfrac{3}{2}\overrightarrow {AG} \)$ \Rightarrow \overrightarrow {AB} + \overrightarrow {AC} = 2.\dfrac{3}{2}\overrightarrow {AG} = 3\overrightarrow {AG} $$ \Rightarrow \overrightarrow {AG} = \dfrac{{\overrightarrow {AB} + \overrightarrow {AC} }}{3}$.
Đẳng thức nào sau đây mô tả đúng hình vẽ bên:
Ta có $AB = 3AI;\,\,\,\overrightarrow {AI} $ và $\overrightarrow {AB} $ ngược hướng nên $\overrightarrow {AB} = - 3\overrightarrow {AI} \Leftrightarrow $$3\overrightarrow {AI} + \overrightarrow {AB} = \overrightarrow 0 $
Vậy $3\overrightarrow {AI} + \overrightarrow {AB} = \overrightarrow 0 $.
Cho hình vuông \(ABCD\) cạnh $\;a\sqrt 2 $. Tính$S = \left| {2\overrightarrow {AD} + \overrightarrow {DB} } \right|$?
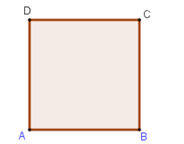
Ta có
$S = \left| {2\overrightarrow {AD} + \overrightarrow {DB} } \right| = \left| {\overrightarrow {AD} + \overrightarrow {AD} + \overrightarrow {DB} } \right|$$ = \left| {\overrightarrow {AD} + \overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right| = a\sqrt 2 .\sqrt 2 = 2a$.
Phát biểu nào là sai?
$\overrightarrow {AB} = \overrightarrow {CD} $ thì \(\left[ \begin{array}{l}AB//CD\\AB \equiv CD\end{array} \right.\).
Nên đáp án B SAI.
Cho hai tam giác $ABC$ và $A'B'C'$ lần lượt có trọng tâm là $G$ và $G'$. Đẳng thức nào sau đây là sai?
Do $G$ và $G'$ lần lượt là trọng tâm của tam giác $ABC$và $A'B'C'$ nên
$\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} = \overrightarrow 0 $ và $\overrightarrow {A'G'} + \overrightarrow {B'G'} + \overrightarrow {C'G'} = \overrightarrow 0 $
Đáp án A: $\overrightarrow {AA'} + \overrightarrow {BB'} + \overrightarrow {CC'} = \left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) + \left( {\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} } \right) = \overrightarrow 0 + 3\overrightarrow {GG'} $
Đáp án B: $\overrightarrow {AB'} + \overrightarrow {BC'} + \overrightarrow {CA'} = \left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) + \left( {\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} } \right) = \overrightarrow 0 + 3\overrightarrow {GG'} $
Đáp án C: $\overrightarrow {AC'} + \overrightarrow {BA'} + \overrightarrow {CB'} = \left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) + \left( {\overrightarrow {GA'} + \overrightarrow {GB'} + \overrightarrow {GC'} } \right) = \overrightarrow 0 + 3\overrightarrow {GG'} $
Đáp án D: $\overrightarrow {A'A} + \overrightarrow {B'B} + \overrightarrow {C'C} = \left( {\overrightarrow {A'G'} + \overrightarrow {B'G'} + \overrightarrow {C'G'} } \right) + \left( {\overrightarrow {G'A} + \overrightarrow {G'B} + \overrightarrow {G'C} } \right) = \overrightarrow 0 + 3\overrightarrow {G'G} $ (SAI)
Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ không cùng phương. Hai vectơ nào sau đây cùng phương?
Ta có\(\dfrac{1}{2}\overrightarrow a - \overrightarrow b = - \left( { - \dfrac{1}{2}\overrightarrow a + \overrightarrow b } \right)\) nên chọn đáp án C.
Biết rằng hai vec tơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương nhưng hai vec tơ \(2\overrightarrow a - 3\overrightarrow b \) và \(\overrightarrow a + \left( {x - 1} \right)\overrightarrow b \) cùng phương. Khi đó giá trị của \(x\) là:
Ta có \(2\overrightarrow a - 3\overrightarrow b \) và \(\overrightarrow a + \left( {x - 1} \right)\overrightarrow b \) cùng phương nên có tỉ lệ:\(\dfrac{1}{2} = \dfrac{{x - 1}}{{ - 3}} \Rightarrow x = - \dfrac{1}{2}\).
Cho tam giác $ABC$, điểm \(M\) thoả mãn: $5\overrightarrow {MA} = 2\overrightarrow {MB} $. Với mỗi điểm \(I\) bất kì, nếu $\overrightarrow {IA} = m\overrightarrow {IM} + n\overrightarrow {IB} $ thì cặp số $\left( {m;n} \right)$ bằng:
Ta có
$5\overrightarrow {MA} = 2\overrightarrow {MB} \Leftrightarrow 5\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) = 2\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right) \Leftrightarrow 5\overrightarrow {IA} = 3\overrightarrow {IM} + 2\overrightarrow {IB} \Leftrightarrow \overrightarrow {IA} = \dfrac{3}{5}\overrightarrow {IM} + \dfrac{2}{5}\overrightarrow {IB} $
Cho tam giác $ABC$. Gọi \(M\) là điểm trên cạnh $BC$ sao cho $MB = 3MC$. Khi đó, biễu diễn $\overrightarrow {AM} $ theo $\overrightarrow {AB} $ và $\overrightarrow {AC} $ là:
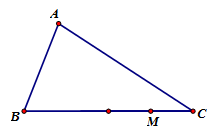
Ta có:
$\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} $ $= \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right) $ $= \dfrac{1}{4}\overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {AC} $
Cho tam giác $ABC$ có $M$ thuộc cạnh $BC$ sao cho $CM{\rm{ }} = {\rm{ }}2MB$ và $I$ là trung điểm của$AB$. Đẳng thức nào sau đây đúng?
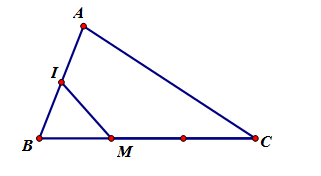
Ta có
$\overrightarrow {IM} = \overrightarrow {IB} + \overrightarrow {BM} = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {BC} = \dfrac{1}{2}\overrightarrow {AB} + \dfrac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) $ $= \dfrac{1}{6}\overrightarrow {AB} + \dfrac{1}{3}\overrightarrow {AC} $.
Cho hai điểm cố định \(A,B\); gọi \(I\) là trung điểm \(AB\). Tập hợp các điểm \(M\) thoả: \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\) là:
Ta có \(\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\)\( \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| {\overrightarrow {BA} } \right| \Leftrightarrow 2MI = BA \Leftrightarrow MI = \dfrac{{BA}}{2}\)
Vậy tập hợp các điểm \(M\) là đường tròn đường kính \(AB\).
Tam giác \(ABC\) vuông tại $A,{\rm{ }}AB = AC = 2$. Độ dài vectơ $4\overrightarrow {AB} - \overrightarrow {AC} $bằng:
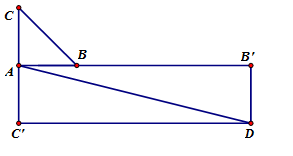
Vẽ $\overrightarrow {AB'} = 4\overrightarrow {AB} ;\,\,\,\,\,\,\overrightarrow {AC'} = - \overrightarrow {AC} $. Vẽ hình bình hành $AC'DB'$
Ta có: $\left| {4\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB'} + \overrightarrow {AC'} } \right| = \left| {\overrightarrow {AD} } \right| = AD$
Do đó $AD = \sqrt {A{{B'}^2} + A{{C'}^2}} = \sqrt {{8^2} + {2^2}} = 2\sqrt {17} $.
Cho tam giác đều \(ABC\) cạnh \(a.\) Biết rằng tập hợp các điểm \(M\) thỏa mãn đẳng thức \(\left| {2\overrightarrow {MA} + 3\overrightarrow {MB} + 4\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB} - \overrightarrow {MA} } \right|\) là đường tròn cố định có bán kính \(R.\) Tính bán kính \(R\) theo \(a.\)
Gọi \(G\) là trọng tâm của tam giác \(ABC.\)
Ta có \(2\overrightarrow {MA} + 3\overrightarrow {MB} + 4\overrightarrow {MC} \)\( = 2\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) + 3\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right) + 4\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)\)
Chọn điểm \(I\) sao cho \(2\overrightarrow {IA} + 3\overrightarrow {IB} + 4\overrightarrow {IC} = \overrightarrow 0 \)\( \Leftrightarrow 3\left( {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} } \right) + \overrightarrow {IC} - \overrightarrow {IA} = \overrightarrow 0 .\)
Mà \(G\) là trọng tâm của tam giác \(ABC\)\( \Rightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = 3\,\overrightarrow {IG} .\)
Khi đó \(9\,\overrightarrow {IG} + \overrightarrow {IC} - \overrightarrow {IA} = \overrightarrow 0 \) \( \Leftrightarrow 9\overrightarrow {IG} + \overrightarrow {AI} + \overrightarrow {IC} = \overrightarrow 0 \) \( \Leftrightarrow 9\overrightarrow {IG} = \overrightarrow {CA} \) \(\left( * \right)\)
Do đó \(\left| {2\overrightarrow {MA} + 3\overrightarrow {MB} + 4\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB} - \overrightarrow {MA} } \right|\)\( \Leftrightarrow \left| {9\overrightarrow {MI} + 2\overrightarrow {IA} + 3\overrightarrow {IB} + 4\overrightarrow {IC} } \right| = \left| {\overrightarrow {AB} } \right|\) \( \Leftrightarrow 9MI = AB\)
Vì \(I\) là điểm cố định thỏa mãn \(\left( * \right)\) nên tập hợp các điểm \(M\) cần tìm là đường tròn tâm \(I,\) bán kính \(R = \dfrac{{AB}}{9} = \dfrac{a}{9}.\)
Cho tam giác $ABC$, tập hợp các điểm $M$ sao cho $\left| {\,\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \,} \right| = 6$ là:
Gọi $G$ là trọng tâm của tam giác $ABC$ , ta có $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} $.
Thay vào ta được : $\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 6 \Leftrightarrow \left| {3\overrightarrow {MG} } \right| = 6 \Leftrightarrow MG = 2$, hay tập hợp các điểm $M$là đường tròn có tâm là trọng tâm của tam giác $ABC$ và bán kính bằng $2$ .
Cho hình thang \(ABCD\) có \(AB\parallel CD\) và CD=2AB, E là trung điểm của BC. F là điểm thỏa mãn \(\overrightarrow {BF} = \dfrac{2}{3}\overrightarrow {AB} \). Tồn tại x sao cho \(\overrightarrow {MC} = x\overrightarrow {CD} \), tìm x để M, E, F thẳng hàng.
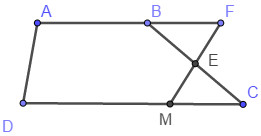
Ta có: M, E, F thẳng hàng nên theo hệ quả của định lí Ta-let ta có: \(\dfrac{{FE}}{{EM}} = \dfrac{{BE}}{{CE}} = \dfrac{1}{2}\) hay E là trung điểm của MF. Khi đó
\(\overrightarrow {MC} = \overrightarrow {BF} = \dfrac{2}{3}\overrightarrow {AB} = \dfrac{2}{3}.\dfrac{1}{2}\overrightarrow {DC} = \dfrac{1}{3}\overrightarrow {DC} = - \dfrac{1}{3}\overrightarrow {CD} \).
Vậy \(x = - \dfrac{1}{3}\)
