Cho hai tập hợp: \(A = \left\{ {1;2;3;4;5;6;7} \right\},B = \left\{ {0;2;4;6;8;10} \right\}\). Tính số phần tử của \(A \cap B\).
Ta có: \(A = \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7} \right\}\) và \(B = \left\{ {0;\,\,2;\,\,4;\,\,6;\,\,8;\,\,10} \right\}\)
Các phần tử chung của $A$ và $B$ là $2;4;6$.
\( \Rightarrow A \cap B = \left\{ {2;4;6} \right\}.\)
Số phần tử của \(A \cap B\) là 3.
Cho các tập hợp \(M = {\rm{\{ }}x \in \mathbb{N}\left| x \right.\) là bội của \(2\} \), $N = {\rm{\{ }}x \in \mathbb{N}\left| x \right.$ là bội của \(6\} \), \(P = {\rm{\{ }}x \in \mathbb{N}\left| x \right.\) là ước của \(2\} \), \(Q = {\rm{\{ }}x \in \mathbb{N}\left| x \right.\) là ước của \(6\} .\) Mệnh đề nào sau đây sai?
Ta có các tập hợp \(\left\{ \begin{array}{l}M = \left\{ {x\left| {x = 2k,\;k \in \mathbb{N}} \right.} \right\} = \left\{ {0;2;4;6;8;10;...} \right\}\\N = \left\{ {x\left| {x = 6k,\;k \in \mathbb{N}} \right.} \right\} = \left\{ {0;6;12;18;24;...} \right\}\\P = \left\{ {1;2} \right\}\\Q = \left\{ {1;2;3;6} \right\}\end{array} \right.\).
Do đó \(P \subset Q \Rightarrow P \cap Q = P,\)\(N \subset M \Rightarrow M \cap N = N\) .
Cho hai tập \(A = \left\{ {x \in \mathbb{R}\left| {\left( {2x - {x^2}} \right)\left( {2{x^2} - 3x - 2} \right) = 0} \right.} \right\}\) và \(B = \left\{ {n \in {\mathbb{N}^ * }\left| {3 < {n^2} < 30} \right.} \right\}\). Tìm \(A \cap B.\)
Ta có
\(\left( {2x - {x^2}} \right)\left( {2{x^2} - 3x - 2} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}2x - {x^2} = 0\\2{x^2} - 3x - 2 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x\left( {2 - x} \right) = 0\\\left( {x - 2} \right)\left( {2x + 1} \right) = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = - \dfrac{1}{2}\end{array} \right. \Rightarrow A = \left\{ { - \dfrac{1}{2};0;2} \right\}\)
Và \(\left\{ \begin{array}{l}n \in {\mathbb{N}^ * }\\3 < {n^2} < 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n \in {\mathbb{N}^ * }\\\sqrt 3 < n < \sqrt {30} \end{array} \right.\) \( \Rightarrow B = \left\{ {2;3;4;5} \right\}\)
Suy ra \(A \cap B = \left\{ 2 \right\}.\)
Gọi \({B_n}\) là tập hợp các bội số của \(n\) trong \(\mathbb{N}\). Xác định tập hợp \({B_2} \cap {B_4}\)?
Ta có các tập hợp \(\left\{ \begin{array}{l}{B_2} = \left\{ {x\left| {x = 2k,\;k \in {\mathbb{N}^ * }} \right.} \right\} = \left\{ {2;4;6;8;10;...} \right\}\\{B_4} = \left\{ {x\left| {x = 4k,\;k \in {\mathbb{N}^ * }} \right.} \right\} = \left\{ {4;8;12;16;...} \right\}\end{array} \right.\).
Do đó \({B_2} \cap {B_4} = {B_4}\).
Cho hai tập hợp \(A = \left\{ {a;\;b;\;c;\;d;\;m} \right\},\)\(B = \left\{ {c;\;d;\;m;\;k;\;l} \right\}\). Tìm \(A \cap B\).
Tập hợp \(A\) và tập hợp \(B\) có chung các phần tử \(c,\;d,\;m\).
Do đó \(A \cap B = \left\{ {c;\;d;\;m} \right\}\).
Cho hai tập hợp $X = \left\{ {1;a;b} \right\},$$Y = \left\{ {3;5} \right\}$. Tập hợp $X \cup Y$ bằng tập hợp nào sau đây ?
$X = \left\{ {1;a;b} \right\},$$Y = \left\{ {3;5} \right\}$\( \Rightarrow X \cup Y = \left\{ {1;a;b;3;5} \right\}\).
Cho tập $A \ne \emptyset $ . Trong các mệnh đề sau, tìm mệnh đề sai ?
Ta có: \(\emptyset \subset A;A \subset A;\emptyset \subset \emptyset \) nên $A \cap A = A;\emptyset \cap A = \emptyset ;\emptyset \cap \emptyset = \emptyset $.
Do đó các đáp án A, C, D đều đúng.
Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},\;B = \left\{ {2;3;4;5;6} \right\}\). Xác định tập hợp \(A\backslash B.\)
Tập hợp \(A\backslash B\) gồm những phần tử thuộc \(A\) nhưng không thuộc \(B\)
\( \Rightarrow A\backslash B = \left\{ 0;1 \right\}\).
Cho hai tập hợp \(A = \left\{ {0;1;2;3;4} \right\},B = \left\{ {2;3;4;5;6} \right\}\). Xác định tập hợp \(B\backslash A.\)
Tập hợp \(B\backslash A\) gồm những phần tử thuộc \(B\) nhưng không thuộc \(A\)
\( \Rightarrow B\backslash A = \left\{ {5;6} \right\}\).
Cho \(A\) là tập hợp tất cả các nghiệm của phương trình ${x^2} - 4x + 3\; = 0$; \(B\) là tập hợp các số có giá trị tuyệt đối nhỏ hơn 4. Khẳng định nào sau đây đúng?
Ta có ${x^2} - 4x + 3\; = 0 \Leftrightarrow \left\{ \begin{array}{l}x = 1\\x = 3\end{array} \right.$$ \Rightarrow A = \left\{ {1;3} \right\}$
\(B = \left\{ { - 3; - 2; - 1;0;1;2;3} \right\}\). Do đó $A\backslash B = \emptyset $.
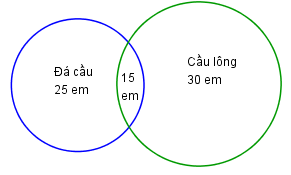
Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em biết chơi cầu lông, 15 em biết chơi cả hai . Hỏi lớp 10A1 có bao nhiêu em?
Dựa vào biểu đồ ven ta suy ra số học sinh chỉ biết đá cầu là \(25 - 15 = 10\) (học sinh).
Số học sinh chỉ biết đánh cầu lông là \(30 - 15 = 15\) (học sinh).
Do đó ta có sĩ số học sinh của lớp 10A1 là \(10 + 15 + 15 = 40\) (học sinh).
Cho các tập hợp \(E = \{ {\rm{ }}x \in \mathbb{N}|1 \le x < 7\} ,\,\)\(A = \{ {\rm{ }}x \in \mathbb{N}|\left( {{x^2} - 9} \right)\left( {{x^2}-5x-6} \right) = 0\} \) và \(B = {\rm{\{ }}x \in \mathbb{N}|x\) là số nguyên tố nhỏ hơn 6}. Khẳng định nào sau đây là đúng nhất?
Ta có: \(\left( {{x^2} - 9} \right)\left( {{x^2} - 5x - 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} - 9 = 0\\{x^2} - 5x - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 3\\x = - 1\\x = 6\end{array} \right..\)
\( \Rightarrow A = \left\{ {\left. {x \in \mathbb{N}} \right|\left( {{x^2} - 9} \right)\left( {{x^2} - 5x - 6} \right) = 0} \right\} \)\(= \left\{ {3;\,\,6} \right\}\)
Các số nguyên tố nhỏ hơn \(6\) là: \(2;\,\,3;\,\,5.\)
=> \(B = \left\{ {2;\,\,3;\,\,5} \right\}.\)
\( \Rightarrow E = \left\{ {\left. {x \in \mathbb{N}} \right|\,1 \le x < 7} \right\} \)\(= \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6} \right\};\)
\(\begin{array}{l} \Rightarrow {C_E}A = E\backslash A = \left\{ {1;\,2;\,4;\,5} \right\};\\{\rm{ }}{C_E}B = E\backslash B = \left\{ {1;\,4;\,6} \right\}\\ \Rightarrow A \cup B = \left\{ {2;\,3;\,5;\,6} \right\} \\\Rightarrow {C_E}(A \cup B) = E\backslash \left( {A \cup B} \right) = \left\{ {1;\,4} \right\}.\end{array}\)
Cho các tập hợp: \(A = \left\{ {\left. {x \in \mathbb{R}} \right|\,\left( {{x^2} + 7x + 6} \right)\left( {{x^2} - 4} \right) = 0} \right\};\) \(B = \left\{ {x \in \mathbb{N}|\,2x \le 8} \right\}\); \(C = {\rm{\{ }}2x + 1|\,x \in \mathbb{Z};\,\,\, - 2 \le x \le 4{\rm{.}}\) Tìm \(\left( {A \cup C} \right)\backslash B.\)
\( \bullet \) Ta có: \(\left( {{x^2} + 7x + 6} \right)\left( {{x^2} - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} + 7x + 6 = 0\\{x^2} - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 6\\x = - 2\\x = 2\end{array} \right..\)
Vậy \(A = \left\{ { - 6; - 2; - 1;2} \right\}.\)
\( \bullet \) Ta có: \(\left\{ \begin{array}{l}x \in \mathbb{N}\\2x \le 8\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x \in \mathbb{N}\\x \le 4\end{array} \right. \)\(\Leftrightarrow x \in \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\)
Vậy \(B = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}.\)
\( \bullet \) Ta có: \(\left\{ \begin{array}{l}x \in \mathbb{Z}\\ - 2 \le x \le 4\end{array} \right.\)\( \Leftrightarrow x \in \left\{ { - 2; - 1;\,\,0;\,\,1;\,\,2;\,\,3 ;\,\,4} \right\} \)\(\Rightarrow \left( {2x + 1} \right) \in \left\{ { - 3; - 1;\,1;\,3;\,\,5;\,\,7;\,\,9} \right\}.\)
\( \Rightarrow C = \left\{ { - 3; - 1;\,1;\,3;\,5;\,7;\,9} \right\}\)
Ta có: \(A \cup C = \left\{ { - 6; - 3; - 2; - 1;1;2;3;5;7;9} \right\}\)
\( \Rightarrow \left( {A \cup C} \right)\backslash B = \left\{ { - 6; - 3; - 2; - 1;\,5;\,7;\,9} \right\}.\)
Cho hai tập hợp \(A = \left\{ { - 1;0;2;5} \right\}\) và \(B = \left\{ {1;2;3;5} \right\}\). Xác định tập hợp \(A\backslash B\).
\(A = \left\{ { - 1;0;2;5} \right\}\) và \(B = \left\{ {1;2;3;5} \right\}\)
Phần tử thuộc $A$ mà không thuộc $B$ là: $- 1;0$
\( \Rightarrow A\backslash B = \left\{ { - 1;0} \right\}\).
Cho \(A = \left\{ {2;5} \right\};\,\,B = \left\{ {2;3;5} \right\}\). Tập hợp \(A \cup B\) là
\(A = \left\{ {2;5} \right\};\,\,B = \left\{ {2;3;5} \right\}\)
$A \subset B$ nên
\(A \cup B =B= \left\{ {2;3;5} \right\}\).
Cho hai tập hợp \(X = \left\{ {1;2;4;7;9} \right\};\,\,Y = \left\{ { - 1;0;7;10} \right\}\), tập hợp \(X \cup Y\) có bao nhiêu phần tử?
\(X \cup Y = \left\{ { - 1;0;1;2;4;7;9;10} \right\}\).
Vậy \(X \cup Y \) có 8 phần tử.
Cho \(A\) là tập hợp các học sinh nam trong lớp em và \(B\) là tập hợp các học sinh cao từ 1m70 trở lên của lớp em. Tập hợp \(A\backslash B\) là
\(A\backslash B\) là tập hợp các phần tử thuộc \(A\) mà không thuộc \(B\) nên \(A\backslash B\) là tập hợp các học sinh nam cao dưới 1m70.
Cho tập hợp A = {0;1;2;3;4} và B = {0;2;4;6;8}. Hỏi tập hợp \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) có bao nhiêu phần tử?
Ta có:
A \ B = {1;3} , B \ A = {6;8}
\( \Rightarrow \left( {A\backslash B} \right) \cup \left( {B\backslash A} \right) = \left\{ {1;3;6;8} \right\}\).
Vậy \(\left( {A\backslash B} \right) \cup \left( {B\backslash A} \right)\) có 4 phần tử.
Cho hai tập hợp: $A = \{ x|x$ là ước số nguyên dương của $12\} $
$B = \{ x|\;x$ là ước số nguyên dương của $18\} $
Tập hợp $A \cap B$ là:
\(A = \left\{ {1;2;3;4;6;12} \right\}\) và \(B = \left\{ {1;2;3;6;9;18} \right\}\)
Khi đó $A \cap B = \left\{ {1;2;3;6} \right\}$.
Cho hai tập \(A = \{ x \in R\left| {x + 3 < 4 + 2x\} } \right.\) và \(B = \{ x \in R\left| {5x - 3 < 4x - 1\} } \right.\)
Tất cả các số tự nhiên thuộc cả hai tập $A$ và $B$ là:
\(A = \{ x \in R\left| {x + 3 < 4 + 2x\} } \right. = \left\{ {x \in R| - x < 1} \right\} = \left\{ {x \in R|x > - 1} \right\}\)
\(B = \{ x \in R\left| {5x - 3 < 4x - 1\} } \right. = \left\{ {x \in R|x < 2} \right\}\)
Do đó \(A \cap B = \left\{ {x \in R| - 1 < x < 2} \right\}\).
Mà \(x\) là số tự nhiên nên \(x = 0\) hoặc \(x = 1\).