Tập nghiệm của bất phương trình: $-{x^2} + 6x + 7\; \ge 0\;$là:
Ta có $-{x^2} + 6x + 7\; = 0 \Leftrightarrow \left[ \begin{array}{l}x = 7\\x = - 1\end{array} \right.$.
Bảng xét dấu
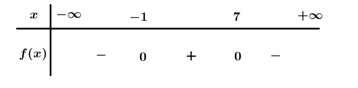
Dựa vào bảng xét dấu $-{x^2} + 6x + 7\; \ge 0 \Leftrightarrow - 1 \le x \le 7.$
Hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} - 9 < 0\,\,\left( 1 \right)\\(x - 1)(3{x^2} + 7x + 5) \ge 0\,\,\left( 2 \right)\end{array} \right.\) có nghiệm là:
Ta có: \({x^2} - 9 < 0 \Leftrightarrow \left( {x - 3} \right)\left( {x + 3} \right) < 0\) \( \Leftrightarrow - 3 < x < 3\)
Tập nghiệm của \(\left( 1 \right)\) là \({S_1} = \left( { - 3;3} \right).\)
Xét tam thức \(f\left( x \right) = 3{x^2} + 7x + 5\) có \(\Delta = - 11 < 0\) nên \(f\left( x \right) > 0,\forall x \in \mathbb{R}\).
Khi đó \((x - 1)(3{x^2} + 7x + 4) \ge 0\) \( \Leftrightarrow x - 1 \ge 1 \Leftrightarrow x \ge 1\).
Tập nghiệm của \(\left( 2 \right)\) là \({S_2} = \left[ {1; + \infty } \right)\).
Vậy tập nghiệm của hệ là \(S = {S_1} \cap {S_2} = \left[ {1;3} \right).\)
Bất phương trình $\dfrac{{2{x^2} - x - 1}}{{\left| {x + 1} \right| - 2x}} \le - 2{x^2} + x + 1$ có bao nhiêu nghiệm nguyên?
- Nếu \(x \ge - 1\) thì $\dfrac{{2{x^2} - x - 1}}{{\left| {x + 1} \right| - 2x}} \le - 2{x^2} + x + 1$$ \Leftrightarrow \dfrac{{2{x^2} - x - 1}}{{1 - x}} \le - 2{x^2} + x + 1$
\( \Leftrightarrow \dfrac{{2{x^2} - x - 1 - \left( {1 - x} \right)\left( { - 2{x^2} + x + 1} \right)}}{{1 - x}} \le 0\)\( \Leftrightarrow \dfrac{{2{x^2} - x - 1 - \left( { - 2{x^2} + x + 1 + 2{x^3} - {x^2} - x} \right)}}{{1 - x}} \le 0\)\( \Leftrightarrow \dfrac{{ - 2{x^3} + 5{x^2} - x}}{{1 - x}} \le 0\)\( \Leftrightarrow \dfrac{{x\left( { - 2{x^2} + 5x - 1} \right)}}{{1 - x}} \le 0\)
Cho \(x = 0\); \( - 2{x^2} + 5x - 1 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{5 + \sqrt {17} }}{4}\\x = \dfrac{{5 - \sqrt {17} }}{4}\end{array} \right.\); \(x - 1 = 0 \Leftrightarrow x = 1\)
Lập bảng xét dấu ta có: \(0 \le x \le \dfrac{{5 - \sqrt {17} }}{4} \vee 1 < x \le \dfrac{{5 + \sqrt {17} }}{4}\).
Vì là nghiệm nguyên nên có nghiệm là \(0;2\)
- Nếu \(x < - 1\) thì $\dfrac{{2{x^2} - x - 1}}{{\left| {x + 1} \right| - 2x}} \le - 2{x^2} + x + 1$$ \Leftrightarrow \dfrac{{2{x^2} - x - 1}}{{ - 1 - 3x}} \le - 2{x^2} + x + 1$
\( \Leftrightarrow \dfrac{{2{x^2} - x - 1 - \left( { - 1 - 3x} \right)\left( { - 2{x^2} + x + 1} \right)}}{{ - 1 - 3x}} \le 0\)\( \Leftrightarrow \dfrac{{2{x^2} - x - 1 - \left( {2{x^2} - x - 1 + 6{x^3} - 3{x^2} - 3x} \right)}}{{ - 1 - 3x}} \le 0\)\( \Leftrightarrow \dfrac{{ - 6{x^3} + {x^2} + 3x}}{{ - 1 - 3x}} \le 0\)\( \Leftrightarrow \dfrac{{x\left( { - 6{x^2} + x + 3} \right)}}{{ - 1 - 3x}} \le 0\)
Cho \(x = 0\) ; \( - 6{x^2} + x + 3 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{1 + \sqrt {73} }}{{12}}\\x = \dfrac{{1 - \sqrt {73} }}{{12}}\end{array} \right.\); \( - 3x - 1 = 0\)\( \Leftrightarrow x = - \dfrac{1}{3}\)
Lập bảng xét dấu ta có: \(\dfrac{{1 - \sqrt {73} }}{{12}} \le x < - \dfrac{1}{3} \vee 0 \le x \le \dfrac{{1 + \sqrt {73} }}{{12}}\).
Vì là nghiệm nguyên nên có nghiệm là \(0\)(loại)
Vậy bất phương trình đã cho có 2 nghiệm nguyên.
Cho bất phương trình:\(\left| {{x^2} + x + a} \right| + \left| {{x^2} - x + a} \right| \le 2x\)( 1). Khi đó khẳng định nào sau đây đúng nhất?
Ta có \(\left| {{x^2} + x + a} \right| + \left| {{x^2} - x + a} \right| \le 2x\) \( \Leftrightarrow \left| {{{\left( {x + \dfrac{1}{2}} \right)}^2} + \left( {a - \dfrac{1}{4}} \right)} \right| + \left| {{{\left( {x - \dfrac{1}{2}} \right)}^2} + \left( {a - \dfrac{1}{4}} \right)} \right| \le 2x\)
Do vế trái luôn lớn hơn hoặc bằng \(0\) nên để BPT có nghiệm thì \(2x \ge 0 \Leftrightarrow x \ge 0\) nên B đúng.
Nếu \(a > \dfrac{1}{4}\) thì BPT \( \Leftrightarrow 2{x^2} - 2x + 2a \le 0\) vô nghiệm hay BPT có nghiệm khi \(a \le \dfrac{1}{4}\) nên A đúng.
Khi \(a < 0\) ta có \({x^2} + x + a = 0,{x^2} - x + a = 0\) có 4 nghiệm xếp thứ tự \({x_1} < {x_2} < {x_3} < {x_4}\)
Với \(x > {x_4}\) hoặc \(x < {x_1}\) ta có BPT: \(2{x^2} - 2x + 2a \le 0\)
Có nghiệm \({x_1} < x < {x_2}\) và \({x_1} + {x_2} = 1;{x_1}{x_2} < 0\)
Nên tồn tại nghiệm lớn hơn 1 vậy C đúng
Hệ bất phương trình $\left\{ \begin{array}{l}\left( {x + 3} \right)\left( {4 - x} \right) > 0\left( 1 \right)\\x < m - 1\left( 2 \right)\end{array} \right.$ có nghiệm khi và chỉ khi:
Bất phương trình \(\left( 1 \right) \Leftrightarrow - 3 < x < 4.\) Suy ra \({S_1} = \left( { - 3;4} \right)\).
Bất phương trình có \({S_2} = \left( { - \infty ;m - 1} \right).\)
Hệ bất phương trình có nghiệm khi và chỉ khi \({S_1} \cap {S_2} \ne \emptyset \) \( \Leftrightarrow m - 1 > - 3 \Leftrightarrow m > - 2.\)
Phương trình $\left( {m + 1} \right){x^2} - 2\left( {m - 1} \right)x + {m^2} + 4m - 5 = 0$có đúng hai nghiệm ${x_1},{x_2}$ thoả $2 < {x_1} < {x_2}$. Hãy chọn kết quả đúng trong các kết quả sau
Để phương trình $\left( {m + 1} \right){x^2} - 2\left( {m - 1} \right)x + {m^2} + 4m - 5 = 0$ có có đúng hai nghiệm ${x_1},{x_2}$ thoả $2 < {x_1} < {x_2}$.
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\m + 1 \ne 0\\{x_2} > {x_1} > 2\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 1} \right)^2} - \left( {m + 1} \right)\left( {{m^2} + 4m - 5} \right) > 0\\m \ne - 1\\\left( {{x_1} - 2} \right) + \left( {{x_2} - 2} \right) > 0\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) > 0\end{array} \right.$.
Theo Vi-et ta có $\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{2\left( {m - 1} \right)}}{{m + 1}}\\{x_1}.{x_2} = \dfrac{{{m^2} + 4m - 5}}{{m + 1}}\end{array} \right.$.
$ \Rightarrow \left\{ \begin{array}{l}\left( {m - 1} \right)\left( { - {m^2} - 5m - 6} \right) > 0\\m \ne - 1\\\dfrac{{2\left( {m - 1} \right)}}{{m + 1}} - 4 > 0\\\dfrac{{{m^2} + 4m - 5}}{{m + 1}} - 2.\dfrac{{2\left( {m - 1} \right)}}{{m + 1}} + 4 > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l} - 2 < m < 1\\m < - 3\end{array} \right.\\m \ne - 1\\ - 3 < m < - 1\\m > - 3\end{array} \right.$$ \Leftrightarrow - 2 < m < - 1$.
Có bao nhiêu giá trị thực của m để hệ \(\left\{ \begin{array}{l}{x^2} - 2\left( {m + 1} \right)x + {m^2} + 1 \le 0\\{x^2} - 6x + 5 \le 0\end{array} \right.\) có tập nghiệm là một đoạn có độ dài \(\dfrac{3}{2}\)
\(\left\{ \begin{array}{l}{x^2} - 2\left( {m + 1} \right)x + {m^2} + 1 \le 0\\{x^2} - 6x + 5 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 2\left( {m + 1} \right)x + {m^2} + 1 \le 0(1)\\1 \le x \le 5(2)\end{array} \right.\)
\({S_2} = \left[ {1;5} \right]\) là tập nghiệm của (2)
Ta có \({\Delta _{(1)}}' = {\left( {m + 1} \right)^2} - {m^2} - 1 = 2m\)
(1) có nghiệm \( \Leftrightarrow {\Delta _{(1)}}' \ge 0 \Leftrightarrow m \ge 0\)
Khi đó (1)\( \Leftrightarrow m + 1 - \sqrt {2m} \le x \le m + 1 + \sqrt {2m} \)\( \Rightarrow {S_1} = \left[ {m + 1 - \sqrt {2m} ;m + 1 + \sqrt {2m} } \right]\) là tập nghiệm của (1).
\( \Rightarrow S = {S_1} \cap {S_2}\) là tập nghiệm của hệ.
\( \Rightarrow S \subset {S_1}\) và \(S \subset {S_2}\).
Mà S là đoạn có độ dài bằng \(\dfrac{3}{2}\) nên ta chỉ cần xét 2 trường hợp: trường hợp \({S_1}\) có độ dài lớn hơn \(\dfrac{3}{2}\) và trường hợp đoạn \({S_1}\) có độ dài bằng \(\dfrac{3}{2}\).
Trường hợp 1: Đoạn \(\left[ {m + 1 - \sqrt {2m} ;m + 1 + \sqrt {2m} } \right]\) có độ dài lớn hơn \(\dfrac{3}{2}\). Tức là,
\(\begin{array}{l}\left( {m + 1 + \sqrt {2m} } \right) - \left( {m + 1 - \sqrt {2m} } \right) > \dfrac{3}{2}\\ \Leftrightarrow 2\sqrt {2m} > \dfrac{3}{2} \Leftrightarrow m > \dfrac{9}{{32}}\end{array}\)
Khi đó \(S = {S_1} \cap {S_2}\) chỉ có thể là \(\left[ {1;m + 1 + \sqrt {2m} } \right]\) hoặc \(\left[ {m + 1 - \sqrt {2m} ;5} \right]\).
\( + )S = \left[ {1;m + 1 + \sqrt {2m} } \right] \Leftrightarrow m + 1 + \sqrt {2m} - 1 = \dfrac{3}{2}\)
\(\begin{array}{l} \Leftrightarrow m + \sqrt {2m} - \dfrac{3}{2} = 0\\ \Leftrightarrow 2m + 2\sqrt {2m} - 3 = 0\\ \Leftrightarrow \sqrt {2m} = 1 \Leftrightarrow m = \dfrac{1}{2}(TM)\end{array}\)
\( + )S = \left[ {m + 1 - \sqrt {2m} ;5} \right]\)
\(\begin{array}{l} \Leftrightarrow 5 - m - 1 + \sqrt {2m} = \dfrac{3}{2}\\ \Leftrightarrow m - \sqrt {2m} - \dfrac{5}{2} = 0\\ \Leftrightarrow 2m - 2\sqrt {2m} - 5 = 0\\ \Leftrightarrow \sqrt {2m} = 1 + \sqrt 6 \\ \Leftrightarrow m = \dfrac{{7 + 2\sqrt 6 }}{2}(TM)\end{array}\)
Trường hợp 2: Đoạn \(\left[ {m + 1 - \sqrt {2m} ;m + 1 + \sqrt {2m} } \right]\) có độ dài có độ dài bằng \(\dfrac{3}{2}\). Tức là, \(S = \left[ {m + 1 - \sqrt {2m} ;m + 1 + \sqrt {2m} } \right]\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\left( {m + 1 + \sqrt {2m} } \right) - \left( {m + 1 - \sqrt {2m} } \right) = \dfrac{3}{2}\\m + 1 - \sqrt {2m} \ge 1\\m + 1 + \sqrt {2m} \le 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2\sqrt {2m} = \dfrac{3}{2}\\m + 1 - \sqrt {2m} \ge 1\\m + 1 + \sqrt {2m} \le 5\end{array} \right.\end{array}\)
\( \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{9}{{32}}\\m + 1 - \sqrt {2m} \ge 1\\m + 1 + \sqrt {2m} \le 5\end{array} \right.\) (Loại)
Vậy có 2 giá trị của m thỏa mãn.
Tập nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}{x^2} + 6x + 5 > 0\\{x^2} + x - 6 < 0\end{array} \right.\) là
\(\left\{ \begin{array}{l}{x^2} + 6x + 5 > 0\\{x^2} + x - 6 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x + 1} \right)\left( {x + 5} \right) > 0\\\left( {x - 2} \right)\left( {x + 3} \right) < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x > - 1\\x < - 5\end{array} \right.\\ - 3 < x < 2\end{array} \right. \Leftrightarrow - 1 < x < 2.\)
Để phương trình sau có nghiệm duy nhất: $\left| {2{x^2} - 3x - 2} \right| = 5a - 8x - {x^2}$ thì giá trị của tham số $a$ là:
TH1: \(2{x^2} - 3x - 2 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - \dfrac{1}{2}\end{array} \right.\)
Khi đó
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow 2{x^2} - 3x - 2 = 5a - 8x - {x^2}\\ \Leftrightarrow 3{x^2} + 5x - 2 = 5a\end{array}\)
TH2: \(2{x^2} - 3x - 2 < 0 \Leftrightarrow - \dfrac{1}{2} < x < 2\)
Khi đó
\(\begin{array}{l}\left( 1 \right) \Leftrightarrow - 2{x^2} + 3x + 2 = 5a - 8x - {x^2}\\ \Leftrightarrow - {x^2} + 11x + 2 = 5a\end{array}\)
Suy ra \(5a = \left\{ \begin{array}{l}3{x^2} + 5x - 2\,khi\,x \ge 2\,hoac\,x \le - \dfrac{1}{2}\\ - {x^2} + 11x + 2\,khi\, - \dfrac{1}{2} < x < 2\end{array} \right.\)
Xét hàm \(f\left( x \right) = \left\{ \begin{array}{l}3{x^2} + 5x - 2\,khi\,x \ge 2\,hoac\,x \le - \dfrac{1}{2}\\ - {x^2} + 11x + 2\,khi\, - \dfrac{1}{2} < x < 2\end{array} \right.\) ta có:
Với \(x \in \left( { - \infty ; - \dfrac{1}{2}} \right] \cup \left[ {2; + \infty } \right)\) thì \(f\left( x \right) = 3{x^2} + 5x - 2\) có:
\( - \dfrac{b}{{2a}} = - \dfrac{5}{6}\) và \(a = 3 > 0\) nên hàm số đống biến trên \(\left( { - \dfrac{5}{6}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \dfrac{5}{6}} \right)\).
Kết hợp với tập đang xét \(x \in \left( { - \infty ; - \dfrac{1}{2}} \right] \cup \left[ {2; + \infty } \right)\) ta được hàm số đồng biến trên các khoảng \(\left( { - \dfrac{5}{6}; - \dfrac{1}{2}} \right)\) và \(\left( {2; + \infty } \right)\), hàm số nghịch biên trên \(\left( { - \infty ; - \dfrac{5}{6}} \right)\).
Với \(x \in \left( { - \dfrac{1}{2};2} \right)\) thì \(f\left( x \right) = - {x^2} + 11x + 2\) có:
\( - \dfrac{b}{{2a}} = \dfrac{{11}}{2}\) và \(a = - 1 < 0\) nên hàm số đồng biến trên \(\left( { - \infty ;\dfrac{{11}}{2}} \right)\) và nghịch biến trên \(\left( {\dfrac{{11}}{2}; + \infty } \right)\)
Kết hợp với khoảng đang xét \(\left( { - \dfrac{1}{2};2} \right)\) ta được hàm số đồng biến trên \(\left( { - \dfrac{1}{2};2} \right)\).
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: phương trình (1) có nghiệp duy nhất \(5a = - \dfrac{{49}}{{12}} \Leftrightarrow a = -\dfrac{{ 49}}{{60}}\).
Bất phương trình \(\sqrt {\left( {x + 5} \right)\left( {3x + 4} \right)} > 4\left( {x - 1} \right)\) có bao nhiêu nghiệm nguyên lớn hơn -8
TXĐ: \(D = \left( { - \infty ; - 5} \right] \cup \left[ { - \dfrac{4}{3}; + \infty } \right)\)
TH1: \(x - 1 < 0 \Leftrightarrow x < 1\). Kết hợp với điều kiện ta được \(x \in \left( { - \infty ; - 5} \right]\)
TH2:
\(\begin{array}{l}\sqrt {\left( {x + 5} \right)\left( {3x + 4} \right)} > 4\left( {x - 1} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\3{x^2} + 19x + 20 > 16\left( {{x^2} - 2x + 1} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\13{x^2} - 51x - 4 < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\ - \dfrac{1}{{13}} < x < 4\end{array} \right. \Leftrightarrow 1 \le x < 4\end{array}\)
\(S = \left( { - \infty ; - 5} \right] \cup {\rm{[}}1;4)\)
Vậy có 6 nghiệm nguyên lớn hơn -8 là :-7;-6;-5;1;2;3.
Phương trình $\left| {x - 2} \right|\left( {x + 1} \right) + m = 0$ có ba nghiệm phân biệt, giá trị thích hợp của tham số $m$ là:
Xét $\left| {x - 2} \right|\left( {x + 1} \right) + m = 0 \left( 1 \right)$
Với \(x \ge 2\), ta có: \(\left( 1 \right) \Leftrightarrow \left( {x - 2} \right)\left( {x + 1} \right) + m = 0\) \( \Leftrightarrow m = - {x^2} + x + 2\)
Với \(x < 2\), ta có: \(\left( 1 \right) \Leftrightarrow - \left( {x - 2} \right)\left( {x + 1} \right) + m = 0\) \( \Leftrightarrow m = {x^2} - x - 2\)
Đặt \(f\left( x \right) = \left\{ \begin{array}{l} - {x^2} + x + 2{\rm{ }} & {\rm{khi }}x \ge 2\\{x^2} - x - 2{\rm{ }} & {\rm{khi }}x < 2\end{array} \right.\)
Bảng biến thiên:
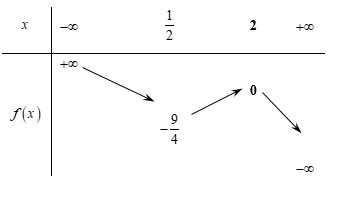
Dựa vào bảng biến thiên ta có \( - \dfrac{9}{4} < m < 0\).
Tập nghiệm của bất phương trình \(\dfrac{{x - 3}}{{x + 1}} > \dfrac{{x + 4}}{{x + 2}}\) là
Điều kiện xác định: \(x \ne - 1,x \ne - 2.\)
\(\begin{array}{l}\dfrac{{x - 3}}{{x + 1}} > \dfrac{{x + 4}}{{x + 2}} \Leftrightarrow \dfrac{{x - 3}}{{x + 1}} - \dfrac{{x + 4}}{{x + 2}} > 0\\ \Leftrightarrow \dfrac{{\left( {x - 3} \right)\left( {x + 2} \right) - \left( {x + 4} \right)\left( {x + 1} \right)}}{{\left( {x + 1} \right)\left( {x + 2} \right)}} > 0\\ \Leftrightarrow \dfrac{{{x^2} - x - 6 - {x^2} - 5x - 4}}{{\left( {x + 1} \right)\left( {x + 2} \right)}} > 0\\ \Leftrightarrow \dfrac{{ - 6x - 10}}{{\left( {x + 1} \right)\left( {x + 2} \right)}} > 0 \Leftrightarrow \dfrac{{3x + 5}}{{\left( {x + 1} \right)\left( {x + 2} \right)}} < 0\end{array}\)
Ta có bảng xét dấu:
Dựa vào BXD ta thấy bất phương trình có tập nghiệm là: \(S = \left( { - \infty ;\, - 2} \right) \cup \left( { - \dfrac{5}{3}; - 1} \right).\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới.

Hỏi có tất cả bao nhiêu giá trị nguyên dương của tham số \(m\) để bất phương trình \(f\left( { - {x^2} + 4x} \right) > m\) có nghiệm thuộc khoảng \(\left( {0;3} \right)\)?
Đặt \(t = - {x^2} + 4x\) với \(x \in \left( {0;3} \right)\)
Bảng biến thiên:

Suy ra \(0 < t \le 4.\)
Khi đó, bất phương trình trở thành:
\(f\left( t \right) > m\,\,\left( 1 \right)\)
Vẽ đồ thị \(\left( C \right)\) của hàm số \(y = f\left( t \right)\) ứng với \(t \in \left( {0;4} \right]\).

Bất phương trình đã cho có nghiệm thuộc khoảng \(\left( {0;3} \right) \Leftrightarrow \left( 1 \right)\) có nghiệm thuộc nửa khoảng \(\left( {0;4} \right]\)\( \Leftrightarrow \) phần đồ thị của hàm số \(y = f\left( t \right)\) với \(t \in \left( {0;4} \right]\) nằm phía trên đường thẳng \(d:y = m\)\( \Leftrightarrow m < 8.\)
Vậy số các giá trị nguyên dương của tham số \(m\) là \(7.\)
Tập nghiệm của bất phương trình \({x^2} + 5x - 6 \le 0\) là:
\({x^2} + 5x - 6 \le 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 6} \right) \Leftrightarrow 0 \Leftrightarrow - 6 \le x \le 1\)
Vậy tập nghiệm của BPT là: \(\left[ { - 6;1} \right].\)
\({x^2} + 5x - 6 \le 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 6} \right) \Leftrightarrow 0 \Leftrightarrow - 6 \le x \le 1\)
Vậy tập nghiệm của BPT là: \(\left[ { - 6;1} \right].\)
Tìm \(m\) để hệ bất phương trình \(\left\{ \begin{array}{l} - {x^2} + 5x - 4 \ge 0\\{x^2} - \left( {m - 1} \right)x - m \le 0\end{array} \right.\) có nghiệm duy nhất.
\(\left\{ \begin{array}{l} - {x^2} + 5x - 4 \ge 0\\{x^2} - \left( {m - 1} \right)x - m \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {x - 4} \right) \le 0\\\left( {x + 1} \right)\left( {x - m} \right) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 4\\\left( {x + 1} \right)\left( {x - m} \right) \le 0\end{array} \right.\,\,\left( I \right)\)
+) Nếu \(x - m \ge x + 1 \Leftrightarrow m \le - 1\) thì \(\left( I \right) \Leftrightarrow \) \(\left\{ \begin{array}{l}1 \le x \le 4\\x + 1 \le 0\\x - m \ge 0\end{array} \right.\, \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 4\\m \le x \le - 1\end{array} \right.,\) hệ vô nghiệm.
+) Nếu \(x - m < x + 1 \Leftrightarrow m > - 1\) thì \(\left( I \right) \Leftrightarrow \)\(\left\{ \begin{array}{l}1 \le x \le 4\\x + 1 \ge 0\\x - m \le 0\end{array} \right.\, \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 4\\ - 1 \le x \le m\end{array} \right..\)
Vậy hệ bất phương trình có nghiệm duy nhất khi và chỉ khi \(m = 1.\)
Bất phương trình \((x - 1)(3{x^2} + 7x + 4) \le 0\) có tập nghiệm là:
\((x - 1)(3{x^2} + 7x + 4) \le 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 1} \right)\left( {3x + 4} \right) \le 0\)
Đặt \(f\left( x \right) = \left( {x - 1} \right)\left( {3{x^2} + 7x + 4} \right)\) .
Xét phương trình : \(3{x^2} + 7x + 4 = 0 \Leftrightarrow \left( {x + 1} \right)\left( {3x + 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - \dfrac{4}{3}\end{array} \right..\) Ta có bảng:
Vậy \(f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \infty ; - \dfrac{4}{3}} \right] \cup \left[ { - 1;1} \right]\)
\(\dfrac{{2x + 1}}{{2{x^2} - 3x + 1}} \ge 0 \Leftrightarrow \dfrac{{2x + 1}}{{\left( {2x - 1} \right)\left( {x - 1} \right)}} \ge 0\)
ĐKXĐ: \(\left\{ \begin{array}{l}x \ne 1\\x \ne \dfrac{1}{2}\end{array} \right.\)
Đặt \(f\left( x \right) = \dfrac{{2x + 1}}{{2{x^2} - 3x + 1}}\) . Ta có bảng:
Vậy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \left[ { - \dfrac{1}{2};\dfrac{1}{2}} \right) \cup \left( {1; + \infty } \right)\)
\(\left| {{x^2} + 3x - 4} \right| < x - 8 \)\(\Leftrightarrow \left\{ \begin{array}{l}x - 8 > 0\\8 - x < {x^2} + 3x - 4\\{x^2} + 3x - 4 < x - 8\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x > 8\\{x^2} + 4x - 12 > 0\\{x^2} + 2x + 4 < 0\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x > 8\\\left( {x - 2} \right)\left( {x + 6} \right) > 0\\{\left( {x + 1} \right)^2} + 3 < 0\,\,\,\,\left( {VN} \right)\end{array} \right.\)
Vậy bất phương trình vô nghiệm.
Tập nghiệm của bất phương trình \(\sqrt {{x^2} - 4x - 21} \le x - 3\) là:
\(\begin{array}{l}\,\,\,\,\sqrt {{x^2} - 4x - 21} \le x - 3 \\\Leftrightarrow \left\{ \begin{array}{l}{x^2} - 4x - 21 \ge 0\\x - 3 \ge 0\\{x^2} - 4x - 21 \le {x^2} - 6x + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left( {x + 3} \right)\left( {x - 7} \right) \ge 0\\x \ge 3\\2x \le 30\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \le - 3\\x \ge 7\end{array} \right.\\x \ge 3\\x \le 15\end{array} \right. \Leftrightarrow 7 \le x \le 15\end{array}\)
Vậy tập nghiệm của BPT là: \(S = \left[ {7;15} \right].\)

