Tập nghiệm của bất phương trình \(\left( {4 - {x^2}} \right)\sqrt {2 - x} < 0\) là
Điều kiện xác định: \(x \le 2.\)
\(\left( {4 - {x^2}} \right)\sqrt {2 - x} < 0 \Leftrightarrow \left( {2 + x} \right)\left( {2 - x} \right)\sqrt {2 - x} < 0\)\( \Leftrightarrow \left\{ \begin{array}{l}2 - x > 0\\2 + x < 0\end{array} \right. \Leftrightarrow x < - 2.\)
ĐKXĐ: \( - 2 \le x \le 4\)
\(\begin{array}{l}\,\,\,\,\,\,{x^2} + m + 4\sqrt {(x + 2)(4 - x)} \ge 2x + 18\\ \Leftrightarrow - {x^2} + 2x + 8 - 4\sqrt { - {x^2} + 2x + 8} + 10 \le m\end{array}\)
Đặt \(\sqrt { - {x^2} + 2x + 8} = t\,\,\,\,\,\,\,\left( {t \ge 0} \right)\)
Ta có: \( - {x^2} + 2x + 8 = - {\left( {x - 1} \right)^2} + 9 \le 9\) với mọi \(x \in \left[ { - 2;4} \right]\)
\( \Rightarrow 0 \le t \le 3\)
Đề bài trở thành: Tìm m để bất phương trình \({t^2} - 4t + 10 \le m\) có nghiệm thuộc \(\left[ {0;3} \right]\)
\( \Leftrightarrow m \ge \mathop {Max}\limits_{\left[ {0;\,3} \right]} \left( {{t^2} - 4t + 10} \right)\)
Xét \(f\left( t \right) = {t^2} - 4t + 10\) ta có bảng biến thiên
Vậy để bất phương trình \({t^2} - 4t + 10 \le m\) có nghiệm thuộc \(\left[ {0;3} \right]\) \( \Leftrightarrow m \ge 10.\)
Tập nghiệm của bất phương trình \( - {x^2} + 6x + 7 \ge 0\) là
Giải: \(f\left( x \right) = - {x^2} + 6x + 7 = 0\)\( \Leftrightarrow \left( {x + 1} \right)\left( {x - 7} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 7\end{array} \right.\)
Ta có bảng xét dấu:
![]()
Vậy bất phương trình có tập nghiệm \(S = \left[ { - 1;\,\,7} \right]\).
Bất phương trình \({x^2} - 6\sqrt 2 x + 18 \ge 0\) có tập nghiệm là:
Theo đề bài, ta có:
\(\begin{array}{l}{x^2} - 6\sqrt 2 x + 18 \ge 0\\ \Leftrightarrow {x^2} - 2.3\sqrt 2 .x + {\left( {3\sqrt 2 } \right)^2} \ge 0\\ \Leftrightarrow {\left( {x - 3\sqrt 2 } \right)^2} \ge 0\,\,\,\left( 1 \right)\end{array}\)
Bất đẳng thức \(\left( 1 \right)\) luôn đúng với mọi \(x \in \mathbb{R}\).
Vậy \(S = \mathbb{R}\).
Gọi m và M lần lượt là nghiệm nguyên nhỏ nhất và lớn nhất của hệ bất phương trình \(\left\{ \begin{array}{l}{\left( {2 - x} \right)^2} \le 7 - 3x + {x^2}\\{\left( {x + 2} \right)^3} < {x^3} + 3{x^2} + 3x + 20\end{array} \right.\). Tổng \(m + M\) bằng:
\(\begin{array}{l}\left\{ \begin{array}{l}{\left( {2 - x} \right)^2} \le 7 - 3x + {x^2}\\{\left( {x + 2} \right)^3} < {x^3} + 3{x^2} + 3x + 20\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4 - 4x + {x^2} \le 7 - 3x + {x^2}\\{x^3} + 6{x^2} + 12x + 8 < {x^3} + 3{x^2} + 3x + 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + 3 \ge 0\\3{x^2} + 9x - 12 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 3\\ - 4 < x < 1\end{array} \right. \Leftrightarrow - 3 \le x < 1\\ \Rightarrow \left\{ \begin{array}{l}m = - 3\\M = 0\end{array} \right. \Rightarrow m + M = - 3.\end{array}\)
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \( - 2{x^2} + 2\left( {m - 2} \right)x + m - 2 \ge 0\) có nghiệm.
Đặt \(f\left( x \right) = - 2{x^2} + 2\left( {m - 2} \right)x + m - 2\).
\(\Delta ' = {\left( {m - 2} \right)^2} + 2\left( {m - 2} \right) = {m^2} - 2m\)
+) \(\left\{ \begin{array}{l}a = - 2 < 0\\\Delta ' < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = - 2 < 0\\{m^2} - 2m < 0\end{array} \right.\)\( \Leftrightarrow 0 < m < 2\)
\( \Rightarrow f\left( x \right) < 0,\,\,\forall x \in \mathbb{R}\)
Vậy bất phương trình \( - 2{x^2} + 2\left( {m - 2} \right)x + m - 2 \ge 0\) vô nghiệm.
\( \Rightarrow \) Loại
+) \(\Delta ' = 0 \Leftrightarrow {m^2} - 2m = 0\)\( \Leftrightarrow m\left( {m - 2} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\)
\( \Rightarrow f\left( x \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l} - 2{x^2} - 4x - 2 = 0\\ - 2{x^2} = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\end{array} \right.\) (thỏa mãn)
Vậy bất phương trình \( - 2{x^2} + 2\left( {m - 2} \right)x + m - 2 \ge 0\) có nghiệm \(\left[ \begin{array}{l}x = - 1\\x = 0\end{array} \right.\).
\( \Rightarrow \) Nhận \(m = 0;\,\,m = 2\).
+) \(\Delta ' > 0\)\( \Leftrightarrow {m^2} - 2m > 0\)\( \Leftrightarrow m\left( {m - 2} \right) > 0\)\( \Leftrightarrow \left[ \begin{array}{l}m < 0\\m > 2\end{array} \right.\)
\( \Rightarrow f\left( x \right) = 0\) có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) (giả sử \({x_1} < {x_2}\))
Bảng xét dấu:

Dựa vào bảng xét dấu, ta có: \(f\left( x \right) \ge 0 \Leftrightarrow {x_1} \le x \le {x_2}\)
\( \Rightarrow \) Nhận \(\left[ \begin{array}{l}m < 0\\m > 2\end{array} \right.\)
Kết hợp các trường hợp, ta được \(m \in \left( { - \infty ;\,\,0} \right] \cup \left[ {2;\,\, + \infty } \right)\).
Vậy \(m \in \left( { - \infty ;\,0} \right] \cup \left[ {2;\, + \infty } \right)\).
Số nghiệm của bất phương trình \(\sqrt {{x^2} - 2x} \le \sqrt 3 \) là:
ĐKXĐ: \({x^2} - 2x \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le 0\\x \ge 2\end{array} \right.\)
\(\sqrt {{x^2} - 2x} \le \sqrt 3 \Leftrightarrow {x^2} - 2x \le 3 \Leftrightarrow {x^2} - 2x - 3 \le 0 \Leftrightarrow - 1 \le x \le 3\)
Kết hợp ĐKXĐ \( \Rightarrow x \in \left[ { - 1;0} \right] \cup \left[ {2;3} \right]\)
Vậy BPT có 4 nghiệm nguyên.
Tập nghiệm của bất phương trình \(\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1\) là
Điều kiện: \(x \ne \pm 2\)
Ta có:
\(\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1 \Leftrightarrow \dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} - 1 \ge 0\)
\( \Leftrightarrow \dfrac{{x + 1}}{{{x^2} - 4}} \ge 0\)(*)
Bảng xét dấu:
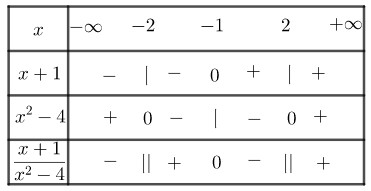
Từ bảng xét dấu, bất phương trình
(*)\( \Leftrightarrow x \in \left( { - 2; - 1} \right] \cup \left( {2; + \infty } \right)\)
Tìm m để hệ \(\left\{ \begin{array}{l}{x^2} - 2\left( {m + 2} \right)x - 2m - 5 > 0\\2{x^2} + \left( {m + 9} \right)x + m + 7 > 0\end{array} \right.\) đúng với mọi \(x\).
\(\left\{ \begin{array}{l}{x^2} - 2\left( {m + 2} \right)x - 2m - 5 > 0(1)\\2{x^2} + \left( {m + 9} \right)x + m + 7 > 0(2)\end{array} \right.\) đúng với mọi \(x\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{\Delta _{(1)}}' < 0\\{\Delta _{(2)}} < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 2} \right)^2} + 2m + 5 < 0\\{\left( {m + 9} \right)^2} - 8\left( {m + 7} \right) < 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 3} \right)^2} < 0\\{\left( {m + 5} \right)^2} < 0\end{array} \right. \Leftrightarrow m \in \emptyset \end{array}\)
Tập nghiệm của bất phương trình \(2{x^2} + x + 1 > 0\) là:
\(2{x^2} + x + 1 > 0 \Leftrightarrow {\left( {\sqrt 2 x + \dfrac{{\sqrt 2 }}{4}} \right)^2} + \dfrac{7}{8} > 0\) luôn đúng với \(\forall x\)
Vậy tập nghiệm của BPT là R.
Giải bất phương trình \( - 2{x^2} + 3x - 7 \ge 0.\)
Ta có $-2{x^2} + 3x - 7\; = 0$ vô nghiệm.
Bảng xét dấu
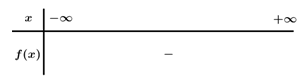
Dựa vào bảng xét dấu $ - 2{x^2} + 3x - 7 \ge 0\, \Leftrightarrow \,x \in \emptyset $.
Tập nghiệm của bất phương trình \(\left| {2x + 1} \right| < x + 2\) là:
\(\left| {2x + 1} \right| < x + 2 \Leftrightarrow \left\{ \begin{array}{l}x + 2 > 0\\{\left( {2x + 1} \right)^2} < {\left( {x + 2} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - 2\\4{x^2} + 4x + 1 < {x^2} + 4x + 4\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x > - 2\\3{x^2} - 3 < 0\end{array} \right. \)\(\Leftrightarrow \left\{ \begin{array}{l}x > - 2\\ - 1 < x < 1\end{array} \right. \Leftrightarrow - 1 < x < 1\)
Vậy tập nghiệm của BPT là \(\left( { - 1;1} \right).\)
\({x^2} - 16 \le 0 \Leftrightarrow {x^2} \le 16 \Leftrightarrow - 4 \le x \le 4 \Leftrightarrow \left\{ \begin{array}{l}x + 4 \ge 0\\x - 4 \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x + 4} \ge 0\\x - 4 \le 0\end{array} \right. \Leftrightarrow \sqrt {x + 4} \left( {x - 4} \right) \le 0\)
Tập nghiệm của bất phương trình \(\dfrac{{{x^2} + 2x - 8}}{{\left| {x + 1} \right|}} < 0\) là:
\(\dfrac{{{x^2} + 2x - 8}}{{\left| {x + 1} \right|}} < 0\) ĐKXĐ: \(x \ne - 1\)
\( \Rightarrow {x^2} + 2x - 8 < 0\) (do \(\left| {x + 1} \right| > 0\) với \(\forall x \ne - 1\))
\( \Leftrightarrow - 4 < x < 2\) . Kết hợp ĐKXĐ \( \Rightarrow \) tập nghiệm của BPT là \(\left( { - 4; - 1} \right) \cup \left( { - 1;2} \right)\)
Chủ một rạp chiếu phim ước tính, nếu giá mỗi vé xem phim là \(x\) (ngàn đồng) thì lợi nhuận bán vé được tính theo công thức \(P\left( x \right) = - 50{x^2} + 3500x - 2500\)(ngàn đồng). Hỏi muốn lợi nhuận bán vé tối thiểu là 50 triệu đồng thì giá tiền mỗi vé là bao nhiêu?
Lợi nhuận bán vé tối thiểu là 50 triệu đồng
\(\begin{array}{l} \Leftrightarrow P\left( x \right) = - 50{x^2} + 3500x - 2500 \ge 50000\\ \Leftrightarrow - 50{x^2} + 3500x - 52500 \ge 0\\ \Leftrightarrow 35 - 5\sqrt 7 \le x \le 35 + 5\sqrt 7 \end{array}\)
Vậy giá tiền mỗi vé là \(22 \le x \le 48\) ngàn đồng thỏa mãn yêu cầu đề bài.
\( - {x^2} + 5x + 6 > 0 \Leftrightarrow - \left( {x + 1} \right)\left( {x - 6} \right) > 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) < 0 \Leftrightarrow - 1 < x < 6.\)
Vậy tập nghiệm của BPT là \(\left( { - 1;6} \right).\)
Bất phương trình \(({x^2} - x - 6)\sqrt {{x^2} - x - 2} \ge 0\) có tập nghiệm là
ĐKXĐ: \({x^2} - x - 2 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - 1\end{array} \right.\)
\(\left( {{x^2} - x - 6} \right)\sqrt {{x^2} - x - 2} \ge 0\)\( \Leftrightarrow \left( {x + 2} \right)\left( {x - 3} \right)\sqrt {\left( {x - 2} \right)\left( {x + 1} \right)} \ge 0\)
Đặt \(f\left( x \right) = \left( {{x^2} - x - 6} \right)\sqrt {{x^2} - x - 2} \) . Ta có bảng:
Vậy \(f\left( x \right) \ge 0\) \( \Leftrightarrow x \in \left( { - \infty ; - 2} \right] \cup \left[ {3; + \infty } \right) \cup \left\{ { - 1;2} \right\}\)
Tập nghiệm của bất phương trình \({x^2} - 3x + 2 < 0\) là:
Ta có $f\left( x \right) = {x^2} - 3x + 2 = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.$.
Bảng xét dấu
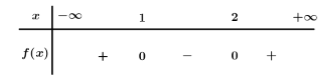
Dựa vào bảng xét dấu \(f\left( x \right) < 0\, \Leftrightarrow \,1 < x < 2\).
Tập nghiệm của bất phương trình \( - {x^2} + 5x - 4 < 0\) là
Ta có $f\left( x \right) = - {x^2} + 5x - 4 = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 1\end{array} \right.$.
Bảng xét dấu
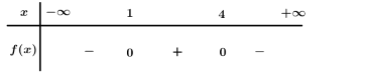
Dựa vào bảng xét dấu \(f\left( x \right) < 0\, \Leftrightarrow \,\left[ \begin{array}{l}x < 1\\x > 4\end{array} \right.\).
Bất phương trình nào sau đây có tập nghiệm là \(\mathbb{R}\)?
Xét \(f\left( x \right) = - 3{x^2} + x - 1\) có \(a = - 3 < 0,\) \(\Delta = {1^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = - 11 < 0\) nên \(f\left( x \right) < 0,\forall x\)
Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\).

