Tập hợp nào dưới đây chứa phần tử không là nghiệm của bất phương trình $\sqrt 2 {x^2} - \left( {\sqrt 2 + 1} \right)x + 1 < 0$?
Ta có $f\left( x \right) = \sqrt 2 {x^2} - \left( {\sqrt 2 + 1} \right)x + 1 = 0$ $ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{\sqrt 2 }}{2}\\x = 1\end{array} \right.$
Bảng xét dấu
Dựa vào bảng xét dấu \(f\left( x \right) < 0\, \Leftrightarrow \dfrac{{\sqrt 2 }}{2} < x < 1\) hay tập nghiệm của bất phương trình là \(\left( {\dfrac{{\sqrt 2 }}{2};1} \right)\).
Quan sát các đáp án ta thấy tập hợp ở đáp án C chứa hai phần tử \(\dfrac{{\sqrt 2 }}{2}\) và \(1\) không thuộc tập nghiệm của bất phương trình đã cho.
Biểu thức \(\left( {3{x^2} - 10x + 3} \right)\left( {4x - 5} \right)\) âm khi và chỉ khi
Đặt $f\left( x \right) = \left( {3{x^2} - 10x + 3} \right)\left( {4x - 5} \right)$
Phương trình \(3{x^2} - 10x + 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 3}\\{x = \dfrac{1}{3}}\end{array}} \right.\) và \(4x - 5 = 0 \Leftrightarrow x = \dfrac{5}{4}.\)
Lập bảng xét dấu
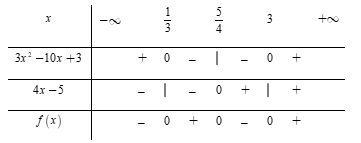
Dựa vào bảng xét dấu, ta thấy $f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,\infty ;\dfrac{1}{3}} \right) \cup \left( {\dfrac{5}{4};3} \right).$
Biểu thức \(\left( {4 - {x^2}} \right)\left( {{x^2} + 2x - 3} \right)\left( {{x^2} + 5x + 9} \right)\) âm khi
Đặt \(f\left( x \right) = \left( {4 - {x^2}} \right)\left( {{x^2} + 2x - 3} \right)\left( {{x^2} + 5x + 9} \right)\)
Phương trình \(4 - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right..\)
Phương trình \({x^2} + 2x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \,3\end{array} \right..\)
Ta có \({x^2} + 5x + 9 = {\left( {x + \dfrac{5}{2}} \right)^2} + \dfrac{{11}}{4} > 0\)
Lập bảng xét dấu:
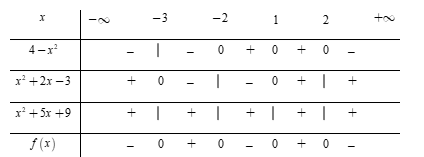
Dựa vào bảng xét dấu ta thấy \(\left( {4 - {x^2}} \right)\left( {{x^2} + 2x - 3} \right)\left( {{x^2} + 5x + 9} \right) < 0\) \( \Leftrightarrow \left[ \begin{array}{l}x < - 3\\ - 2 < x < 1\\x > 2\end{array} \right.\)
\( \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( { - 2;1} \right) \cup \left( {2; + \infty } \right).\)
Tập nghiệm của bất phương trình \({x^3} + 3{x^2} - 6x - 8 \ge 0\) là
Bất phương trình ${x^3} + 3{x^2} - 6x - 8 \ge 0 \Leftrightarrow \left( {x - 2} \right)\left( {{x^2} + 5x + 4} \right) \ge 0.$
Phương trình \({x^2} + 5x + 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - \,4}\\{x = - \,1}\end{array}} \right.\) và \(x - 2 = 0 \Leftrightarrow x = 2.\)
Lập bảng xét dấu
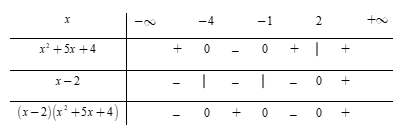
Dựa vào bảng xét dấu, ta thấy rằng $\left( {x - 2} \right)\left( {{x^2} + 5x + 4} \right) \ge 0 \Leftrightarrow x \in \left[ { - \,4; - \,1} \right] \cup \left[ {2; + \,\infty } \right).$
Tập nghiệm của bất phương trình \(2x\left( {2 - x} \right) \ge 2 - x\) là
\(\begin{array}{l}2x\left( {2 - x} \right) \ge 2 - x \Leftrightarrow 2x\left( {x - 2} \right) \le x - 2\\ \Leftrightarrow \left( {x - 2} \right)\left( {2x - 1} \right) \le 0 \Leftrightarrow \dfrac{1}{2} \le x \le 2.\end{array}\)
Tìm \(m\) để \( - 9 < \dfrac{{3{x^2} + mx - 6}}{{{x^2} - x + 1}} < 6\) nghiệm đúng với \(\forall x \in \mathbb{R}\).
Bất phương trình đã cho tương tương với
\( - 9\left( {{x^2} - x + 1} \right) < 3{x^2} + mx - 6 < 6\left( {{x^2} - x + 1} \right)\) (do \({x^2} - x + 1 > 0\forall x \in \mathbb{R}\))
\( \Leftrightarrow \left\{ \begin{array}{l}12{x^2} + \left( {m - 9} \right)x + 3 > 0\,\,\,\left( 1 \right)\\3{x^2} - \left( {m + 6} \right)x + 12 > 0\,\,\,\,\left( 2 \right)\end{array} \right.\)
Yêu cầu \( \Leftrightarrow \) (1) và (2) nghiệm đúng \(\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left\{ \begin{array}{l}{\Delta _{\left( 1 \right)}} < 0\\{\Delta _{\left( 2 \right)}} < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 9} \right)^2} - 144 < 0\\{\left( {m + 6} \right)^2} - 144 < 0\end{array} \right.\) \( \Leftrightarrow - 3 < m < 6\)
Tập nghiệm của hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 7x + 6 < 0\,\,\left( 1 \right)\\\left| {2x - 1} \right| < 3\,\,\left( 2 \right)\end{array} \right.$ là:
Ta có: ${x^2} - 7x + 6 < 0$ \( \Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) < 0\) \( \Leftrightarrow 1 < x < 6\)
Tập nghiệm của $\left( 1 \right)$ là \({S_1} = \left( {1;6} \right).\)
\(\left| {2x - 1} \right| < 3 \Leftrightarrow - 3 < 2x - 1 < 3\) \( \Leftrightarrow - 2 < 2x < 4 \Leftrightarrow - 1 < x < 2\)
Tập nghiệm của $\left( 2 \right)$ là \({S_2} = \left( { - 1;2} \right).\)
Vậy tập nghiệm của hệ là \(S = {S_1} \cap {S_2} = \left( {1;2} \right).\)
Bất phương trình: \(\sqrt {2x + 1} < 3 - x\) có nghiệm là:
Ta có:\(\sqrt {2x + 1} < 3 - x\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{2x + 1 \ge 0}\\{3 - x > 0}\\{2x + 1 < {{\left( {3 - x} \right)}^2}}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge - \dfrac{1}{2}}\\{x < 3}\\{ - {x^2} + 8x - 8 < 0}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge - \dfrac{1}{2}}\\{x < 3}\\{\left[ {\begin{array}{*{20}{c}}{x > 4 + 2\sqrt 2 }\\{x < 4 - 2\sqrt 2 }\end{array}} \right.}\end{array}} \right.\)\( \Leftrightarrow - \dfrac{1}{2} \le x < 4 - 2\sqrt 2 .\)
Hỏi có bao nhiêu giá trị nguyên của $x$ thỏa mãn bất phương trình $\dfrac{{{x^4} - {x^2}}}{{{x^2} + 5x + 6}} \le 0$ ?
Bất phương trình $\dfrac{{{x^4} - {x^2}}}{{{x^2} + 5x + 6}} \le 0$ $ \Leftrightarrow \dfrac{{{x^2}\left( {{x^2} - 1} \right)}}{{{x^2} + 5x + 6}} \le 0\,\,\,\,\,\,\,\left( * \right)$
Vì ${x^2} \ge 0,\,\,\forall x \in \mathbb{R}$ nên bất phương trình
$\left( * \right) \Leftrightarrow \left[ \begin{array}{l}{x^2} = 0\\\dfrac{{{x^2} - 1}}{{{x^2} + 5x + 6}} \le 0\end{array} \right.$ $ \Leftrightarrow \left[ \begin{array}{l}x = 0\\f\left( x \right) = \dfrac{{{x^2} - 1}}{{{x^2} + 5x + 6}} \le 0\end{array} \right.$
Phương trình ${x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \,1\end{array} \right.$ và ${x^2} + 5x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \,2\\x = - \,3\end{array} \right..$
Bảng xét dấu
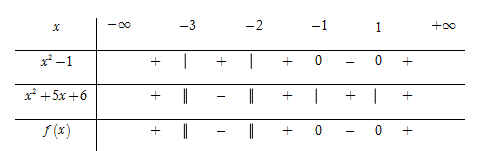
Dựa vào bảng xét dấu, ta thấy $f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,3; - \,2} \right) \cup \left[ { - \,1;1} \right]$
Kết hợp với $x \in \mathbb{Z},$ ta được $x = \left\{ { - \,1;0;1} \right\}.$
Vậy có tất cả $3$ giá trị nguyên cần tìm.
Cho bất phương trình \({x^2} - 8x + 7 \ge 0\). Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.
Ta có $f\left( x \right) = {x^2} - 8x + 7 = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 7\end{array} \right.$.
Bảng xét dấu
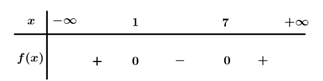
Dựa vào bảng xét dấu \(f\left( x \right) \ge 0\, \Leftrightarrow \,\left[ \begin{array}{l}x \le 1\\x \ge 7\end{array} \right.\).
Tập nghiệm của bất phương trình là \(S = \left( { - \infty ;1} \right] \cup \,\left[ {7; + \infty } \right)\).
Vì \(\dfrac{{13}}{2} \in \left[ {6; + \infty } \right)\) và \(\dfrac{{13}}{2} \notin S\) nên \(\left[ {6; + \infty } \right)\) thỏa yêu cầu bài toán.
Giải bất phương trình $x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right)$ ta được nghiệm:
Bất phương trình $x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right) \Leftrightarrow {x^2} + 5x \le 2{x^2} + 4 \Leftrightarrow {x^2} - 5x + 4 \ge 0$
Xét phương trình ${x^2} - 5x + 4 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right..$
Lập bảng xét dấu:
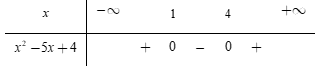
Dựa vào bảng xét dấu, ta thấy nghiệm của bất phương trình ${x^2} - 5x + 4 \ge 0$ là $ x \in \left( { - \,\infty ;1} \right] \cup \left[ {4; + \,\infty } \right).$
Cặp bất phương trình nào sau đây là tương đương?
Đặt $f\left( x \right) = {x^2}\left( {x - 2} \right).$
Phương trình ${x^2} = 0 \Leftrightarrow x = 0$ và $x - 2 = 0 \Leftrightarrow x = 2.$
Lập bảng xét dấu
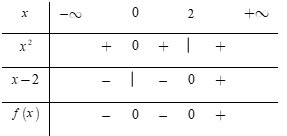
Dựa vào bảng xét dấu ta thấy:
+) Đáp án A: $x - 2 \le 0 \Leftrightarrow x \le 2$ và ${x^2}\left( {x - 2} \right) \le 0 \Leftrightarrow x \le 2$ nên hai bất phương trình tương đương. Chọn A.
+) Đáp án B: $x - 2 < 0 \Leftrightarrow x < 2$ và ${x^2}\left( {x - 2} \right) > 0 \Leftrightarrow x > 2$ nên hai bất phương trình không tương đương. Loại B.
+) Đáp án C: $x - 2 < 0 \Leftrightarrow x < 2$ và ${x^2}\left( {x - 2} \right) < 0 \Leftrightarrow \left\{ \begin{array}{l}x < 2\\x \ne 0\end{array} \right.$ nên hai bất phương trình không tương đương. Loại C.
+) Đáp án D: \({x^2}\left( {x - 2} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x \ge 2\end{array} \right.\) và \(x - 2 \ge 0 \Leftrightarrow x \ge 2\) nên hai bất phương trình không tương đương. Loại D.
Xác định $m$ để với mọi \(x\) ta có \( - 1 \le \dfrac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\).
- Vì \(2{x^2} - 3x + 2 > 0\,\,\forall x \in \mathbb{R}\) nên:
- Bất phương trình \( - 1 \le \dfrac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\) có tập nghiệm là \(\mathbb{R}\) khi hệ sau có tập nghiệm là \(\mathbb{R}\):
$\left\{ \begin{array}{l} - 1\left( {2{x^2} - 3x + 2} \right) \le {x^2} + 5x + m\\{x^2} + 5x + m < 7\left( {2{x^2} - 3x + 2} \right)\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}13{x^2} - 26x + 14 - m > 0\,\,\,\left( 1 \right)\\3{x^2} + 2x + m + 2 \ge 0\,\,\,\,\,\,\,\,\;\left( 2 \right)\end{array} \right.$
- Ta có \(\left( 1 \right)\) có tập nghiệm là \(\mathbb{R}\) khi \(\Delta ' < 0 \Leftrightarrow - 13 + 13m < 0\)\( \Leftrightarrow m < 1\) (3)
- \(\left( 2 \right)\) có tập nghiệm là \(\mathbb{R}\) khi \(\Delta ' \le 0 \Leftrightarrow - 5 - 3m \le 0\)\( \Leftrightarrow m \ge - \dfrac{5}{3}\) (4)
Từ (2) và (4), ta có \( - \dfrac{5}{3} \le m < 1\).
Bất phương trình \(\left( {\left| {x - 1} \right| - 3} \right)\left( {\left| {x + 2} \right| - 5} \right) < 0\) có nghiệm là
Trường hợp 1:\(\left\{ \begin{array}{l}\left| {x - 1} \right| - 3 > 0\\\left| {x + 2} \right| - 5 < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x - 1 > 3\\x - 1 < - 3\end{array} \right.\\ - 5 < x + 2 < 5\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x > 4\\x < - 2\end{array} \right.\\ - 7 < x < 3\end{array} \right.\)\( \Leftrightarrow - 7 < x < - 2\)
Trường hợp 2: \(\left\{ \begin{array}{l}\left| {x - 1} \right| - 3 < 0\\\left| {x + 2} \right| - 5 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 3 < x - 1 < 3\\\left[ \begin{array}{l}x + 2 > 5\\x + 2 < - 5\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l} - 2 < x < 4\\\left[ \begin{array}{l}x > 3\\x < - 7\end{array} \right.\end{array} \right.\)\( \Leftrightarrow 3 < x < 4\)
Bất phương trình:\(\sqrt { - {x^2} + 6x - 5} > 8 - 2x\) có nghiệm là:
Ta có$\sqrt { - {x^2} + 6x - 5} > 8 - 2x$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{ - {x^2} + 6x - 5 \ge 0}\\{8 - 2x < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{8 - 2x \ge 0}\\{ - {x^2} + 6x - 5 > {{\left( {8 - 2x} \right)}^2}}\end{array}} \right.}\end{array}} \right.$$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{1 \le x \le 5}\\{x > 4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 4}\\{ - 5{x^2} + 38x - 69 > 0}\end{array}} \right.}\end{array}} \right.$$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{1 \le x \le 5}\\{x > 4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 4}\\{3 < x < \dfrac{{23}}{5}}\end{array}} \right.}\end{array}} \right.$
\( \Leftrightarrow \left[ \begin{array}{l}
4 < x \le 5\\
3 < x \le 4
\end{array} \right. \Leftrightarrow 3 < x \le 5\)
Tập nghiệm \(S\) của bất phương trình \(\dfrac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le - 1\) là
Điều kiện: \({x^2} - 3x - 10 \ne 0 \Leftrightarrow \left( {x + 2} \right)\left( {x - 5} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne - \,2\\x \ne 5\end{array} \right..\)
Bất phương trình \(\dfrac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le - 1\)\( \Leftrightarrow \dfrac{{ - 2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} + 1 \le 0\) \( \Leftrightarrow \dfrac{{ - {x^2} + 4x - 3}}{{{x^2} - 3x - 10}} \le 0\,\,\,\,\left( * \right)\)
Bảng xét dấu
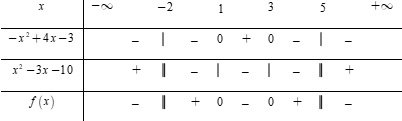
Dựa vào bảng xét dấu, bất phương trình \(\left( * \right) \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left[ {1;3} \right] \cup \left( {5; + \,\infty } \right).\)
Nghiệm của hệ bất phương trình: $\left\{ {\begin{array}{*{20}{c}}{2{x^2} - x - 6 \le 0}\\{{x^3} + {x^2} - x - 1 \ge 0}\end{array}} \right.$là:
Cách giải:
Ta có $2{x^2} - x - 6 \le 0 \Leftrightarrow - \dfrac{3}{2} \le x \le 2,{\rm{ }}\left( I \right)$.
${x^3} + {x^2} - x - 1 \ge 0$$ \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - 1} \right) \ge 0$$ \Leftrightarrow \left( {x - 1} \right){\left( {x + 1} \right)^2} \ge 0$$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 1}\\{x \ge 1}\end{array}} \right..{\rm{ }}\left( {II} \right)$
Từ $\left( I \right)$ và $\left( {II} \right)$ suy ra nghiệm của hệ là $S = \left[ {1;{\rm{ }}2} \right] \cup \left\{ { - 1} \right\}$.
Số nghiệm của phương trình: $\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } $ là:
Điều kiện \(x \ge - 7\).
Đặt \(t = \sqrt {x + 7} \) , điều kiện \(t \ge 0\).
Ta có \(\sqrt {{t^2} + 1 - 2t} = 2 - \sqrt {{t^2} - 6 - t} \)\( \Leftrightarrow \left| {t - 1} \right| = 2 - \sqrt {{t^2} - t - 6} \)
Nếu \(t \ge 1\) thì ta có \(3 - t = \sqrt {{t^2} - t - 6} \)\( \Leftrightarrow \left\{ \begin{array}{l}{t^2} - t - 6 = 9 - 6t + {t^2}\\t \le 3\end{array} \right.\)\( \Leftrightarrow t = 3\)\( \Leftrightarrow \sqrt {x + 7} = 3\)\( \Leftrightarrow x = 2\)
Nếu \(t < 1\) thì ta có \(1 + t = \sqrt {{t^2} - t - 6} \)\( \Leftrightarrow \left\{ \begin{array}{l}{t^2} - t - 6 = 1 + 2t + {t^2}\\t \ge - 1\end{array} \right.\)\( \Leftrightarrow t = - \dfrac{7}{3}\;\;\left( l \right)\).
Hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 1 \le 0\\x - m > 0\end{array} \right.$ có nghiệm khi
Ta có: $\left\{ \begin{array}{l}{x^2} - 1 \le 0\\x - m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 \le x \le 1\\x > m\end{array} \right.$.
Do đó hệ có nghiệm khi \(m < 1\).
Xác định $m$ để phương trình $\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0$ có ba nghiệm phân biệt lớn hơn $–1.$
Ta có $\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0$$ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} + 2\left( {m + 3} \right)x + 4m + 12 = 0\;\,\left( * \right)\end{array} \right.$.
Giả sử phương trình $\left( * \right)$ có hai nghiệm phân biệt ${x_1},{x_2}$, theo Vi-et ta có
$\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\left( {m + 3} \right)\\{x_1}.{x_2} = 4m + 12\end{array} \right.$.
Để phương trình $\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0$có ba nghiệm phân biệt lớn hơn $-1$. thì phương trình $\left( * \right)$ có hai nghiệm phân biệt ${x_1},{x_2}$ khác $1$ và đều lớn hơn $ - 1$.
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\1 + 2\left( {m + 3} \right) + 4m + 12 \ne 0\\{x_2} > {x_1} > - 1\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 3} \right)^2} - \left( {4m + 12} \right) > 0\\6m + 19 \ne 0\\\left( {{x_1} + 1} \right) + \left( {{x_2} + 1} \right) > 0\\\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2m - 3 > 0\\m \ne - \dfrac{{19}}{6}\\ - 2\left( {m + 3} \right) + 2 > 0\\4m + 12 - 2\left( {m + 3} \right) + 1 > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 1\\m < - 3\end{array} \right.\\m \ne - \dfrac{{19}}{6}\\m < - 2\\m > - \dfrac{7}{2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{7}{2} < m < - 3\\m \ne - \dfrac{{19}}{6}\end{array} \right.$.
