Trả lời bởi giáo viên
Đáp án đúng: a
Bất phương trình x3+3x2−6x−8≥0⇔(x−2)(x2+5x+4)≥0.
Phương trình x2+5x+4=0⇔[x=−4x=−1 và x−2=0⇔x=2.
Lập bảng xét dấu
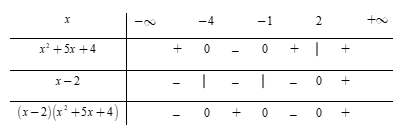
Dựa vào bảng xét dấu, ta thấy rằng (x−2)(x2+5x+4)≥0⇔x∈[−4;−1]∪[2;+∞).
Hướng dẫn giải:
Lập bảng xét dấu vế trái của bất phương trình và kết luận nghiệm.

