Để phương trình sau có 4 nghiệm phân biệt: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) thì giá trị của tham số \(a\) là:
Xét phương trình: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) (1)
\( \Leftrightarrow a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
Xét \(f\left( x \right) = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
\( = \left\{ \begin{array}{l}\left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 \ge 0\\ - \left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 < 0\end{array} \right.\)
\( = \left\{ \begin{array}{l} - 3{x^2} + 15x - 8 & {\rm{khi }}1 \le x \le 4\\{x^2} - 5x + 8 & {\rm{khi }}x \le 1 \vee x \ge 4\end{array} \right.\)
Bảng biến thiên:
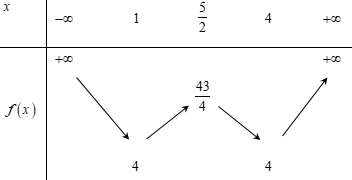
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt \( \Leftrightarrow 4 < a < \dfrac{{43}}{4}\).
Để bất phương trình \(\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\) nghiệm đúng \(\forall x \in \left[ { - 5;3} \right]\), tham số \(a\) phải thỏa điều kiện:
\(\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} \le {x^2} + 2x + a \Leftrightarrow \sqrt { - {x^2} - 2x + 15} - {x^2} - 2x \le a\)
Đặt \(t = \sqrt { - {x^2} - 2x + 15} \), ta có bảng biến thiên
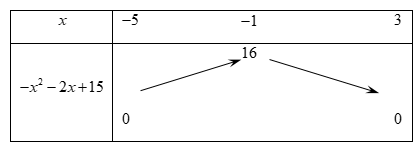
Suy ra \(t \in \left[ {0;4} \right]\).
Bất phương trình đã cho thành ${t^2} + t - 15 \le a$.
Xét hàm $f\left( t \right) = {t^2} + t - 15$ với \(t \in \left[ {0;4} \right]\)
Ta có bảng biến thiên
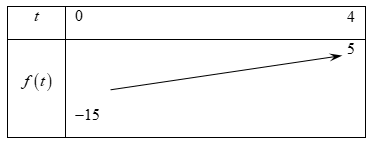
Bất phương trình \({t^2} + t - 15 \le a\) nghiệm đúng \(\forall t \in \left[ {0;4} \right]\) khi và chỉ khi \(a \ge 5.\)
Cho bất phương trình: ${x^2} - 2x \le \left| {x - 2} \right| + ax - 6$. Giá trị dương nhỏ nhất của $a$ để bất phương trình có nghiệm gần nhất với số nào sau đây:
Trường hợp 1: $x \in \left[ {2; + \infty } \right)$.
Khi đó bất phương trình đã cho trở thành:
${x^2} - \left( {a + 3} \right)x + 8 \le 0$$ \Leftrightarrow a \ge x + \dfrac{8}{x} - 3 \ge 4\sqrt 2 - 3 \approx 2,65$$\forall x \in \left[ {2; + \infty } \right)$.
Dấu xảy ra khi $x = 2\sqrt 2 $.
Trường hợp 2: $x \in \left( { - \infty ;2} \right)$.
Khi đó bất phương trình đã cho trở thành:
${x^2} - \left( {a + 1} \right)x + 4 \le 0$
$\Leftrightarrow ax \ge {x^2} -x+4$
$ \Leftrightarrow \left[ \begin{array}{l}a \ge \dfrac{{x^2} -x+4}{x}\;\;khi\;\;x \in \left( {0;2} \right)\;\;\;\;\;\;\\a \le \dfrac{{x^2} -x+4}{x}\;\;khi\;\;x \in \left( { - \infty ;0} \right)\;\;\;\end{array} \right.$.
$ \Leftrightarrow \left[ \begin{array}{l}a \ge x + \dfrac{4}{x} - 1\;\;khi\;\;x \in \left( {0;2} \right)\;\;\;\;\;\;\left( 1 \right)\\a \le x + \dfrac{4}{x} - 1\;\;khi\;\;x \in \left( { - \infty ;0} \right)\;\;\;\left( 2 \right)\end{array} \right.$.
Giải $\left( 1 \right)$ ta được $a > 3$ (theo bất đẳng thức Cauchy).
Giải $\left( 2 \right)$: $a \le x + \dfrac{4}{x} - 1$$ \Leftrightarrow a \le - 2\sqrt {x.\dfrac{4}{x}} - 1 = - 5$.
Vậy giá trị dương nhỏ nhất của $a$ gần với số $2,6$.
Bất phương trình: $\left| {{x^4} - 2{x^2} - 3} \right| \le {x^2} - 5$ có bao nhiêu nghiệm nghiệm nguyên?
Đặt \(t = {x^2} \ge 0\)
Ta có \(\left| {{t^2} - 2t - 3} \right| \le t - 5\).
Nếu \({t^2} - 2t - 3 \ge 0 \Leftrightarrow \left[ \begin{array}{l}t \le - 1\\t \ge 3\end{array} \right.\) thì ta có \({t^2} - 3t + 2 \le 0 \Leftrightarrow 1 \le t \le 2\) loại
Nếu \({t^2} - 2t - 3 < 0 \Leftrightarrow - 1 < t < 3\) thì ta có \( - {t^2} + t + 8 \le 0 \Leftrightarrow \left[ \begin{array}{l}t \le \dfrac{{1 - \sqrt {33} }}{2}\\t \ge \dfrac{{1 + \sqrt {33} }}{2}\end{array} \right.\) loại.
Để phương trình: $\left| {x + 3} \right|(x - 2) + m - 1 = 0$có đúng một nghiệm, các giá trị của tham số \(m\)là:
Ta có $\left| {x + 3} \right|\left( {x - 2} \right) + m - 1 = 0 \Leftrightarrow m = 1 - \left| {x + 3} \right|\left( {x - 2} \right)$
Xét hàm số $y = 1 - \left| {x + 3} \right|(x - 2)$
Ta có $y = \left\{ \begin{array}{l} - {x^2} - x + 7\,\,\;khi\,\,\;x \ge - 3\\{x^2} + x - 5\,\,\;\;\;khi\,\;\;x < - 3\end{array} \right.$
Bảng biến thiên của $y = 1 - \left| {x + 3} \right|(x - 2)$
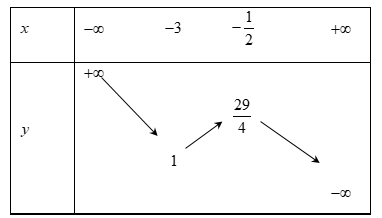
Dựa vào bảng trên phương trình có đúng $1$ nghiệm khi và chỉ khi$\left[ \begin{array}{l}m < 1\\m > \dfrac{{29}}{4}\end{array} \right.$
Bất phương trình \(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \) có nghiệm là
TXĐ: \(D = \mathbb{R}\)
\(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \)\( \Leftrightarrow {x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} < 0\)(1)
Đặt \(\sqrt {{x^2} + 5x + 28} = t\left( {t > 0} \right)\)
(1) trở thành: \({t^2} - 5t - 24 < 0 \Leftrightarrow - 3 < t < 8\)
\(\begin{array}{l} \Rightarrow {x^2} + 5x + 28 < 64\\ \Leftrightarrow {x^2} + 5x - 36 < 0 \Leftrightarrow - 9 < x < 4\end{array}\)
Tìm \(m\) để bất phương trình \(\sqrt {x - {m^2} - m} \left( {3 - \dfrac{{x + 1}}{{{x^3} - {x^2} - 3x + 3}}} \right) < 0\,\,(*)\) có nghiệm .
Ta có: \(\left( * \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{3 - \dfrac{{x + 1}}{{{x^3} - {x^2} - 3x + 3}} < 0}\\{x > {m^2} + m}\end{array}} \right.\)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\dfrac{{\left( {x - 2} \right)\left( {3{x^2} + 3x - 4} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - 3} \right)}} < 0}\\{x > {m^2} + m}\end{array}} \right.\) \(\left( {**} \right)\)
Bảng xét dấu:
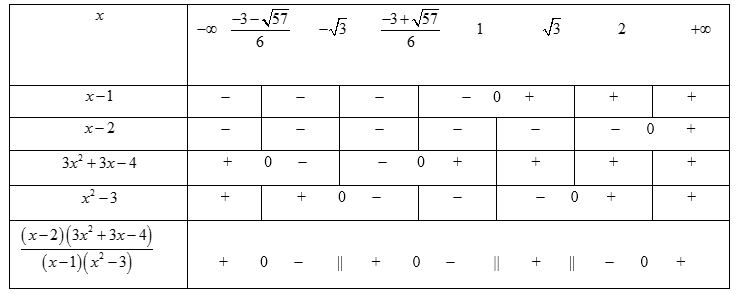
Tập nghiệm của bất phương trình \(\dfrac{{\left( {x - 2} \right)\left( {3{x^2} + 3x - 4} \right)}}{{\left( {x - 1} \right)\left( {{x^2} - 3} \right)}} < 0\) là \(S = \left( {\dfrac{{ - 3 - \sqrt {57} }}{6}; - \sqrt 3 } \right) \cup \left( {\dfrac{{ - 3 + \sqrt {57} }}{6};1} \right) \cup \left( {\sqrt 3 ;2} \right)\)
Do đó bất phương trình \(\left( * \right)\) có nghiệm khi và chỉ khi hệ bất phương trình\(\left( {**} \right)\) có nghiệm
\( \Leftrightarrow {m^2} + m < 2\)\( \Leftrightarrow {m^2} + m - 2 < 0\)\( \Leftrightarrow - 2 < m < 1\)
Vậy \( - 2 < m < 1\) là giá trị cần tìm.
Một viên gạch hình vuông có cạnh thay đổi được đặt nội tiếp trong một hình vuông có cạnh bằng 20cm, tạo thành bốn tam giác xung quanh như hình vẽ.
Tìm tập hợp các giá trị của x để diện tích viên gạch không vượt quá \(208c{m^2}\).
Ta có: \(\angle CAB + \angle BAD + \angle DAE = {180^o}\)
\( \Rightarrow \angle CAB + \angle EAD = {90^o}\)
Mà \(\angle CAB + \angle CBA = {90^o}\) (\(\Delta CAB\) vuông tại C)
\( \Rightarrow \angle CBA = \angle EAD\) kết hợp \(AB = AD\,\,\,\left( {gt} \right)\)
\(\begin{array}{l} \Rightarrow \Delta CAB = \Delta EDA\,\,\,\left( {ch - gn} \right)\\ \Rightarrow CB = EA = x \Rightarrow CA = CE - EA = 20 - x\,\,\,\,\left( {cm} \right)\end{array}\)
Diện tích viên gạch là \(S = A{B^2} = C{B^2} + C{A^2} = {x^2} + {\left( {20 - x} \right)^2}\)
Vì \(S \le 208 \Leftrightarrow {x^2} + {\left( {20 - x} \right)^2} \le 208 \Leftrightarrow 2{x^2} - 40x + 192 \le 0 \Leftrightarrow 8 \le x \le 12\)Tập nghiệm của bất phương trình \(\left( {\sqrt {2x + 4} - \sqrt {x + 1} } \right)\left( {\sqrt {2x + 1} + \sqrt {x + 4} } \right) \le x + 3\) là tập con của tập hợp nào sau đây?
ĐKXĐ: \(x \ge - \dfrac{1}{2}\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\left( {\sqrt {2x + 4} - \sqrt {x + 1} } \right)\left( {\sqrt {2x + 1} + \sqrt {x + 4} } \right) \le x + 3\\ \Leftrightarrow \left( {\sqrt {2x + 4} - \sqrt {x + 1} } \right)\left( {\sqrt {2x + 4} + \sqrt {x + 1} } \right)\left( {\sqrt {2x + 1} + \sqrt {x + 4} } \right) \le \left( {x + 3} \right)\left( {\sqrt {2x + 4} + \sqrt {x + 1} } \right)\\ \Leftrightarrow \left( {x + 3} \right)\left( {\sqrt {2x + 1} + \sqrt {x + 4} } \right) \le \left( {x + 3} \right)\left( {\sqrt {2x + 4} + \sqrt {x + 1} } \right)\\ \Leftrightarrow \left( {x + 3} \right)\left( {\sqrt {2x + 1} + \sqrt {x + 4} - \sqrt {2x + 4} - \sqrt {x + 1} } \right) \le 0\\ \Leftrightarrow \sqrt {2x + 1} + \sqrt {x + 4} - \sqrt {2x + 4} - \sqrt {x + 1} \le 0\,\,\,\,\,\left( {do\,\,\,x + 3 > 0\,\,\,\forall x \ge - \dfrac{1}{2}} \right)\\ \Leftrightarrow \sqrt {2x + 1} + \sqrt {x + 4} \le \sqrt {2x + 4} + \sqrt {x + 1} \\ \Leftrightarrow 3x + 5 + 2\sqrt {\left( {2x + 1} \right)\left( {x + 4} \right)} \le 3x + 5 + 2\sqrt {\left( {2x + 4} \right)\left( {x + 1} \right)} \\ \Leftrightarrow \left( {2x + 1} \right)\left( {x + 4} \right) \le \left( {2x + 4} \right)\left( {x + 1} \right)\\ \Leftrightarrow 2{x^2} + 9x + 4 \le 2{x^2} + 6x + 4\\ \Leftrightarrow 3x \le 0 \Leftrightarrow x \le 0\end{array}\)
Kết hợp ĐKXĐ \( \Rightarrow x \in \left[ { - \dfrac{1}{2};0} \right] \subset \left( { - \dfrac{2}{3};\dfrac{1}{2}} \right)\)
Một nhà máy sản xuất bóng đèn trang trí với chi phí sản xuất 12 USD mỗi bóng đèn. Nếu giá bán mỗi bóng đèn là 20 USD thì nhà máy dự tính bán được 2000 bóng mỗi tháng. Nếu cứ tăng giá bán mỗi bóng đèn lên 1 USD thì số bóng đèn bán được mỗi tháng giảm đi 100 bóng đèn. Để nhà máy có lợi nhuận lớn nhất, giá bán mỗi bóng đèn là
Bước 1: Gọi x là số tiền tăng thêm của một tháng và biểu diễn số tiền bán 1 tháng theo x.
Số tiền bán mỗi bóng đèn là: \(20 + x\,\)(USD)
Số tiền lãi của 1 bóng đèn là: \(x + 8\) (USD)
Sau khi tăng \(x\) USD 1 bóng đèn thì số bóng bán được trong 1 tháng: \(2000 - 100x\)
Bước 2: Biểu diễn lợi nhuận theo x. Áp dụng BĐT Cauchy để tìm max.
\(\begin{array}{l}L = \left( {8 + x} \right).\left( {2000 - 100x} \right)\\ \Rightarrow 100L = \left( {800 + 100x} \right)(2000 - 100x) \le {\left( {\dfrac{{800 + 2000}}{2}} \right)^2}\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow 800 + 100x = 2000 - 100x \Leftrightarrow x = 6\)
Vậy số tiền mỗi bóng là \(20 + 6 = 26\) USD
