Trả lời bởi giáo viên
Đáp án đúng: c
Ta có: (∗)⇔{3−x+1x3−x2−3x+3<0x>m2+m⇔{(x−2)(3x2+3x−4)(x−1)(x2−3)<0x>m2+m (∗∗)
Bảng xét dấu:
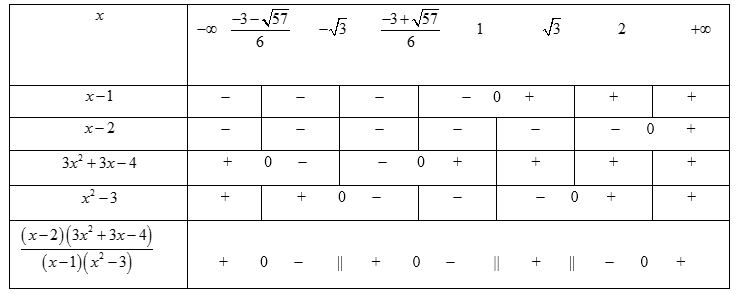
Tập nghiệm của bất phương trình (x−2)(3x2+3x−4)(x−1)(x2−3)<0 là S=(−3−√576;−√3)∪(−3+√576;1)∪(√3;2)
Do đó bất phương trình (∗) có nghiệm khi và chỉ khi hệ bất phương trình(∗∗) có nghiệm
⇔m2+m<2⇔m2+m−2<0⇔−2<m<1
Vậy −2<m<1 là giá trị cần tìm.
Hướng dẫn giải:
Đưa về dạng tìm m để hệ bất phương trình có nghiệm (giải bất phương trình và lập bảng xét dấu).

