Câu hỏi:
2 năm trước
Để bất phương trình √(x+5)(3−x)≤x2+2x+a nghiệm đúng ∀x∈[−5;3], tham số a phải thỏa điều kiện:
Trả lời bởi giáo viên
Đáp án đúng: c
√(x+5)(3−x)≤x2+2x+a⇔√−x2−2x+15−x2−2x≤a
Đặt t=√−x2−2x+15, ta có bảng biến thiên
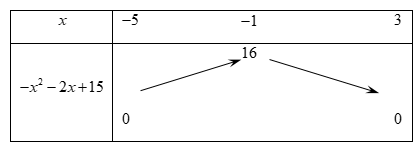
Suy ra t∈[0;4].
Bất phương trình đã cho thành t2+t−15≤a.
Xét hàm f(t)=t2+t−15 với t∈[0;4]
Ta có bảng biến thiên
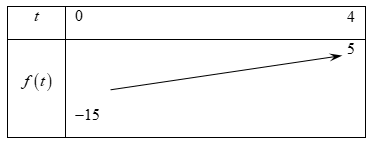
Bất phương trình t2+t−15≤a nghiệm đúng ∀t∈[0;4] khi và chỉ khi a≥5.
Hướng dẫn giải:
- Đặt t=√−x2−2x+15, tìm điều kiện của t với chú ý x∈[−5;3], biến đổi về dạng a≥f(t).
- Lập bảng biến thiên của hàm số f(t) trên đoạn D tìm được ở trên.
- Bất phương trình f(t)≤a nghiệm đúng ∀t∈D khi và chỉ khi a≥maxDf(t).

