Tuổi của 16 công nhân xưởng sản xuất được thống kê trong bảng sau.
|
Tuổi |
25 |
26 |
27 |
29 |
30 |
33 |
Cộng |
|
Số người |
2 |
3 |
4 |
3 |
3 |
1 |
16 |
Tìm số trung bình \(\overline x \) của mẫu số liệu trên.
Ta có: \(\overline x = \dfrac{{25.2 + 26.3 + 27.4 + 29.3 + 30.3 + 33.1}}{{16}} = 27,875.\)
Ta có bảng phân bố rời rạc:
|
x |
69 |
71 |
74 |
79 |
83 |
92 |
|
n |
1 |
1 |
1 |
1 |
2 |
1 |
\(\overline x = \dfrac{{69 + 71 + 74 + 79 + 83.2 + 92}}{7} = \dfrac{{551}}{7}\)
\(S_x^2 = \dfrac{1}{7}\)\(\left( {{{69}^2} + {{71}^2} + {{74}^2} + {{79}^2} + {{2.83}^2} + {{92}^2}} \right)\)\( - {\left( {\dfrac{{551}}{7}} \right)^2} = \dfrac{{2726}}{{49}}\)
\( \Rightarrow {S_x} \approx 7,46.\)
Điểm kiểm tra học kỳ I môn Toán của hai lớp 10 được giáo viên thống kê trong bảng sau:
|
Lớp điểm |
Tần số |
|
[4;5] |
7 |
|
[5;6] |
65 |
|
[6;7] |
24 |
|
[7;8] |
4 |
\(\overline x = \dfrac{1}{n}\left( {{n_1}.{C_1} + {n_2}{C_2} + ... + {n_k}{C_k}} \right)\)
\( = \dfrac{{\left( {7.4,5 + 65.5,5 + 24.6,5 + 4.7,5} \right)}}{{7 + 65 + 24 + 4}}\)\( = 5,75\)
Phương sai của một mẫu số liệu \(\left\{ {{x_1};{x_2};...;{x_N}} \right\}\) bằng
Ta có: \(s = \sqrt {{s^2}} \) với \(s\) là độ lệch chuẩn và \({s^2}\) là phương sai của số liệu thống kê.
Cho mẫu số liệu \(\left\{ {{x_1};{x_2};...;{x_N}} \right\}\) có số trung bình \(\overline x \), mốt \({M_0}.\) Chọn khẳng định sai trong các khẳng định sau.
Ta có công thức: \({s^2} = \overline {{x^2}} - {\left( {\overline x } \right)^2}\)
Với \(\overline x \) là số trung bình cộng của số liệu thống kê và \(\overline {{x^2}} \) là trung bình cộng của các bình phương số liệu thống kê, tức là:
\(s = \sqrt {{s^2}} \) với \(s\) là độ lệch chuẩn và \({s^2}\) là phương sai của số liệu thống kê.
Mốt của một bảng phân bố tần số là giá trị có tần số lớn nhất và được kí hiệu là \({M_O}.\)
Mốt \({M_0}\) có thể nhỏ hơn số trung bình \(\overline x \).
Công thức tính giá trị trung bình đối với bảng phân bố tần số rời rạc là:
Công thức tính giá trị trung bình: \(\overline x = \dfrac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}}}{n}\)
Công thức tính phương sai nếu cho bảng phân bố tần số rời rạc là:
Công thức tính phương sai: \(s_X^2 = \dfrac{1}{n}\left[ {{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{x_k} - \overline x } \right)}^2}} \right]\)
Sản lượng lúa (đơn vị là tạ) của $40$ thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Phương sai là:
Ta có:
- Giá trị trung bình:
\(\overline x = \dfrac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}}}{n}\)\( = \dfrac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1\)
- Phương sai:
\(s_X^2 = \dfrac{1}{n}\left[ {{n_1}{{({x_1} - \overline x )}^2} + ... + {n_k}{{({x_k} - \overline x )}^2}} \right]\)
\( = \dfrac{1}{{40}}\left[ {5{{\left( {20 - 22,1} \right)}^2} + 8{{\left( {21 - 22,1} \right)}^2}} \right.\) \(\left. { + 11{{\left( {22 - 22,1} \right)}^2} + 10{{\left( {23 - 22,1} \right)}^2} + 6{{\left( {24 - 22,1} \right)}^2}} \right]\) \( = 1,54\)
Công thức tính độ lệch chuẩn nếu biết phương sai \(s_X^2\) là:
Ta có: \({s_X} = \sqrt {s_X^2} \) là độ lệch chuẩn.
Chọn phát biểu đúng:
Ta thấy độ lệch chuẩn \({s_X} = \sqrt {s_X^2} \) chính là căn bậc hai của phương sai.
Vậy phương sai bằng bình phương độ lệch chuẩn.
Sản lượng lúa (đơn vị là tạ) của $40$ thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Độ lệch chuẩn là:
- Giá trị trung bình:
\(\overline x = \dfrac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}}}{n}\)\( = \dfrac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1\)
- Phương sai:
\(s_X^2 = \dfrac{1}{n}\left[ {{n_1}{{({x_1} - \overline x )}^2} + ... + {n_k}{{({x_k} - \overline x )}^2}} \right]\)
\( = \dfrac{1}{{40}}\left[ {5{{\left( {20 - 22,1} \right)}^2} + 8{{\left( {21 - 22,1} \right)}^2}} \right.\) \(\left. { + 11{{\left( {22 - 22,1} \right)}^2} + 10{{\left( {23 - 22,1} \right)}^2} + 6{{\left( {24 - 22,1} \right)}^2}} \right]\) \( = 1,54\)
- Độ lệch chuẩn: \({s_X} = \sqrt {s_X^2} = \sqrt {1,54} \approx 1,24\)
Công thức nào sau đây đúng về độ lệch chuẩn biết giá trị trung bình \(\overline x \)?
Phương sai \(s_X^2 = \dfrac{1}{n}\left[ {{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{x_k} - \overline x } \right)}^2}} \right]\)
Do đó độ lệch chuẩn \({s_X} = \sqrt {\dfrac{1}{n}\left[ {{n_1}{{\left( {{x_1} - \overline x } \right)}^2} + {n_2}{{\left( {{x_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{x_k} - \overline x } \right)}^2}} \right]} \)
Mốt của mẫu số liệu là:
Mốt của mẫu số liệu là giá trị có tần số lớn nhất.
$41 $ học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm $30.$ Kết quả như sau:

Mốt của mẫu số liệu trên là:
Quan sát bảng mẫu số liệu ta thấy giá trị có tần số lớn nhất là \(18\) có tần số \(7\)
Sản lượng lúa (đơn vị là tạ) của $40$ thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Sản lượng trình bình của \(40\) thửa ruộng là:
Ta có: \(\overline x = \dfrac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}}}{n}\)\( = \dfrac{{20.5 + 21.8 + 22.11 + 23.10 + 24.6}}{{40}} = 22,1\)
Cho bảng số liệu điểm bài kiểm tra môn toán của 20 học sinh.
|
Điểm |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Cộng |
|
Số học sinh |
1 |
2 |
3 |
4 |
5 |
4 |
1 |
20 |
Tính số trung vị của bảng số liệu trên.
Do \(n = 20\)(số chẵn) nên \({M_e} = \dfrac{{{x_{10}} + {x_{11}}}}{2} = \dfrac{{7 + 8}}{2} = 7,5.\)
Cho mẫu số liệu thống kê \(\left\{ {1;2;3;4;5;6;7;8;9} \right\}.\) Tính (gần đúng) độ lệch chuẩn của mẫu số liệu trên?
\(\overline x = \dfrac{{1 + 2 + ... + 9}}{9} = 5.\)
Phương sai \(S_x^2 = \dfrac{1}{n}{\sum\limits_{i = 1}^k {{n_i}\left( {{x_i} - \overline x } \right)} ^2} \)\(= \dfrac{{{{\left( {1 - 5} \right)}^2} + {{\left( {2 - 5} \right)}^2} + ... + {{\left( {9 - 5} \right)}^2}}}{9} = \dfrac{{20}}{3}.\)
Độ lệch chuẩn \({S_x} = \sqrt {S_x^2} = \sqrt {\dfrac{{20}}{3}} \approx 2,58.\)
Có 100 học sinh tham dự kì thi học sinh giỏi Toán cấp tỉnh (thang điểm 20). Kết quả như sau:
|
Điểm |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
Tần số |
1 |
1 |
3 |
5 |
8 |
13 |
19 |
24 |
14 |
10 |
2 |
Huyết áp tối thiểu tính bằng mmHg của 2750 người lớn (nữ) như sau.
|
Huyết áp |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
|
Người |
8 |
8 |
90 |
186 |
394 |
464 |
598 |
431 |
315 |
185 |
46 |
25 |
Số trung bình cộng và phương sai của bảng trên là.
Tại Hà Nội, giá nước sinh hoạt được tính như bảng sau (Đơn vị tính: đồng/\({m^3}\))
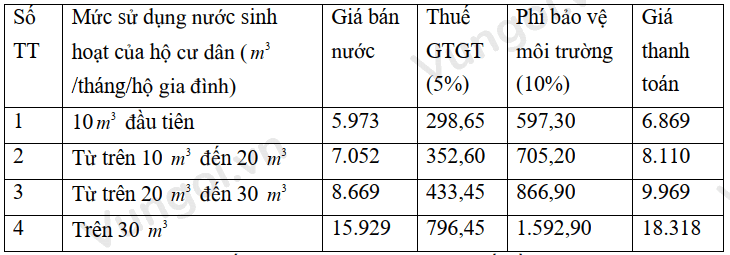
Một hộ gia đình tiêu thụ hết 40 \({m^3}\) nước một tháng thì số tiền phải trả là
Số tiền phải trả khi tiêu thụ hết 40 m3 nước một tháng là:
\(10.6,869 + 10.8,110 + 10.9,969 + 10.18,318 = 432\,660\)(đồng)

