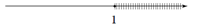Cho hai tập hợp \(A = \left[ { - 2;7} \right),{\rm{ }}B = \left( {1;9} \right]\). Kết quả của phép toán \(A \cup B\) là
Ta có: \(A = \left[ { - 2;7} \right),B = \left( {1;9} \right]\)

\( \Rightarrow A \cup B = \left[ { - 2;9} \right]\)
Cho \(A = \left\{ {x \in R:\left| x \right| \le 5} \right\}.\)Phần bù của \(A\) trong tập số thực là:
\(\begin{array}{l}A = \left\{ {x \in R:\left| x \right| \le 5} \right\}\\ = \left\{ {x \in R: - 5 \le x \le 5} \right\} \\= \left[ { - 5;5} \right]\end{array}\)
Xét trục số:

$\mathbb{R}\backslash A = \left( { - \infty ; - 5} \right) \cup \left( {5; + \infty } \right)$
Cho các tập hợp: \(A = \left( { - \infty ;3} \right),\)\(B = \left\{ {x \in R\left| {x \ge 5} \right.} \right\},\)\(C = \left[ {1;7} \right)\). Tập hợp \(A \cap \left( {B \cup C} \right)\) là:
\(\begin{array}{l}B = \left\{ {x \in R\left| {x \ge 5} \right.} \right\} = \left[ {5; + \infty } \right)\\A = \left( { - \infty ;3} \right),B = \left[ {5; + \infty } \right),C = \left[ {1;7} \right)\end{array}\)
Xét trục số:
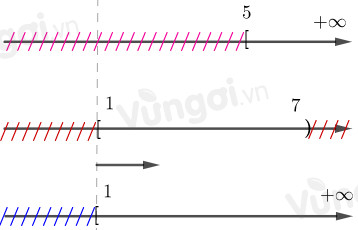
$=>B \cup C = \left[ {1; + \infty } \right)$
Xét trục số:
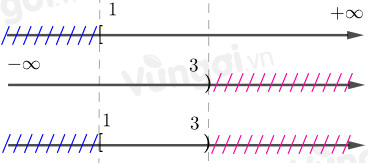
$A \cap \left( {B \cup C} \right) = \left[ {1;3} \right)$
Cho tập hợp \(A = \left( {2; + \infty } \right)\) . Khi đó tập \({C_\mathbb{R}}A\) là
\(A = \left( {2; + \infty } \right) \Rightarrow {C_\mathbb{R}}A = \mathbb{R}\backslash A = \left( { - \infty ;2} \right]\)
Cho tập hợp \(A = \left[ { - 2;3} \right],B = \left( {1;5} \right]\). Khi đó tập \(A\backslash B\) là
\(A = \left[ { - 2;3} \right],B = \left( {1;5} \right]\)
Xét trục số:
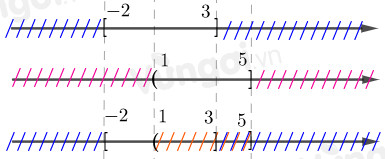
\( \Rightarrow A\backslash B = \left[ { - 2;1} \right]\)
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp \(A = \left\{ {\left. {x \in \mathbb{R}} \right|4 \le x \le 9} \right\}\):
\(A = \left\{ {\left. {x \in \mathbb{R}} \right|4 \le x \le 9} \right\}\)\( \Leftrightarrow A = \left[ {4;9} \right].\)
Cho \(A = \left[ {1;4} \right];B = \left( {2;6} \right);C = \left( {1;2} \right).\) Tìm \(A \cap B \cap C:\)
\(A = \left[ {1;4} \right];B = \left( {2;6} \right);C = \left( {1;2} \right)\)
Xét trục số: $ A \cap B $
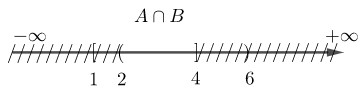
\( \Rightarrow A \cap B = \left( {2;4} \right]\)

Xét trục số: $ A \cap B \cap C$
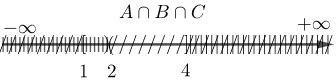
\( \Rightarrow A \cap B \cap C = \emptyset \).
Cho hai tập \(A = \left\{ {\left. {x \in \mathbb{R}} \right|x + 3 < 4 + 2x} \right\}\), \(B = \left\{ {\left. {x \in \mathbb{R}} \right|5x - 3 < 4x - 1} \right\}\).
Tất cả các số tự nhiên thuộc cả hai tập \(A\) và \(B\) là:
\(A = \left\{ {\left. {x \in \mathbb{R}} \right|x + 3 < 4 + 2x} \right\}\)$= \left\{ {\left. {x \in \mathbb{R}} \right|x>-1} \right\}$
\( \Rightarrow A = \left( { - 1;\, + \infty } \right).\)
\(B = \left\{ {\left. {x \in \mathbb{R}} \right|5x - 3 < 4x - 1} \right\} \)$ = \left\{ {\left. {x \in \mathbb{R}} \right|x <2} \right\} $
\( \Rightarrow B = \left( { - \infty ;\,2} \right).\)
Xét trục số: Tập A ta bỏ phần bên trái $-1$, tập B thì bỏ phần bên phải 2

\(A \cap B = \left( { - 1;\,2} \right)\)\( \Leftrightarrow A \cap B = \left\{ {\left. {x \in \mathbb{R}} \right| - 1 < x < 2} \right\}.\)
\( \Rightarrow A \cap B = \left\{ {\left. {x \in \mathbb{N}} \right| - 1 < x < 2} \right\}\)\( \Leftrightarrow A \cap B = \left\{ {0;1} \right\}.\)
Cho \(A = \left\{ {x \in R:x + 2 \ge 0} \right\},B = \left\{ {x \in R:6 - x \ge 0} \right\}\). Khi đó \(A\backslash B\) là:
Ta có \(A = \left\{ {x \in R:x + 2 \ge 0} \right\}\)\( \Rightarrow A = \left[ { - 2;\, + \infty } \right)\), \(B = \left\{ {x \in R:6 - x \ge 0} \right\}\)\( \Rightarrow B = \left( { - \infty ;\,6} \right]\).
Vậy \(A\backslash B = \left( {6;\, + \infty } \right).\)
Cho tập hợp \(A = \left( { - \infty ;5} \right]\), \(B = \left\{ {x \in \mathbb{R}| - 1 < x \le 6} \right\}\). Khi đó \(A\backslash B\) là:
Ta có: \(B = \left\{ {x \in R| - 1 < x \le 6} \right\} = \left( { - 1;6} \right]\)
Do đó \(A\backslash B = \left( { - \infty ;5} \right]\backslash \left( { - 1;6} \right] = \left( { - \infty ; - 1} \right]\)

Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập \(A = \left\{ {x \in \mathbb{R}\left| {\left| x \right| \ge 1} \right.} \right\}\)?
Ta có \(\left| x \right| \ge 1 \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x \le - 1\end{array} \right.\) nên hình minh họa cho tập \(A\) đáp án A.
Cho \(A = \left[ { - 4;7} \right]\), \(B = \left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right)\). Khi đó \(A \cap B\):
\(A = \left[ { - 4;7} \right]\), \(B = \left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right)\), suy ra \(A \cap B = \left[ { - 4;\, - 2} \right) \cup \left( {3;\,7} \right]\).
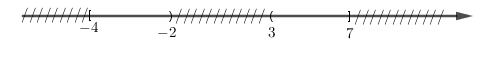
Cho \(A = \left\{ {x \in R:x + 2 \ge 0} \right\}\), \(B = \left\{ {x \in R:5 - x \ge 0} \right\}\). Khi đó \(A \cap B\) là
Ta có \(A = \left\{ {x \in R:x + 2 \ge 0} \right\}\)\( \Rightarrow A = \left[ { - 2;\, + \infty } \right)\), \(B = \left\{ {x \in R:5 - x \ge 0} \right\}\)\( \Rightarrow B = \left( { - \infty ;\,5} \right]\)
Vậy \(A \cap B = \left[ { - 2;\,5} \right].\)
Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp \(A = \left[ { - 4;4} \right] \cup \left[ {7;9} \right] \cup \left[ {1;9} \right]\).
Xét trục số: $ \left[ { - 4;4} \right] \cup \left[ {7;9} \right] $

Xét trục số: $ \left[ { - 4;4} \right] \cup \left[ {7;9} \right] \cup \left[ {1;9} \right] $
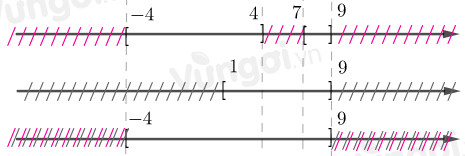
Vậy \(A = \left[ { - 4;4} \right] \cup \left[ {7;9} \right] \cup \left[ {1;9} \right] = \left[ { - 4;9} \right]\).
Cho \(A = \left[ {0;3} \right],{\rm{ }}B = \left( {1;5} \right)\) và \(C = \left( {0;1} \right).\) Khẳng định nào sau đây sai?
Xét các đáp án:
Đáp án A. Ta có \(A \cap B = \left[ {0;3} \right] \cap \left( {1;5} \right) = \left( {1;3} \right]\)\( \Rightarrow A \cap B \cap C = \left( {1;3} \right] \cap \left( {0;1} \right) = \emptyset \)
Đáp án B. Ta có \(A \cup B = \left[ {0;3} \right] \cup \left( {1;5} \right) = \left[ {0;5} \right)\)\( \Rightarrow A \cup B \cup C = \left[ {0;5} \right) \cup \left( {0;1} \right) = \left[ {0;5} \right)\)
Đáp án C. Ta có \(A \cup C = \left[ {0;3} \right] \cup \left( {0;1} \right) = \left[ {0;3} \right]\)\( \Rightarrow \left( {A \cup C} \right)\backslash C = \left[ {0;3} \right]\backslash \left( {0;1} \right) = \left\{ 0 \right\} \cup \left[ {1;3} \right]\)
Đáp án D. Ta có \(A \cap B = \left( {1;3} \right]\)\( \Rightarrow \left( {A \cap B} \right)\backslash C = \left( {1;3} \right]\backslash \left( {0;1} \right) = \left( {1;3} \right]\)
Cho tập \(X = \left[ { - 3;2} \right)\). Phần bù của \(X\) trong \(\mathbb{R}\) là tập nào trong các tập sau?
Ta có \({{\rm{C}}_\mathbb{R}}A = \mathbb{R}\backslash A = \left( { - \infty ; - 3} \right) \cup \left[ {2; + \infty } \right)\).
Cho tập \(A = \left\{ {x \in \mathbb{R}\left| {\left| x \right| \ge 5} \right.} \right\}.\) Khẳng định nào sau đây đúng?
Ta có \(A = \left\{ { x \in \mathbb{R}\left| {\left| x \right| \ge 5} \right.} \right\} = \left( { - \infty ; - 5} \right] \cup \left[ {5; + \infty } \right)\) \( \Rightarrow {C_\mathbb{R}}A = \left( { - 5;5} \right)\)
Cho \({C_\mathbb{R}}A = \left( { - \infty ;3} \right) \cup \left[ {5; + \infty } \right)\) và \({C_\mathbb{R}}B = \left[ {4;7} \right)\). Xác định tập \(X = A \cap B.\)
Ta có:
\( \bullet \) \({C_\mathbb{R}}A = \left( { - \infty ;3} \right) \cup \left[ {5; + \infty } \right) \Rightarrow A\left[ {3;5} \right).\)
\( \bullet \) \({C_\mathbb{R}}B = \left[ {4;7} \right) \Rightarrow B = \left( { - \infty ;4} \right) \cup \left[ {7; + \infty } \right).\)
Suy ra \(X = A \cap B = \left[ {3;4} \right).\)
Cho hai tập hợp \(A = \left[ { - 2;3} \right]\) và \(B = \left( {1; + \infty } \right).\) Xác định \({C_\mathbb{R}}\left( {A \cup B} \right).\)
Ta có \(A \cup B = \left[ { - 2; + \infty } \right)\) \( \Rightarrow {C_\mathbb{R}}\left( {A \cup B} \right) = \left( { - \infty ; - 2} \right)\)
Cho hai tập hợp \(A = \left( {m - 1;5} \right)\,\) và \(B = \left( {3; + \infty } \right)\). Tìm tất cả các giá trị thực của tham số \(m\) để \(A\backslash B = \emptyset \).
Điều kiện: \(m - 1 < 5 \Leftrightarrow m < 6\).
Để \(A\backslash B = \emptyset \) khi và chỉ khi \(A \subset B\), tức là \(3 \le m - 1 \Leftrightarrow m \ge 4\).
Đối chiếu điều kiện, ta được \(4 \le m < 6\).