Các tập hợp số

Điều kiện: \(\left\{ \begin{array}{l}m - 1 < 4\\ - 2 < 2m + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m >  - 2\end{array} \right.\)\( \Leftrightarrow  - 2 < m < 5\)

\(A \cap B \ne \emptyset  \Leftrightarrow \left\{ \begin{array}{l} - 2 < 4\\m - 1 < 2m + 2\end{array} \right. \)\(\Leftrightarrow  - m < 3 \Leftrightarrow m >  - 3\).

Kết hợp với điều kiện ta có: \( - 2 < m < 5\)

Ta có \({C_\mathbb{R}}B = \left( { - \infty ;3m - 1} \right) \cup \left( {3m + 3; + \infty } \right)\).

Do đó, để \(A \subset {C_\mathbb{R}}B \Leftrightarrow m \le 3m - 1 \Leftrightarrow m \ge \dfrac{1}{2}\).

Để \(A \cup B = \mathbb{R}\) thì \(m \ge 2\).

Để \(A \cap B = \emptyset \) thì \(\left[ \begin{array}{l}m + 1 < 0\\m \ge 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m <  - 1\\m \ge 3\end{array} \right.\) hay \(m \in \left( { - \infty ; - 1} \right) \cup \left[ {3; + \infty } \right)\).

Ta có:   \(\left\{ \begin{array}{l}A = \left\{ {x \in \mathbb{R}|\,x < 3} \right\} = \left( { - \infty ;\,3} \right)\\B = \left\{ {x \in \mathbb{R}|\,\,1 < x \le 5} \right\} = \left( {1;\,\,5} \right]\\C = \left\{ {x \in \mathbb{R}| - 2 \le x \le 4} \right\} = \left[ { - 2;\,\,4} \right]\end{array} \right..\)

Xét trục số: $A \cap C$

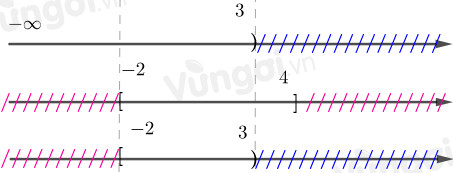
Tương tự với $B \cup C$

Bằng cách biểu diễn trên trục số ta có: \(\left\{ \begin{array}{l}A \cap C = \left[ { - 2;3} \right)\\B \cup C = \left[ { - 2;5} \right]\end{array} \right..\)

\( \Rightarrow \left( {B \cup C} \right)\backslash \left( {A \cap C} \right) = \left[ {3;5} \right].\)

Điều kiện: \(m \in \mathbb{R}\).

Để \(B \subset A\) khi và chỉ khi \(\left\{ \begin{array}{l}m - 7 \ge  - 4\\m \le 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge 3\\m \le 3\end{array} \right. \Leftrightarrow m = 3\).

Ta tìm \(m\) để \(A \cap B = \emptyset .\) Ta có 2 trường hợp sau:

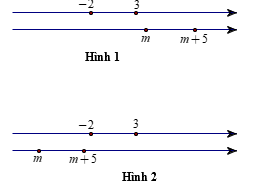
Trường hợp 1. (Xem hình vẽ 1) Để \(A \cap B = \emptyset  \Leftrightarrow m \ge 3.\)

Trường hợp 2. (Xem hình vẽ 2) Để \(A \cap B = \emptyset  \Leftrightarrow m + 5 \le  - 2 \Leftrightarrow m \le  - 7.\)

Kết hợp hai trường hợp ta được \(\left[ \begin{array}{l}m \ge 3\\m \le  - 7\end{array} \right.\) thì \(A \cap B = \emptyset .\)

Suy ra để \(A \cap B \ne \emptyset \) thì \( - 7 < m < 3.\)

Điều kiện: \(m \ge  - 3\).

Để \(A \cup B = A\) khi và chỉ khi \(B \subset A\), tức là \(m \le 1\).

Đối chiếu điều kiện, ta được \( - 3 \le m \le 1\).

Ta có $ \left( {1;{\rm{ }}m} \right] \cap \left( {2;{\rm{ }} + \infty } \right) \ne \emptyset $ khi m nằm bên phải 2:

\( \Rightarrow \left( {1;{\rm{ }}m} \right] \cap \left( {2;{\rm{ }} + \infty } \right) \ne \emptyset  \Leftrightarrow m > 2.\)

Vẽ trục số: 

- Vẽ khoảng $[-4;3]$

- Gạch bỏ phần ngoài của $[-4;3]$ 

- Rồi vẽ $[-2;1]$, gạch phần này đi.

- Phần khoảng trắng còn lại là kết quả cần tìm.

Bằng cách vẽ trục số như trên, ta có: \(\,\left[ { - 4;3} \right]\backslash \left[ { - 2;1} \right] = \left[ { - 4; - 2} \right) \cup \left( {1;3} \right]\)

TH1: \(m+2<n\)

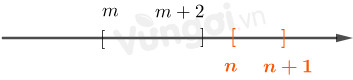
TH2: \(m > n + 1\)

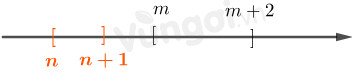
Từ hai trường hợp trên ta có:

\(A \cap B = \emptyset  \Leftrightarrow \left[ \begin{array}{l}m + 2 < n\\m > n + 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m - n <  - 2\\m - n > 1\end{array} \right.\)

Điều kiện để tồn tại tập hợp \(A\) là:  \(m - 1 \le \dfrac{{m + 1}}{2} \Leftrightarrow 2m - 2 < m + 1 \)\(\Leftrightarrow m \le 3\,\,\,\,\left( * \right)\)

\(A \subset B \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{A \subset \left( { - \infty ; - 2} \right)}\\{A \subset \left[ {2; + \infty } \right)}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\dfrac{{m + 1}}{2} <  - 2}\\{m - 1 \ge 2}\end{array}} \right. \\\Leftrightarrow \left[ \begin{array}{l}m + 1 <  - 4\\m \ge 3\end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m <  - 5}\\{m \ge 3}\end{array}} \right.\)

Kết hợp với điều kiện (*) ta có \(\left[ \begin{array}{l}m <  - 5\\m = 3\end{array} \right.\) là các giá trị cần tìm.

Điều kiện để tồn tại tập hợp \(A\) là: \(m - 1 \le \dfrac{{m + 1}}{2} \Leftrightarrow 2m - 2 \le m + 1\)\( \Leftrightarrow m \le 3\,\,\,\,\left( * \right)\)

Biểu diễn trên trục số:

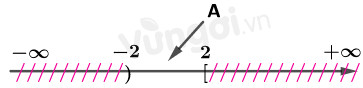
\( \Rightarrow A \cap B = \emptyset  \Leftrightarrow A \subset \left[ { - 2;\,\,2} \right)\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{ - 2 \le m - 1}\\{\dfrac{{m + 1}}{2} < 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ge  - 1}\\{m < 3}\end{array}} \right.\\ \Leftrightarrow  - 1 \le m < 3\)

Kết hợp với điều kiện (*) ta có \( - 1 \le m < 3\) là các giá trị cần tìm.

\(A = \left( {A \cap B} \right) \cup \left( {A\backslash B} \right) = \left[ {1;4} \right] \cup \left( { - 3;1} \right) = \left( { - 3;4} \right]\)

\(B = \left( {A \cup B} \right)\backslash \left( {A\backslash B} \right) = \left( { - 3;8} \right)\backslash \left( { - 3;1} \right) = \left[ {1;8} \right)\)

\(x \in A \cap B \Leftrightarrow \left\{ \begin{array}{l}x \in A\\x \in B\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x < 0\\x \in \mathbb{Q}\\ - 6 \le x < 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \in \mathbb{Q}\\ - 6 \le x < 0\end{array} \right.\)

Suy ra, \(A \cap B = \left\{ {x \in \mathbb{Q}\left| { - 6 \le x < 0} \right.} \right\}\)

Ta có \(\left( { - \infty ;m} \right) \cap \left[ { - 3;5} \right) \ne \emptyset  \Leftrightarrow m >  - 3\)

Biểu biễn trên trục số:

Với \(m =  - 3\) thì \(\left( { - \infty ; - 3} \right) \cap \left[ { - 3;5} \right) = \emptyset \) nên loại A,B,C.

Với \(A = \left( {m-1;\,\,4} \right],{\rm{ }}B = \left( {-2;\,\,2m + 2} \right)\) khác tập rỗng.

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}m - 1 < 4\\2m + 2 >  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 5\\m >  - 2\end{array} \right.\\ \Leftrightarrow  - 2 < m < 5\,\,\,\,\,\left( * \right).\\ \Rightarrow A \cap B = \left[ \begin{array}{l}\left( {m - 1;\,\,2m + 2} \right)\\\left( { - 2;\,\,2m + 2} \right)\\\left( {m - 1;\,\,4} \right]\\\left( { - 2;\,\,4} \right]\end{array} \right. \\\left( {A \cap B} \right) \subset \left( { - 1\,;\,\,3} \right)\\ \Leftrightarrow \left( {m - 1;\,\,2m + 2} \right) \subset \left( { - 1\,;\,\,3} \right) \\ \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ge  - 1\\2m + 2 \le 3\end{array} \right. \Leftrightarrow 0 \le m \le \dfrac{1}{2}\,\,\,\,\left( {tm\,\,\,\left( * \right)} \right)\end{array}\)

Ta có: \({C_\mathbb{R}}A = \left[ {m; + \infty } \right)\)

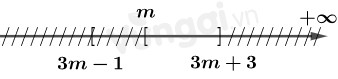
\( \Rightarrow {C_\mathbb{R}}A \cap B \ne \emptyset  \)\(\Leftrightarrow m \le 3m + 3 \Leftrightarrow m \ge  - \dfrac{3}{2}.\)

Vậy \(m \ge  - \dfrac{3}{2}\) là giá trị cần tìm.

Ta có : \(A \cup B = \left\{ {x \in \mathbb{R}:\,\,x \in A\,\,\,hoac\,\,x \in B} \right\}.\)

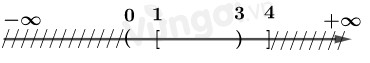
\( \Rightarrow \left( {0;3} \right) \cup \left[ {1;4} \right] = \left( {0;4} \right]\)

Ta có: \(A = \{ x \in R\left| {1 < x \le 2\} } \right. = \left( {1;2} \right]\)