Câu hỏi:

2 năm trước

Cho các tập hợp: $A = \left\{ {x \in \mathbb{R}|\,x < 3} \right\}{\rm{, }}$ $B = \left\{ {x \in \mathbb{R}|\,1 < x \le 5} \right\}{\rm{,}}$ $C = \left\{ {x \in \mathbb{R}|\, - 2 \le x \le 4} \right\}.$

Tìm $\left( {B \cup C} \right)\backslash \left( {A \cap C} \right)$

$\left[ {3;5} \right]$

$\left[ {3;4} \right]$

$\left( {3;5} \right)$

$\left[ {1;5} \right]$

Xem đáp án

56 lượt xem

Các tập hợp số - MÔN TOÁN - Lớp 10. Thi ngay

Trả lời bởi giáo viên

Đáp án đúng: a

Ta có: $\left\{ \begin{array}{l}A = \left\{ {x \in \mathbb{R}|\,x < 3} \right\} = \left( { - \infty ;\,3} \right)\\B = \left\{ {x \in \mathbb{R}|\,\,1 < x \le 5} \right\} = \left( {1;\,\,5} \right]\\C = \left\{ {x \in \mathbb{R}| - 2 \le x \le 4} \right\} = \left[ { - 2;\,\,4} \right]\end{array} \right..$

Xét trục số: $A \cap C$

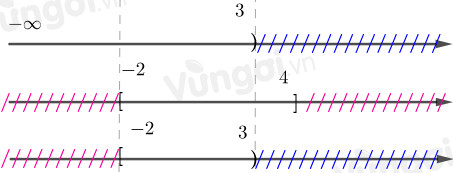
Tương tự với $B \cup C$

Bằng cách biểu diễn trên trục số ta có: $\left\{ \begin{array}{l}A \cap C = \left[ { - 2;3} \right)\\B \cup C = \left[ { - 2;5} \right]\end{array} \right..$

$\Rightarrow \left( {B \cup C} \right)\backslash \left( {A \cap C} \right) = \left[ {3;5} \right].$

Hướng dẫn giải:

Tìm A, B, C từ đó tìm $A \cap C$ và $B \cup C$ để tìm $\left( {B \cup C} \right)\backslash \left( {A \cap C} \right)$

Câu hỏi khác

Câu 1:

Cho hai tập hợp $A = \left[ { - 2;7} \right),{\rm{ }}B = \left( {1;9} \right]$ . Kết quả của phép toán $A \cup B$ là

$\left[ { - 2;1} \right)$

$\left( {7;9} \right]$

$\left[ { - 2;9} \right]$

Xem đáp án

93 lượt xem
Xem đáp án
2 năm trước

Câu 2:

Cho $A = \left\{ {x \in R:\left| x \right| \le 5} \right\}.$ Phần bù của $A$ trong tập số thực là:

$\left[ { - 5;5} \right].$

$\left( { - \infty ; - 5} \right] \cup \left[ {5; + \infty } \right).$

$\left( { - \infty ; - 5} \right) \cup \left( {5; + \infty } \right).$

$\left( { - 5;5} \right).$

Xem đáp án

106

106 lượt xem
Xem đáp án
2 năm trước

Câu 3:

Cho các tập hợp: $A = \left( { - \infty ;3} \right),$ $B = \left\{ {x \in R\left| {x \ge 5} \right.} \right\},$ $C = \left[ {1;7} \right)$ . Tập hợp $A \cap \left( {B \cup C} \right)$ là:

$\left[ {5;7} \right)$

$\left[ {1;3} \right)$

$\emptyset$

$\left[ {1;5} \right]$

Xem đáp án

103

103 lượt xem
Xem đáp án
2 năm trước

Câu 4:

Cho tập hợp $A = \left( {2; + \infty } \right)$ . Khi đó tập ${C_\mathbb{R}}A$ là

$\left[ {2; + \infty } \right)$

$\left( {2; + \infty } \right)$

$\left( { - \infty ;2} \right]$

$\left( { - \infty ; - 2} \right]$

Xem đáp án

118

118 lượt xem
Xem đáp án
2 năm trước

Câu 5:

Cho tập hợp $A = \left[ { - 2;3} \right],B = \left( {1;5} \right]$ . Khi đó tập $A\backslash B$ là

$\left( { - 2;1} \right]$

$\left( { - 2; - 1} \right)$

$\left[ { - 2;1} \right)$

$\left[ { - 2;1} \right]$

Xem đáp án

98 lượt xem
Xem đáp án
2 năm trước

Câu 6:

Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp $A = \left\{ {\left. {x \in \mathbb{R}} \right|4 \le x \le 9} \right\}$ :

$A = \left[ {4;9} \right].$

$A = \left( {4;9} \right].$

$A = \left[ {4;9} \right).$

$A = \left( {4;9} \right).$

Xem đáp án

100

100 lượt xem
Xem đáp án
2 năm trước

Câu 7:

Cho $A = \left[ {1;4} \right];B = \left( {2;6} \right);C = \left( {1;2} \right).$ Tìm $A \cap B \cap C:$

$\left[ {0;4} \right].$

$\left[ {5; + \infty } \right).$

$\left( { - \infty ;1} \right).$

$\emptyset .$

Xem đáp án

120

120 lượt xem
Xem đáp án
2 năm trước

Cho các tập hợp: $A = \left\{ {x \in \mathbb{R}|\,x < 3} \right\}{\rm{, }}$ $B = \left\{ {x \in \mathbb{R}|\,1 < x \le 5} \right\}{\rm{,}}$ $C = \left\{ {x \in \mathbb{R}|\, - 2 \le x \le 4} \right\}.$

Tìm $\left( {B \cup C} \right)\backslash \left( {A \cap C} \right)$

Trả lời bởi giáo viên

Câu hỏi khác

Cho hai tập hợp $A = \left[ { - 2;7} \right),{\rm{ }}B = \left( {1;9} \right]$ . Kết quả của phép toán $A \cup B$ là

Cho $A = \left\{ {x \in R:\left| x \right| \le 5} \right\}.$ Phần bù của $A$ trong tập số thực là:

Cho các tập hợp: $A = \left( { - \infty ;3} \right),$ $B = \left\{ {x \in R\left| {x \ge 5} \right.} \right\},$ $C = \left[ {1;7} \right)$ . Tập hợp $A \cap \left( {B \cup C} \right)$ là:

Cho tập hợp $A = \left( {2; + \infty } \right)$ . Khi đó tập ${C_\mathbb{R}}A$ là

Cho tập hợp $A = \left[ { - 2;3} \right],B = \left( {1;5} \right]$ . Khi đó tập $A\backslash B$ là

Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp $A = \left\{ {\left. {x \in \mathbb{R}} \right|4 \le x \le 9} \right\}$ :

Cho $A = \left[ {1;4} \right];B = \left( {2;6} \right);C = \left( {1;2} \right).$ Tìm $A \cap B \cap C:$

Đề thi - đề kiểm tra Xem thêm

Hỏi bài tập Xem thêm

Câu 1. Để chọn toàn bộ văn bản , ta bấm gì ?
A. Ctrl-H
B. Ctrl-A
C. Ctrl-C
D. Ctrl-X
Câu 2. Để di chuyển một vùng sang vị trí khác , ta phải sử dụng cặp phím tắt nào ?
A. Ctrl-A; Ctrl-C
B. Ctrl-C; Ctrl-X
C. Ctrl-X; Ctrl-V
D. Ctrl-V; Ctrl-X

Phân tử CHCl3 có hiệu độ âm điện là bao nhiêu? Giải chi tiết giúp mình nha !!!

Chúng tôi

Học tốt

Liên kết

Mạng xã hội