Các tập hợp số

Tập $\left[ {0;4} \right]$

Tập  $\left[ {0;4} \right] \cap \left[ {3;5} \right]$

Vậy  $\left[ {0;4} \right] \cap \left[ {3;5} \right] = \left[ {3;4} \right]$

Ta có: $\left( { - \infty ; - 2} \right] \cap \left[ { - 2; + \infty } \right) = \left\{ { - 2} \right\}$.

Vì $\left( { - \infty ; - 2} \right]$ tương ứng với: $x\le -2$

$\left[ { - 2; + \infty } \right)$  tương ứng với: $x\ge -2$

$\left( { - \infty ; - 2} \right] \cap \left[ { - 2; + \infty } \right)$ tương ứng với  $x\le -2$ và $x\ge -2$.

Vậy $x=-2$

Xét trục số:

Phần không bị gạch là phần bù của $\left( { - \infty ;4} \right)$, tức là $\left[ {4; + \infty } \right)$

Vậy $\left( {0; + \infty } \right)\backslash \left( { - \infty ;4} \right) = \left[ {4; + \infty } \right)$

Quan sát hình vẽ ta thấy, tập hợp được biểu diễn là tập $\left( { - \infty ; - 3} \right) \cup \left[ {3; + \infty } \right)$ hay $\mathbb{R}\backslash \left[ { - 3;3} \right).$

Ta có: $A = ( - \infty ;2]$,  $B = {\rm{[}}2; + \infty )$, $C = \left( {0;3} \right)$

+) $B \cap C = \left[ {2;3} \right)$ nên A đúng.

+) $A \cap C = (0;2]$ nên B đúng.

+) $A \cup B = R$ nên C sai.

+) $B \cup C = (0; + \infty )$ nên D đúng.

Ta có: $A = \left[ {-2;4} \right),B = \left( {0;{\rm{ }}5} \right]$

Do đó, $A \cup B = \left[ { - 2;5} \right]$ nên A đúng.

+) $A \cap B = \left( {0;4} \right)$ nên B sai.

+) $A\backslash B = \left[ {-2;0} \right]$ nên C đúng.

+) $B\backslash A = \left[ {4;5} \right]$ nên D đúng.

Ta có: $A = \left\{ {x \in R|\left| x \right| > 4} \right\} = \left( { - \infty ; - 4} \right) \cup \left( {4; + \infty } \right)$

$B = \left\{ {x \in R| - 5 \le x - 1 < 5} \right\} = \left[ { - 4;6} \right)$

Khi đó, $A \cup B = \left( { - \infty ; - 4} \right) \cup \left( {4; + \infty } \right) \cup \left[ { - 4;6} \right) = R$

+) $A \cap B = (4;6)$ nên A đúng.

+) $B\backslash A = [ - 4;4]$ nên B đúng.

+) $R\backslash (A \cap B) = \left( { - \infty ;4} \right] \cup \left[ {6; + \infty } \right)$ nên C sai.

+) $R\backslash (A \cup B) = R\backslash R = \emptyset$ nên D đúng.

Vì $\left( {4; + \infty } \right) \cap \left( {-\infty ;2} \right] = \emptyset$ nên $\left( {4; + \infty } \right)\backslash \left( {-\infty ;2} \right] = \left( {4; + \infty } \right)$.

Ta có: $\left( {-\infty ;3} \right) \cup \left[ {3; + \infty } \right) = R$ nên A đúng.

$R\backslash \left( {-\infty ;0} \right) = \left[ {0; + \infty } \right) = {R_ + }$ nên B đúng.

$R\backslash \left( {0; + \infty } \right) = \left( { - \infty ;0} \right] = {R_ - }$ nên C đúng và D sai.

Ta có: $A\backslash B = \emptyset  \Leftrightarrow A \subset B$ hoặc $A = B$.

Đặt $A = \left[ {3;12} \right),B = \left( { - \infty ;a} \right)$

Dễ thấy $A \ne B$ nên bài toán thỏa mãn $\Leftrightarrow A \subset B \Leftrightarrow \left[ {3;12} \right) \subset \left( { - \infty ;a} \right) \Leftrightarrow 12 \le a$.

Ta có: $A = \left[ {a;a + 1} \right) \Rightarrow {C_R}A = R\backslash A = \left( { - \infty ;a} \right) \cup \left[ {a + 1; + \infty } \right)$

Để $\left( { - \infty ;1} \right] \cap \left( {m;m + 1} \right) = \emptyset$ thì hai tập số $\left( { - \infty ;1} \right]$ và $\left( {m;m + 1} \right)$ phải rời nhau trên $R$.

Khi đó tập $\left( {m;m + 1} \right)$ khi biểu diễn trên trục số sẽ phải nằm về bên phải tập $\left( { - \infty ;1} \right]$.

Điều đó chỉ xảy ra khi $1 \le m < m + 1 \Leftrightarrow m \ge 1$.

$\left( {0;1} \right) \cap \left( {m;m + 3} \right) = \emptyset  \Leftrightarrow \left[ \begin{array}{l}0 < 1 \le m < m + 3\\m < m + 3 \le 0 < 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \ge 1\\m \le  - 3\end{array} \right.$.

Ta có: $\left( { - \infty ;0} \right] \cap \left[ {m - 1;m + 1} \right) = A$ với $A$ chỉ có một phần tử

$\Leftrightarrow 0 = m - 1 < m + 1 \Leftrightarrow m = 1$.

Ta có: $\left( { - 1;1} \right) \subset \left( {m;m + 3} \right) \Leftrightarrow m \le  - 1 < 1 \le m + 3 \Leftrightarrow  - 2 \le m \le  - 1$.

+) TH1: $- 1 \le m - 1 \le 1 \Leftrightarrow  0 \le m \le 2$

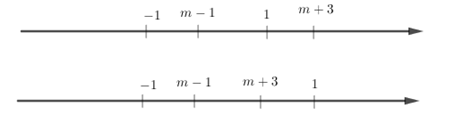
+) TH2: $m - 1 \le  - 1 \le m + 3 \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge  - 4\end{array} \right. \Leftrightarrow  - 4 \le m \le 0$

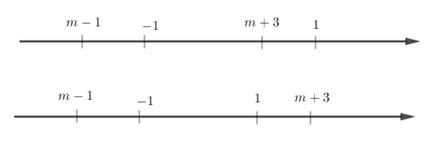
Kết hợp hai trường hợp trên ta được $\left[ \begin{array}{l} 0 \le m \le 2\\ - 4 \le m \le 0\end{array} \right. \Leftrightarrow  - 4 \le m \le 2$

Đặt $B = \left( { - \infty ; - 1} \right),C = \left( {1; + \infty } \right),A = \left[ {a;\dfrac{{a + 1}}{2}} \right]$. Khi đó:

$A \subset \left( {B \cup C} \right) \Leftrightarrow \left[ \begin{array}{l}\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left( { - \infty ; - 1} \right)\\\left[ {a;\dfrac{{a + 1}}{2}} \right] \subset \left( {1; + \infty } \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a \le \dfrac{{a + 1}}{2} <  - 1\\1 < a \le \dfrac{{a + 1}}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2a \le a + 1 <  - 2\\2 < 2a \le a + 1\end{array} \right. \Leftrightarrow a <  - 3$

Xét trục số:

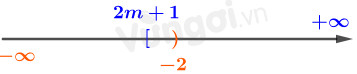
$A \cup B = \mathbb{R} \Leftrightarrow 2m + 1 \le  - 2 \Leftrightarrow m \le \dfrac{{ - 3}}{2}$

Ta có: $\mathbb{R}\backslash \left[ {1;3} \right] = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right).$

Biểu diễn trên trục số: