Câu hỏi:
3 năm trước
Tìm $m$ để \(\left[ { - 1;1} \right] \cap \left[ {m - 1;m + 3} \right] \ne \emptyset \)
Trả lời bởi giáo viên
Đáp án đúng: c
+) TH1: \( - 1 \le m - 1 \le 1 \Leftrightarrow 0 \le m \le 2\)
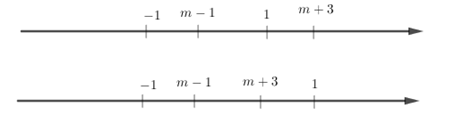
+) TH2: \(m - 1 \le - 1 \le m + 3 \Leftrightarrow \left\{ \begin{array}{l}m \le 0\\m \ge - 4\end{array} \right. \Leftrightarrow - 4 \le m \le 0\)
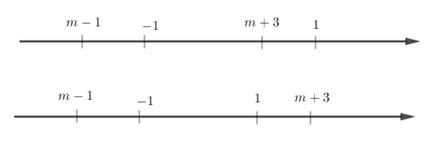
Kết hợp hai trường hợp trên ta được \(\left[ \begin{array}{l} 0 \le m \le 2\\ - 4 \le m \le 0\end{array} \right. \Leftrightarrow - 4 \le m \le 2\)
Hướng dẫn giải:
Liệt kê các trường hợp để hai tập hợp \(\left[ { - 1;1} \right]\) và \(\left[ {m - 1;m + 3} \right]\) có giao khác rỗng (biểu thị trên trục số).

