Phương trình ${x^2} + 3\left| {x - 3} \right| = 2x + 5$ có tích của tất cả các nghiệm nguyên là
Phương trình ${x^2} + 3\left| {x - 3} \right| = 2x + 5$$ \Leftrightarrow 3\left| {x - 3} \right| = 2x + 5 - {x^2}$$\left( * \right)$.
Do $3\left| {x - 3} \right|\ge 0$ nên $2x + 5 - {x^2} \ge 0$ $ \Leftrightarrow 1 - \sqrt 6 \le x \le 1 + \sqrt 6 $.
TH1: $3 \le x \le 1 + \sqrt 6 $.
Phương trình $\left( * \right)$ $ \Leftrightarrow {x^2} + x - 14 = 0$ $ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{ - 1 + \sqrt {57} }}{2}\left( {TM} \right)\\x = \dfrac{{ - 1 - \sqrt {57} }}{2}\left( L \right)\end{array} \right.$.
TH2: $1 - \sqrt 6 \le x < 3$.
Phương trình $\left( * \right)$ $ \Leftrightarrow {x^2} - 5x + 4 = 0$ $ \Leftrightarrow x = 1$ (do $x = 4$ loại).
Phương trình \(\left| {{x^2} + 2x - 3} \right| = x + 5\) có tổng các nghiệm nguyên là
+ Với \(x + 5 < 0 \Leftrightarrow x < - 5\) ta có \({\rm{VT}} \ge 0\), \({\rm{VP}} < 0\) suy ra phương trình vô nghiệm
+ Với \(x + 5 \ge 0 \Leftrightarrow x \ge - 5\)
Phương trình \( \Leftrightarrow \left[ \begin{array}{l}{x^2} + 2x - 3 = x + 5\\{x^2} + 2x - 3 = - x - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} + x - 8 = 0\\{x^2} + 3x + 2 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{ - 1 + \sqrt {33} }}{2}\\x = \dfrac{{ - 1 - \sqrt {33} }}{2}\end{array} \right. (TM) \) hoặc \(\left[ \begin{array}{l}x = - 1\\x = - 2\end{array} \right. (TM)\)
Do đó tổng các nghiệm nguyên là: \( (-2)+(-1)=- 3\)
Có nhiều nhất bao nhiêu số nguyên \(m\) thuộc nửa khoảng \(\left[ { - 2017;2017} \right)\) để phương trình \(\sqrt {2{x^2} - x - 2m} = x - 2\) có nghiệm:
Phương trình đã cho tương đương với: \(\left\{ \begin{array}{l}x \ge 2\\2{x^2} - x - 2m = {x^2} - 4x + 4\end{array} \right.\) $ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} + 3x - 4 = 2m\end{array} \right.$
Xét hàm \(y = {x^2} + 3x - 4\) trên \(\left[ {2; + \infty } \right)\) ta có:
BBT:
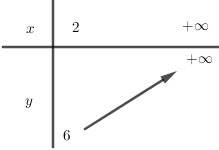
Để phương trình đã cho có nghiệm điều kiện là \(2m \ge 6\) \( \Leftrightarrow m \ge 3\).
Mà \(m \in \left[ { - 2017;2017} \right)\) suy ra \(3 \le m < 2017\).
Vậy có nhiều nhất \(2014\) số nguyên thỏa mãn yêu cầu bài toán.
Một xe hơi khởi hành từ Krông Năng đi đến Nha Trang cách nhau ${\rm{175}}km$. Khi về xe tăng vận tốc trung bình hơn vận tốc trung bình lúc đi là $20$ km/giờ. Biết rằng thời gian dùng để đi và về là \(6\) giờ; vận tốc trung bình lúc đi là
Gọi $x$, $y$ $ > 0$ (km/giờ) lần lượt là vận tốc trung bình lúc đi và vận tốc trung bình lúc về.
Theo đề bài ta có hệ phương trình:
$\left\{ \begin{array}{l}y - x = 20\\\dfrac{{175}}{x} + \dfrac{{175}}{y} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 20 + x\,\,\,\left( 1 \right)\\\dfrac{{175}}{x} + \dfrac{{175}}{y} = 6\,\,\,\left( 2 \right)\end{array} \right.$
Thế $\left( 1 \right)$ vào $\left( 2 \right)$ ta được
$\dfrac{{175}}{x} + \dfrac{{175}}{{20 + x}} = 6$ $ \Leftrightarrow 6{x^2} - 230x - 3500 = 0 $ $\Leftrightarrow \left[ \begin{array}{l}x = 50\\x = - \dfrac{{35}}{3}\end{array} \right. $ $\Rightarrow x = 50$ vì $x > 0$
Vậy vận tốc lúc đi là $50$ km/giờ.
Có bao nhiêu giá trị nguyên của $m$ để phương trình ${x^2} - 2x - 3 - 2m = 0$ có đúng một nghiệm $x \in \left[ {0;4} \right]$.
Ta có ${x^2} - 2x - 3 - 2m = 0$\( \Leftrightarrow {x^2} - 2x - 3 = 2m\).
Để phương trình đã cho có đúng một nghiệm $x \in \left[ {0;4} \right]$ thì đường thẳng \(y = 2m\) cắt đồ thị hàm số \(y = {x^2} - 2x - 3\) trên \(\left[ {0;4} \right]\) tại một điểm duy nhất.
Lập bảng biến thiên của hàm số trên $[0;4]$
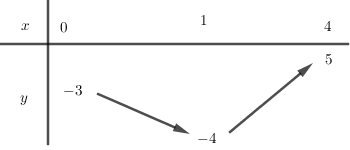
Dựa vào bảng biến thiên ta có:
Để phương trình đã cho có nghiệm duy nhất thuộc $[0;4]$ thì \(\left[ \begin{array}{l}2m = - 4\\ - 3 < 2m \le 5\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}m = - 2\\ - \dfrac{3}{2} < m \le \dfrac{5}{2}\end{array} \right.\)
Vậy các giá trị nguyên của \(m\) thỏa mãn là \(m \in \left\{ { - 2; - 1;0;1;2} \right\}\)
Cho phương trình \({x^3} - \left( {2m + 1} \right){x^2} + \left( {4m - 1} \right)x - 2m + 1 = 0\). Số các giá trị của \(m\) để phương trình có một nghiệm duy nhất?
Tập xác định \(D = \mathbb{R}\).
Phương trình tương đương với \(\left( {x - 1} \right)\left( {{x^2} - 2mx + 2m - 1} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2mx + 2m - 1 = 0\,\,\left( * \right)\end{array} \right.\).
Ta có, phương trình \(\left( * \right)\) có \(\Delta ' = {m^2} - 2m + 1 = {\left( {m - 1} \right)^2} \ge 0\).
Phương trình đã cho có duy nhất một nghiệm nếu phương trình \(\left( * \right)\) có nghiệm kép \(x = 1\)
\( \Rightarrow \Delta ' = 0\) \( \Leftrightarrow m = 1\).
Thay \(m = 1\) vào phương trình \(\left( * \right)\), ta được \({x^2} - 2x + 1 = 0\) \( \Leftrightarrow x = 1\) (thỏa mãn).
Vậy với \(m = 1\) thì phương trình đã cho có một nghiệm duy nhất.
Khi hệ phương trình $\left\{ \begin{array}{l}x + 2my - z = 1\\2x - my - 2z = 2\\x - \left( {m + 4} \right)y - z = 1\end{array} \right.$ có nghiệm $\left( {x;y;z} \right)$ với $\left\{ \begin{array}{l}m \ne 0\\m \ne - \dfrac{4}{3}\end{array} \right.$, giá trị $T = 2017x - 2018y - 2017z$ là
Kí hiệu $\left\{ \begin{array}{l}x + 2my - z = 1 \;\; \left( 1 \right)\\2x - my - 2z = 2 \;\; \left( 2 \right)\\x - \left( {m + 4} \right)y - z = 1 \;\; \left( 3 \right)\end{array} \right.$.
Lấy \(\left( 1 \right) - \left( 3 \right)\) vế với vế ta được \(\left( {3m + 4} \right)y = 0 \Leftrightarrow y = 0\) (do \(m \ne 0; - \dfrac{4}{3}\))
Khi đó \(\left\{ \begin{array}{l}x - z = 1\\y = 0\end{array} \right.\)
Ta có $T = 2017x - 2018y - 2017z$$ = 2017\left( {x - z} \right)$$ = 2017$.
Cho hệ phương trình \(\left\{ \begin{array}{l}{x^2} + 2xy + 8x = 3{y^2} + 12y + 9\\{x^2} + 4y + 18 - 6\sqrt {x + 7} - 2x\sqrt {3y + 1} = 0\end{array} \right.\) có nghiệm là $\left( {a;b} \right)$. Khi đó giá trị biểu thức \(T = 5{a^2} + 4{b^2}\)
Điều kiện \(\left\{ \begin{array}{l}x \ge - 7\\y \ge - \dfrac{1}{3}\end{array} \right.\,\,\,\left( * \right)\)
\(\left\{ \begin{array}{l}{x^2} + 2xy + 8x = 3{y^2} + 12y + 9\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} + 4y + 18 - 6\sqrt {x + 7} - 2x\sqrt {3y + 1} = 0\,\,\,\,\left( 2 \right)\end{array} \right.\)
Có: \(\left( 1 \right) \Leftrightarrow {x^2} + 2\left( {y + 4} \right)x - 3{y^2} - 12y - 9 = 0\), ta coi \(\left( 1 \right)\) là phương trình bậc hai ẩn \(x\) và \(y\) là tham số, giải \(x\) theo \(y\) ta được \(\left[ \begin{array}{l}x = - 3y - 9\\x = y + 1\end{array} \right.\)
Với \(x = - 3y - 9\) thì \(\left( * \right) \Rightarrow \left\{ \begin{array}{l} - 3y - 9 \ge - 7\\y \ge - \dfrac{1}{3}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}y \le - \dfrac{2}{3}\\y \ge - \dfrac{1}{3}\end{array} \right.\) (Vô lý)
Với \(x = y + 1\) $ \Leftrightarrow y = x - 1$ thì
\(\left( 2 \right) \Rightarrow {x^2} + 4x - 6\sqrt {x + 7} - 2x\sqrt {3x - 2} + 14 = 0\) $ \Leftrightarrow \left( {{x^2} - 2x\sqrt {3x - 2} + 3x - 2} \right) + \left( {x + 7 - 6\sqrt {x + 7} + 9} \right) = 0$ \( \Leftrightarrow {\left( {x - \sqrt {3x - 2} } \right)^2} + {\left( {\sqrt {x + 7} - 3} \right)^2} = 0\)
\( \Leftrightarrow \left\{ \begin{array}{l}x = \sqrt {3x - 2} \\\sqrt {x + 7} = 3\end{array} \right.\) \( \Leftrightarrow x = 2\) (thỏa mãn) \( \Rightarrow y = 1\) (thỏa mãn)
Hệ phương trình có nghiệm là \(\left( {2;\,1} \right)\)\( \Rightarrow a = 2\), \(b = 1\) \( \Rightarrow \) \(T = 24\).
Cho biết tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 2m + 1 = 0\) có nghiệm là \(S = \left[ { - \dfrac{a}{b}; + \infty } \right)\), với \(a\), \(b\) là các số nguyên dương và \(\dfrac{a}{b}\) là phân số tối giản. Tính \(T = a + b\).
Điều kiện xác định: $x \ne 0$. Đặt \(t = x + \dfrac{1}{x}\)\( \Rightarrow {t^2} - 2 = {x^2} + \dfrac{1}{{{x^2}}} \ge 2\)\( \Rightarrow \left| t \right| \ge 2\)\( \Leftrightarrow \left[ \begin{array}{l}t \ge 2\\t \le - 2\end{array} \right.\).
Phương trình đã cho trở thành \(2\left( {{t^2} - 2} \right) - 3t - 2m + 1 = 0\)\( \Leftrightarrow 2{t^2} - 3t - 2m - 3 = 0\)
\( \Leftrightarrow 2{t^2} - 3t - 3 = 2m\) (1)
Xét hàm số \(y = f\left( t \right) = 2{t^2} - 3t - 3\) có bảng biến thiên
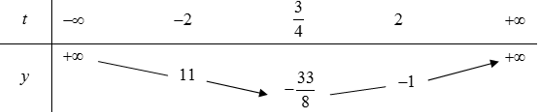
(1) có nghiệm $t$ thỏa \(\left[ \begin{array}{l}t \ge 2\\t \le - 2\end{array} \right.\) khi \(\left[ \begin{array}{l}2m \ge - 1\\2m \ge 11\end{array} \right.\)\( \Leftrightarrow m \ge - \dfrac{1}{2}\)\( \Rightarrow S = \left[ { - \dfrac{1}{2}; + \infty } \right)\).
Vậy \(T = 3\).
Các nghiệm của hệ $\left\{ \begin{array}{l}xy - 3x - 2y = 16\\{x^2} + {y^2} - 2x - 4y = 33\end{array} \right.$ là
Ta có: $\left\{ \begin{array}{l}xy - 3x - 2y = 16\\{x^2} + {y^2} - 2x - 4y = 33\end{array} \right. \left( 1 \right)$
$ \Leftrightarrow \left\{ \begin{array}{l}\left( {xy - 2x - y + 2} \right) - x + 1 - y + 2 = 21\\\left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) = 38\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)\left( {y - 2} \right) - \left( {x - 1} \right) - \left( {y - 2} \right) = 21\\{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 38\end{array} \right. \left( 2 \right)$
Đặt $u = x - 1\,$; $v = y - 2$ ta được hệ $\left\{ \begin{array}{l}uv - \left( {u + v} \right) = 21\\{u^2} + {v^2} = 38\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}uv - \left( {u + v} \right) = 21\\{\left( {u + v} \right)^2} - 2uv = 38\end{array} \right.$
Đặt $S = u + v$; $P = uv$ ta được hệ $\left\{ \begin{array}{l}P - S = 21\\{S^2} - 2P = 38\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}P = S + 21\\{S^2} - 2S - 80 = 0\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}S = - 8\\P = 13\end{array} \right.\,\,$ hoặc $\,\,\left\{ \begin{array}{l}S = 10\\P = 31\end{array} \right.$.
+ Khi $\left\{ \begin{array}{l}S = - 8\\P = 13\end{array} \right.\,\,$ thì $u$; $v$ là nghiệm của phương trình: ${X^2} + 8X + 13 = 0$
$ \Leftrightarrow \left\{ \begin{array}{l}u = - 4 + \sqrt 3 \\v = - 4 - \sqrt 3 \end{array} \right.\,\,\,$ hoặc $\,\,\left\{ \begin{array}{l}u = - 4 - \sqrt 3 \\v = - 4 + \sqrt 3 \end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}x - 1 = - 4 + \sqrt 3 \\y - 2 = - 4 - \sqrt 3 \end{array} \right.\,\,\,\,$ hoặc $\left\{ \begin{array}{l}x - 1 = - 4 - \sqrt 3 \\y - 2 = - 4 + \sqrt 3 \end{array} \right.\,$
$ \Leftrightarrow \left\{ \begin{array}{l}x = - 3 + \sqrt 3 \\y = - 2 - \sqrt 3 \end{array} \right.\,\,\,$ hoặc $\left\{ \begin{array}{l}x = - 3 - \sqrt 3 \\y = - 2 + \sqrt 3 \end{array} \right.$.
+ Khi $\left\{ \begin{array}{l}S = 10\\P = 31\end{array} \right.$ thì $u$; $\,\,v$ là nghiệm của phương trình: ${X^2} - 10X + 31 = 0$ (vô nghiệm)
Vậy hệ có nghiệm \(\left( {x;y} \right) = \left( { - 3 - \sqrt 3 ; - 2 + \sqrt 3 } \right);\) \(\left( {x;y} \right) = \left( { - 3 + \sqrt 3 ; - 2 - \sqrt 3 } \right)\)
Tìm các giá trị của \(m\) để phương trình \(2\sqrt {x + 1} = x + m\) có nghiệm:
\(2\sqrt {x + 1} = x + m\)\(\left( 1 \right)\)
Phương trình tương đương: \(\left\{ \begin{array}{l}x + m \ge 0\\4\left( {x + 1} \right) = {x^2} + 2mx + {m^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge - m\\{x^2} + 2\left( {m - 2} \right)x + {m^2} - 4 = 0\left( 2 \right)\end{array} \right.\)
Phương trình \(\left( 2 \right)\) có nghiệm \( \Leftrightarrow {\rm{pt}}\left( 2 \right)\)có ít nhất một nghiệm lớn hơn hoặc bằng \( - m\).
\(\Delta ' = 8 - 4m\)
Phương trình \(\left( 2 \right)\) có nghiệm \( \Leftrightarrow \Delta ' \ge 0\)\( \Leftrightarrow m \le 2\)
Khi đó phương trình \(\left( 2 \right)\) có hai nghiệm \(\left\{ \begin{array}{l}{x_1} = 2 - m - \sqrt {8 - 4m} \\{x_2} = 2 - m + \sqrt {8 - 4m} \end{array} \right.\).
Dễ thấy \({x_2} = 2 - m + \sqrt {8 - 4m} > - m,\forall m \le 2\) nên \(\left( 2 \right)\) luôn có ít nhất \(1\) nghiệm \(x \ge - m\) thỏa mãn bài toán.
Vậy \(m \le 2\).
Gọi $S$ là tập hợp tất các giá trị thực của tham số $m$ để đường thẳng $\left( d \right):\,y = mx$ cắt parabol $\left( P \right):y = - {x^2} + 2x + 3$ tại hai điểm phân biệt $A$ và $B$ sao cho trung điểm $I$ của đoạn thẳng $AB$ thuộc đường thẳng $\left( \Delta \right):\,y = x - 3$. Tính tổng tất cả các phần tử của $S$.
Phương trình hoành độ giao điểm: $ - {x^2} + 2x + 3 = mx \Leftrightarrow {x^2} + \left( {m - 2} \right)x - 3 = 0\,\,\left( 1 \right)$
Dễ thấy \(\left( 1 \right)\) luôn có \(2\) nghiệm phân biệt vì \(ac = 1.\left( { - 3} \right) = - 3 < 0\)
Khi đó \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\,m{x_1}} \right)\), \(B\left( {{x_2};\,m{x_2}} \right)\), với \({x_1}\), \({x_2}\) là nghiệm phương trình \(\left( 1 \right)\). Theo Viét, có: \({x_1} + {x_2} = 2 - m\), \({x_1}{x_2} = - 3\)
\(I\) là trung điểm \(AB \Rightarrow I = \left( {\dfrac{{{x_1} + {x_2}}}{2};\,\dfrac{{m{x_1} + m{x_2}}}{2}} \right) = \left( {\dfrac{{2 - m}}{2};\,\dfrac{{ - {m^2} + 2m}}{2}} \right)\)
Mà \(I \in \left( \Delta \right):\,y = x - 3 \) \(\Rightarrow \dfrac{{ - {m^2} + 2m}}{2} = \dfrac{{2 - m}}{2} - 3 \) \(\Leftrightarrow {m^2} - 3m - 4 = 0 \) \(\Leftrightarrow \left[ \begin{array}{l}m = - 1 = {m_1}\\m = 4 = {m_2}\end{array} \right.\) \( \Rightarrow {m_1} + {m_2} = 3\).
Cho biết tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 5m + 1 = 0\) có nghiệm là \(S = \left[ { - \dfrac{a}{b}; + \infty } \right)\), với \(a\), \(b\) là các số nguyên dương và \(\dfrac{a}{b}\) là phân số tối giản. Tính $T = a.b$
Đặt \(x + \dfrac{1}{x} = t\), \(\left| t \right| \ge 2\) khi đó phương trình trở thành \(2{t^2} - 3t - 5m - 3 = 0\) (*)
Phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 5m + 1 = 0\) có nghiệm khi và chỉ khi phương trình (*) có nghiệm \(t\) thỏa mãn \(\left| t \right| \ge 2\).
Số nghiệm của phương trình (*) bằng số giao điểm của parabol \(\left( P \right):y = 2{t^2} - 3t - 3\) và đường thẳng \(d:y = 5m\).
Xét parabol \(\left( P \right):y = 2{t^2} - 3t - 3\) ta có bảng biến thiên như sau
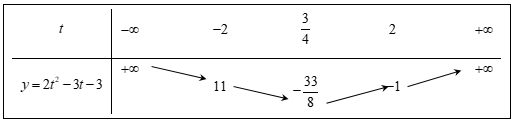
Từ bảng biến thiên ta có phương trình (*) có nghiệm $t \in \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)$ khi và chỉ khi \(5m \ge - 1\) hoặc $5m\ge 11$
\( \Leftrightarrow m \ge - \dfrac{1}{5}\) hoặc $m \ge \dfrac{11}{5} $
\( \Leftrightarrow m \ge - \dfrac{1}{5}\)
Vậy khi \(m \in \left[ { - \dfrac{1}{5}; + \infty } \right)\) thì phương trình có nghiệm \( \Rightarrow \left\{ \begin{array}{l}a = 1\\b = 5\end{array} \right.\) \( \Rightarrow T = 5\).
Cho $\left( {x;y} \right)$ với \(x\), \(y\) nguyên là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{xy + {y^2} + x = 7y\left( 1 \right)}\\{\dfrac{{{x^2}}}{y} + x = 12{\rm{ }}\left( 2 \right)}\end{array}} \right.\) thì tích $xy$ bằng
Điều kiện \(y \ne 0\).
Hệ phương trình tương đương với \(\left\{ {\begin{array}{*{20}{c}}{x + y + \dfrac{x}{y} = 7 \left( 1 \right)}\\{x\left( {\dfrac{x}{y} + 1} \right) = 12 \left( 2 \right)}\end{array}} \right.\)
Từ \(\left( 1 \right)\) và \(x\), \(y\) là số nguyên nên \(y\) là ước của \(x\).
Từ \(\left( 2 \right)\) ta có \(x\) là ước của \(12\).
+ \(x = \pm 1\) thì \(\dfrac{{ \pm 1}}{y} + 1 = \pm 12\) (loại).
+ \(x = \pm 2\) thì \(\dfrac{{ \pm 2}}{y} + 1 = \pm 6\) (loại).
+ \(x = 3\) thì \(\dfrac{3}{y} + 1 = 4\)\( \Leftrightarrow y = 1\) (thỏa mãn) \( \Rightarrow xy = 3\).
+ \(x = - 3\) thì \( - \dfrac{3}{y} + 1 = - 4\) (loại)
+ \(x = 4\) thì \(\dfrac{4}{y} + 1 = 3\Leftrightarrow y = 2\) (loại vì không thỏa mãn \(( 1 )\).
+ $x = - 4$ thì \( - \dfrac{4}{y} + 1 = - 3\) \( \Leftrightarrow y = 1\) (loại vì không thỏa mãn \(\left( 1 \right)\)).
+ \(x = 6\) thì \(\dfrac{6}{y} + 1 = 2\)\( \Leftrightarrow y = 6\) (loại vì không thỏa mãn \(\left( 1 \right)\)).
+ \(x = - 6\) thì \( - \dfrac{6}{y} + 1 = - 2\)\( \Leftrightarrow y = 2\) (loại vì không thỏa mãn \(\left( 1 \right)\)).
+ \(x = 12\) thì \(\dfrac{{12}}{y} + 1 = 1\) vô nghiệm.
+ \(x = - 12\) thì \( - \dfrac{{12}}{y} + 1 = - 1\)\( \Leftrightarrow y = 6\) (loại vì không thỏa mãn \(\left( 1 \right)\)).
Vậy có duy nhất một nghiệm nguyên \(x = 3\); \(y = 1\) nên \(xy = 3\).
Có bao nhiêu giá trị \(m\) nguyên dương để hệ phương trình $\left\{ \begin{array}{l}mx - y = 3\\2x + my = 9\end{array} \right.$ có nghiệm duy nhất \(\left( {x;y} \right)\) sao cho biểu thức \(A = 3x - y\) nhận giá trị nguyên
Ta có \(D = \left| {\begin{array}{*{20}{c}}m&{ - 1}\\2&m\end{array}} \right| = {m^2} + 2 > 0\), \(\forall m \in \mathbb{R}\) nên hệ phương trình luôn có nghiệm duy nhất.
\({D_x} = \left| {\begin{array}{*{20}{c}}3&{ - 1}\\9&m\end{array}} \right| = 3m + 9\); \({D_y} = \left| {\begin{array}{*{20}{c}}m&3\\2&9\end{array}} \right| = 9m - 6\).
Vậy hệ luôn có nghiệm duy nhất là \(\left\{ \begin{array}{l}x = \dfrac{{3m + 9}}{{{m^2} + 2}}\\y = \dfrac{{9m - 6}}{{{m^2} + 2}}\end{array} \right.\).
Ta có \(A = 3x - y\)\( = \dfrac{{3\left( {3m + 9} \right)}}{{{m^2} + 2}} - \dfrac{{9m - 6}}{{{m^2} + 2}}\)\( = \dfrac{{33}}{{{m^2} + 2}}\).
Vì $m \in \mathbb{Z}$ nên để \(A\) nguyên thì \({m^2} + 2\) là ước của \(33\) mà \({m^2} + 2 \ge 2\) nên ta có các trường hợp sau:
+ TH1: \({m^2} + 2 = 3\)\( \Leftrightarrow m = \pm 1\).
+ TH2: \({m^2} + 2 = 11\)\( \Leftrightarrow m = \pm 3\).
+ TH3: \({m^2} + 2 = 33\)\( \Leftrightarrow m = \pm \sqrt {31} \) (loại).
Mà $m$ nguyên dương nên $m \in \{1;3\}$
Vậy có \(2\) giá trị nguyên dương của \(m\) để \(A\) nguyên.

