Câu hỏi:
2 năm trước
Cho biết tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 5m + 1 = 0\) có nghiệm là \(S = \left[ { - \dfrac{a}{b}; + \infty } \right)\), với \(a\), \(b\) là các số nguyên dương và \(\dfrac{a}{b}\) là phân số tối giản. Tính $T = a.b$
Trả lời bởi giáo viên
Đáp án đúng: b
Đặt \(x + \dfrac{1}{x} = t\), \(\left| t \right| \ge 2\) khi đó phương trình trở thành \(2{t^2} - 3t - 5m - 3 = 0\) (*)
Phương trình \(2\left( {{x^2} + \dfrac{1}{{{x^2}}}} \right) - 3\left( {x + \dfrac{1}{x}} \right) - 5m + 1 = 0\) có nghiệm khi và chỉ khi phương trình (*) có nghiệm \(t\) thỏa mãn \(\left| t \right| \ge 2\).
Số nghiệm của phương trình (*) bằng số giao điểm của parabol \(\left( P \right):y = 2{t^2} - 3t - 3\) và đường thẳng \(d:y = 5m\).
Xét parabol \(\left( P \right):y = 2{t^2} - 3t - 3\) ta có bảng biến thiên như sau
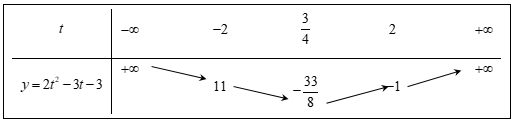
Từ bảng biến thiên ta có phương trình (*) có nghiệm $t \in \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)$ khi và chỉ khi \(5m \ge - 1\) hoặc $5m\ge 11$
\( \Leftrightarrow m \ge - \dfrac{1}{5}\) hoặc $m \ge \dfrac{11}{5} $
\( \Leftrightarrow m \ge - \dfrac{1}{5}\)
Vậy khi \(m \in \left[ { - \dfrac{1}{5}; + \infty } \right)\) thì phương trình có nghiệm \( \Rightarrow \left\{ \begin{array}{l}a = 1\\b = 5\end{array} \right.\) \( \Rightarrow T = 5\).
Hướng dẫn giải:
- Đặt \(x + \dfrac{1}{x} = t\) biến đổi phương trình về ẩn \(t\)
- Sử dụng phương pháp hàm số tìm điều kiện để phương trình mới có nghiệm tương đương với điều kiện bài cho ban đầu.
Câu hỏi khác
- Bài tập đại cương về phương trình toán 10 có lời giải
- Bài tập phương trình bậc nhất và bậc hai một ẩn toán 10 có lời giải
- Bài tập phương trình bậc ba, bậc bốn quy về bậc nhất, bậc hai toán 10 có lời giải
- Bài tập phương trình chứa dấu giá trị tuyệt đối toán 10 có lời giải
- Bài tập phương trình chứa căn toán 10 có lời giải
