Có nhiều nhất bao nhiêu số nguyên \(m\) thuộc nửa khoảng \(\left[ { - 2017;2017} \right)\) để phương trình \(\sqrt {2{x^2} - x - 2m} = x - 2\) có nghiệm:
Trả lời bởi giáo viên
Phương trình đã cho tương đương với: \(\left\{ \begin{array}{l}x \ge 2\\2{x^2} - x - 2m = {x^2} - 4x + 4\end{array} \right.\) $ \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\{x^2} + 3x - 4 = 2m\end{array} \right.$
Xét hàm \(y = {x^2} + 3x - 4\) trên \(\left[ {2; + \infty } \right)\) ta có:
BBT:
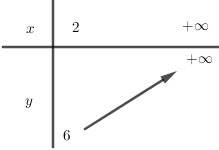
Để phương trình đã cho có nghiệm điều kiện là \(2m \ge 6\) \( \Leftrightarrow m \ge 3\).
Mà \(m \in \left[ { - 2017;2017} \right)\) suy ra \(3 \le m < 2017\).
Vậy có nhiều nhất \(2014\) số nguyên thỏa mãn yêu cầu bài toán.
Hướng dẫn giải:
Phương trình \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {g^2}\left( x \right)\end{array} \right.\)

